3.4乘法公式（1）

七 年级（下）数学课堂探究案
课题 3.4乘法公式（一） 主备 审核 姓名
目标 利用图形的面积推导平方差公式会运用平方差公式进行多项式的乘法运算及简便运算
重点 平方差公式
难点 数形结合解释平方差公式用公式结构特征判断题目能否用平方差公式
学习过程 学习札记
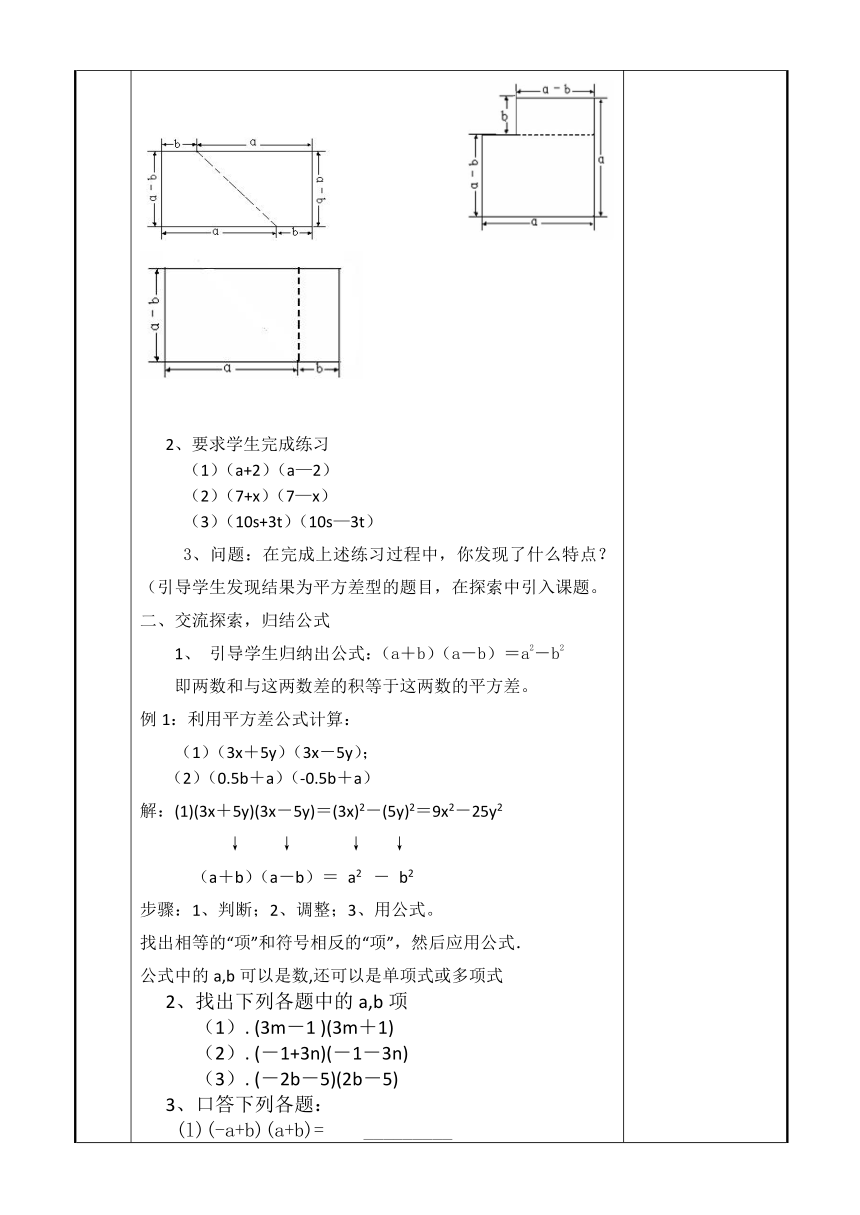
自主探究 创设情境，探究新知 1、将一个边长为a的正方形硬纸片，从中剪去一个边长为b的正方形， （1）请表示出剩余部分的面积；（2）你能将剩余的图形剪成两部分然后拼写一个长方形吗？（3）若能，则所得的这个长方形长和宽分别是多少？面积表示为多少？（4）比较（2）和（1）结果，你能得到怎样的代数关系式？生四人小组合作方式动手操作讨论交流，哪组能派个代表上来演示作个汇报？全班交流： 要求学生完成练习 （1）（a+2）（a—2） （2）（7+x）（7—x） （3）（10s+3t）（10s—3t） 3、问题：在完成上述练习过程中，你发现了什么特点？（引导学生发现结果为平方差型的题目，在探索中引入课题。二、交流探索，归结公式1、 引导学生归纳出公式：（a＋b）（a－b）＝a2－b2即两数和与这两数差的积等于这两数的平方差。例1：利用平方差公式计算：（1）（3x＋5y）（3x－5y）；（2）（0.5b＋a）（-0.5b＋a）解：(1)(3x＋5y)(3x－5y)＝(3x)2－(5y)2＝9x2－25y2↓ ↓ ↓ ↓（a＋b）（a－b）＝ a2 － b2步骤：1、判断；2、调整；3、用公式。找出相等的“项”和符号相反的“项”，然后应用公式． 公式中的a,b可以是数,还可以是单项式或多项式2、找出下列各题中的a,b项　 （1）. (3m－1 )(3m＋1) （2）. (－1+3n)(－1－3n) （3）. (－2b－5)(2b－5)3、口答下列各题： (l)(-a+b)(a+b)= _________ (2)(a-b)(b+a)= __________ (3)(-a-b)(-a+b)= ________ (4)(a-b)(-a-b)= _________ 4、下列式子可用平方差公式计算吗 为什么 如果能够，怎样计算 （1）(a+b)( a b) ； (2) (a b)(b a) ; (3) (a+2b)(2b+a); (4) (a b)(a+b) ; (5) ( 2x+y)(y 2x)例2 用平方差公式计算（1）103×97 （2）59.8×60.2解：（1）103×97＝（100＋3）（100－3）＝1002－32＝10000－9＝9991（2）59.8×60.2＝（60－0.2）（60＋0.2）＝602－0.22＝3600－0.04＝3599.96
课堂小结 谈一谈这节课你的收获与体会
课堂检测 练习运用平方差公式进行计算: （1）1.02*0.98 （2)400.01*399.9 (3)99*101*10001 (4)20062－2007*2005
课后拓展 1、你能很快计算下列式子吗 (结果可用幂的形式表示) （2+1）（22+1）（24+1）（28+1）+12、如果A=1234567892，B=123456788×123456790试比较A与B的大小
教后反思
批改记录