泸教版(2019) 必修1 第1单元项目二 探究计算机中的数据表示 课件(共19张PPT)
文档属性
| 名称 | 泸教版(2019) 必修1 第1单元项目二 探究计算机中的数据表示 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 23.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-11-06 21:22:34 | ||
图片预览






文档简介
(共19张PPT)
项目二探究计算机中的数据表示
认识数据编码
生活中的编码实例
2130198
一级区域编码
二级区域编码
树木编码
思考:如果2区11子区有10026棵树,以上的编码规矩是否适用?
考生类别
农村应届
正确V
京AF0236
网上报名序号
225111604392
网上报名序号为12位!填
学籍号*
学籍号不能为空:
姓名
张胜男
姓名为中文:
身份证号“
120225199510296160
身份证号为18位:
6
937147"252044
编码:指用预先规定的方法将文字、数字或其他对象转换成规定的符号组合。
编码位数与编码可表示情况之间的关系
问题:·(1)1位十进制数能表示多少种情况?2位、3位十进制数呢?
1位:0-9
10种
2位:0-99
100种
3位:0-999
1000种
(2)n位十进制数能表示多少种情况?
10的n次方种
编码体验
任务:以小组为单位,完成活动2.1:了解生活中的编码。活动时间:8分钟
鉴别
编码一般具备的功能和意义
排序
专用含义
了解数制
任务:自学课本20页数制的知识。
数码:组成该数制的基本数字。
数制
数码
基数
十进制
0~9
10
数制的基本要素
基数:组成该数制的数码个数。
二进制
0、1
2
八进制
0~7
8
位权:每一个数位上的1对应的单位值。
十六进
0~9、A、B、
16
制
C、D、E、F
了解数制
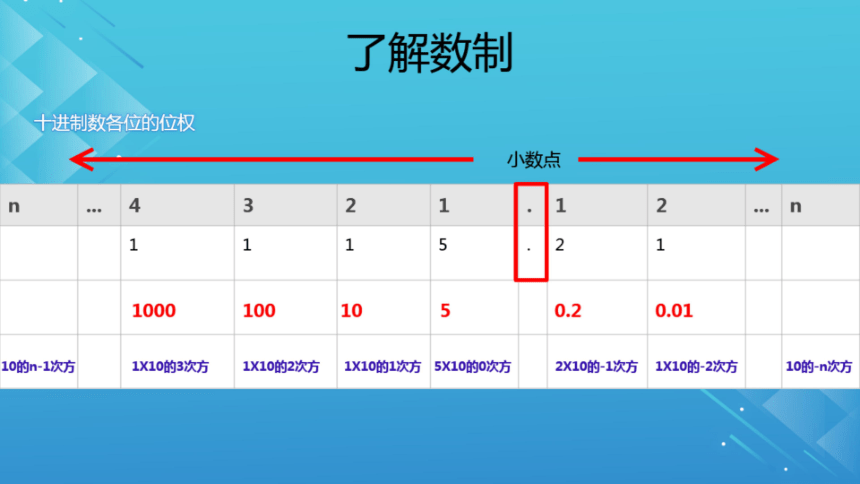
十进制数各位的位权
小数点
n
3
2
1
●
2
000
n
1
1
1
5
2
1
1000
100
10
5
0.2
0.01
10的n-1次方
1X10的3次方
1X10的2次方
1X10的1次方
5X10的0次方
2X10的-1次方
1X10的-2次方
10的-n次方
了解数制
数制
基数
数码
位权规律
后缀
整数
小数
十进制
10
0~9
10的n-1次方
10的-n次方
D
二进制
2
0、1
2的n-1次方
2的-n次方
B
八进制
8
0~7
8的n-1次方
8的-n次方
十六进制
16
09、A、B、C、
H
D、E、F
16的n-1次方
16的-n次方
了解数值数据的编码
任务:阅读课本21页数值数据的编码。
转换
编码
数值数据
二进制数
0、1代码
八、十、十六等
机器语言
十进制转二进制
36.375
=100100.011
1整数部分:除2反向取余法
2.小数部分:乘2正向取整法
236
0.375
218
X2
.0
2L9
0
0.750
14
X2
2
1.500
2
2
X2
2
1
1.000
0
(36)10=(100100)2
(0.375)10=(0.011)2
练习1:请将下面几个十进制数转换成二进制数。填写至任务单中。5.75、50.5
项目二探究计算机中的数据表示
认识数据编码
生活中的编码实例
2130198
一级区域编码
二级区域编码
树木编码
思考:如果2区11子区有10026棵树,以上的编码规矩是否适用?
考生类别
农村应届
正确V
京AF0236
网上报名序号
225111604392
网上报名序号为12位!填
学籍号*
学籍号不能为空:
姓名
张胜男
姓名为中文:
身份证号“
120225199510296160
身份证号为18位:
6
937147"252044
编码:指用预先规定的方法将文字、数字或其他对象转换成规定的符号组合。
编码位数与编码可表示情况之间的关系
问题:·(1)1位十进制数能表示多少种情况?2位、3位十进制数呢?
1位:0-9
10种
2位:0-99
100种
3位:0-999
1000种
(2)n位十进制数能表示多少种情况?
10的n次方种
编码体验
任务:以小组为单位,完成活动2.1:了解生活中的编码。活动时间:8分钟
鉴别
编码一般具备的功能和意义
排序
专用含义
了解数制
任务:自学课本20页数制的知识。
数码:组成该数制的基本数字。
数制
数码
基数
十进制
0~9
10
数制的基本要素
基数:组成该数制的数码个数。
二进制
0、1
2
八进制
0~7
8
位权:每一个数位上的1对应的单位值。
十六进
0~9、A、B、
16
制
C、D、E、F
了解数制
十进制数各位的位权
小数点
n
3
2
1
●
2
000
n
1
1
1
5
2
1
1000
100
10
5
0.2
0.01
10的n-1次方
1X10的3次方
1X10的2次方
1X10的1次方
5X10的0次方
2X10的-1次方
1X10的-2次方
10的-n次方
了解数制
数制
基数
数码
位权规律
后缀
整数
小数
十进制
10
0~9
10的n-1次方
10的-n次方
D
二进制
2
0、1
2的n-1次方
2的-n次方
B
八进制
8
0~7
8的n-1次方
8的-n次方
十六进制
16
09、A、B、C、
H
D、E、F
16的n-1次方
16的-n次方
了解数值数据的编码
任务:阅读课本21页数值数据的编码。
转换
编码
数值数据
二进制数
0、1代码
八、十、十六等
机器语言
十进制转二进制
36.375
=100100.011
1整数部分:除2反向取余法
2.小数部分:乘2正向取整法
236
0.375
218
X2
.0
2L9
0
0.750
14
X2
2
1.500
2
2
X2
2
1
1.000
0
(36)10=(100100)2
(0.375)10=(0.011)2
练习1:请将下面几个十进制数转换成二进制数。填写至任务单中。5.75、50.5
同课章节目录
- 第一单元 数据与信息
- 项目一 探秘鸟类研究——认识数据、信息与知识
- 项目二 探究计算机中的数据表示——认识数据编码
- 单元挑战 认识并制作二维码
- 第二单元 数据处理与应用
- 项目三 调查中学生移动学习现状——经历数据处理的一般过程
- 项目四 认识智能停车场中的数据处理——体验数据处理的方法和工具
- 单元挑战 采集与分析气象数据
- 第三单元 算法和程序设计
- 项目五 描述洗衣机的洗衣流程——了解算法及其基本控制结构
- 项目六 解决温标转换问题——认识程序和程序设计语言
- 项目七 用计算机计算圆周率——设计简单数值数据算法
- 项目八 分析历史气温数据——设计批量数据算法
- 单元挑战 探究密码安全问题
- 第四单元 人工智能初步
- 项目九 了解手写数字识别——体验人工智能
- 单元挑战 尝试人工智能绘画
