全等三角形的复习课[下学期]

全等三角形的复习课
一、教学目标:
1、了解全等形、全等三角形的概念和性质；
2、能够辨认全等三角形中对应的元素；
3、会正确使用全等符号“≌”标注两个三角形全等；
4、能灵活运用“SAS”、“ASA”、“AAS”、 “SSS”来判定三角形全等；
5、会用三角形全等的条件推理和计算有关问题。
二、教学重点：能够辨认全等三角形中对应的元素；能灵活运用“SAS”、“ASA”、“AAS”、 “SSS”来判定三角形全等；
教学难点：在直观认识和操作活动的基础上，运用自己的语言表达，发展推理能力。
三、教学用具：两个全等三角形纸片，课件
四、教学过程设计：
1、引入：
故事：小A和小B是一对双胞胎，两个人都非常喜欢数学——小A认为数学是一种思维体操，小B认为数学能帮助大家解决很多问题。现在，到了期末迎考阶段，两个人不约而同想到了——复习——温故而知新，可以为师矣。妈妈为了鼓励他们，同时表示自己不偏心，在两张重叠的纸上画了一个三角形，并剪下来送给他们俩。
问题：为什么这样做能表示妈妈不偏心？——因为这两个三角形是全等三角形。
问题：你怎么知道这两个三角形是全等三角形？——能够重合的两个三角形是全等三角形。
问题：如果两个三角形是全等三角形，那么它们的对应边相等，对应角也相等。
故事：于是，为了不辜负妈妈，小A和小B开始了对全等三角形的复习。下面，让我们同这对双胞胎兄弟一起来复习全等三角形。
2、能够辨认全等三角形中对应的元素——拼一拼，摆一摆
故事：小A把两个全等三角形三角形纸片按如图方式，拼接在一起，得到图形①，请小B指出这两个全等三角形的对应边和对应角。这个问题对小B来说不费吹灰之力。同学们，你们能否解答呢？——
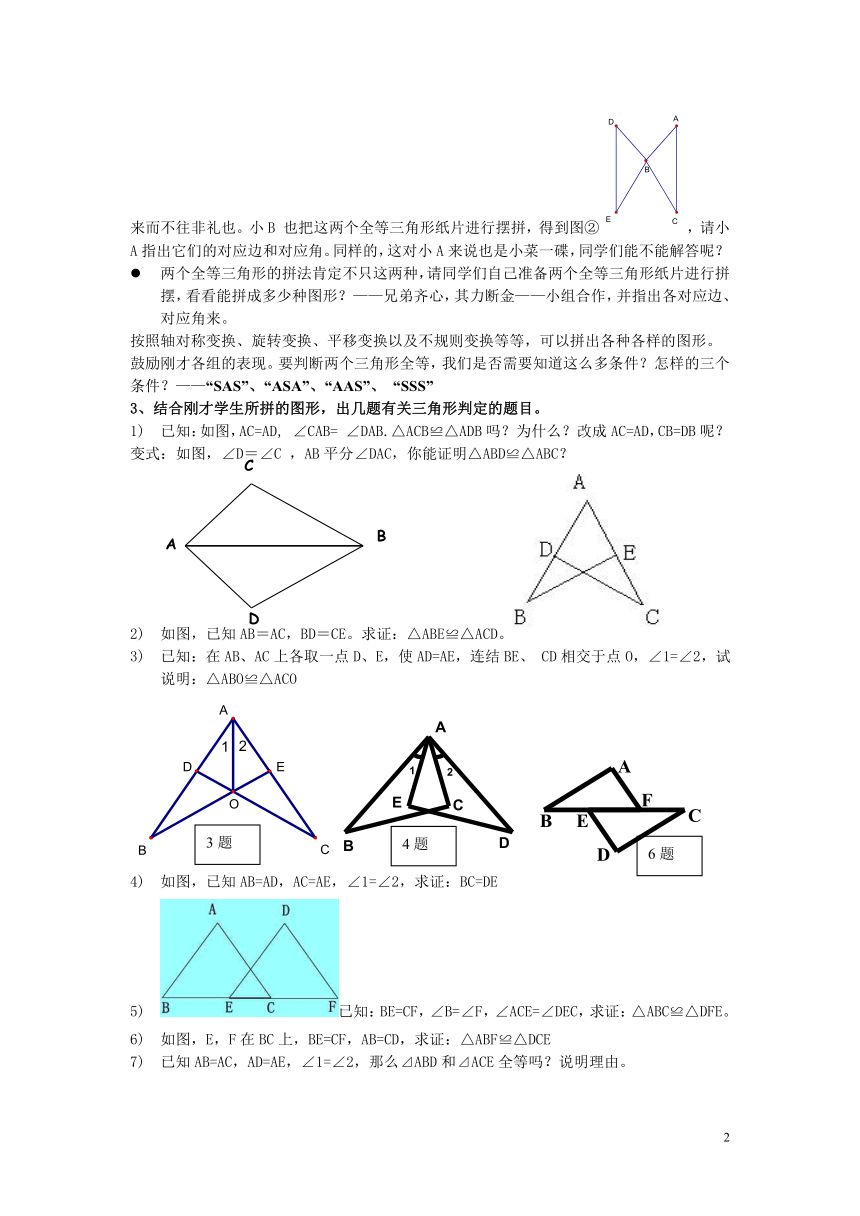
来而不往非礼也。小B 也把这两个全等三角形纸片进行摆拼，得到图②，请小A指出它们的对应边和对应角。同样的，这对小A来说也是小菜一碟，同学们能不能解答呢？
两个全等三角形的拼法肯定不只这两种，请同学们自己准备两个全等三角形纸片进行拼摆，看看能拼成多少种图形？——兄弟齐心，其力断金——小组合作，并指出各对应边、对应角来。
按照轴对称变换、旋转变换、平移变换以及不规则变换等等，可以拼出各种各样的图形。
鼓励刚才各组的表现。要判断两个三角形全等，我们是否需要知道这么多条件？怎样的三个条件？——“SAS”、“ASA”、“AAS”、 “SSS”
3、结合刚才学生所拼的图形，出几题有关三角形判定的题目。
1) 已知：如图，AC=AD, ∠CAB= ∠DAB.△ACB≌△ADB吗？为什么？改成AC=AD，CB=DB呢？
变式：如图，∠D＝∠C ，AB平分∠DAC，你能证明△ABD≌△ABC？
2) 如图，已知AB＝AC，BD＝CE。求证：△ABE≌△ACD。
3) 已知：在AB、AC上各取一点D、E，使AD=AE，连结BE、 CD相交于点O，∠1=∠2，试说明：△ABO≌△ACO
4) 如图，已知AB=AD，AC=AE，∠1=∠2，求证：BC=DE
5) 已知：BE=CF，∠B=∠F，∠ACE=∠DEC，求证：△ABC≌△DFE。
6) 如图，E，F在BC上，BE=CF，AB=CD，求证：△ABF≌△DCE
7) 已知AB=AC，AD=AE，∠1=∠2，那么⊿ABD和⊿ACE全等吗？说明理由。
小结：
三角形全等书写格式：
一、先证明还未知的条件；
二、在△ 与△ 中，
∵ 条件（1）
条件（2）
条件（3）
∴ △ ≌△ （ ）
三角形全等的基本方法
4、妈妈对小A和小B的复习表现非成满意，最后妈妈提出了应用才是硬道理。
某铁路施工队要打通一座小山建隧道，如图，设计时要测隧道的长度，恰好山前是一片空地，利用这样有利地形，测量人员是否可以利用三角形全等的知识测量出隧道长度，画出你设计的测量方法图，并说明理由。
思考：我军在前进途中被大河挡住去路如图，当时部队没有任何测量工具，一战士仅用头上戴的军帽和一条绳子测得了河宽，使部队顺利架起浮桥。
教学反思：
缺点：本课容量过大，在把第3、6题去掉之后，就有了让学生进行书写练习的时间，这样使得本课的节奏不那么快，使学生不至于一节课的时间都在不停的思考，以至于没有喘息的时间。因此也就使得本课的复习效果更好。
优点：本课设计思路清晰，层次感较强。引入比较有意思，过度语言比较自然流畅。
D
B
C
A
2
1
C
E
D
B
A
F
2
1
E
D
C
B
A
E
D
C
B
A
3题
4题
6题
E
D
C
B
A
C
PAGE
4