4.3解二元一次方程组(1)[下学期]
文档属性
| 名称 | 4.3解二元一次方程组(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 426.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-27 13:18:00 | ||
图片预览




文档简介
课件13张PPT。§4.3解二元一次方程组泰六中我国古代数学名著<孙子算经>上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几头?解:设有x只鸡,有y只兔
依题意可得:
X+y=35
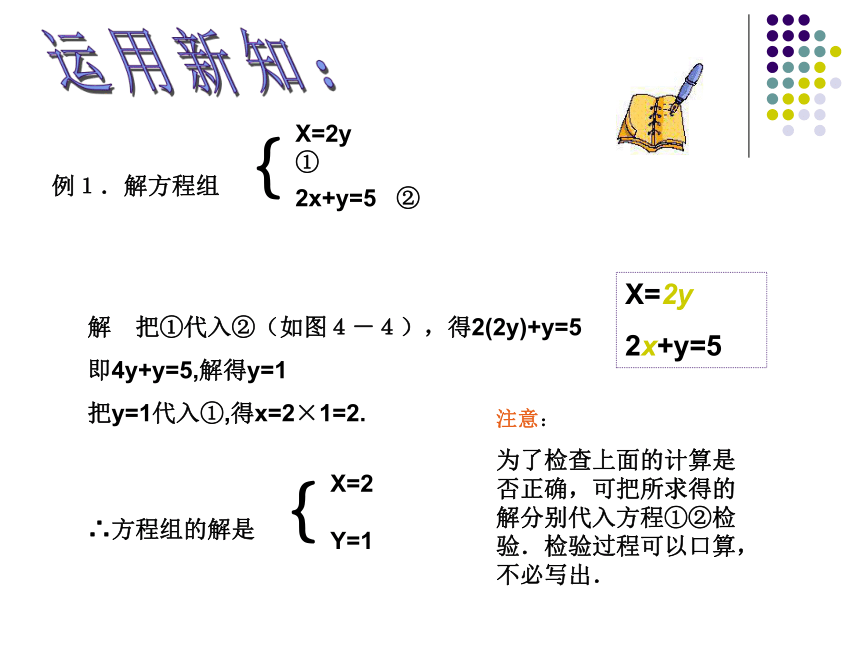
2x+4y=94{这是一个二元一次方程组,怎样解这个方程组呢?“曹冲称象”的故事告诉我们一个什么数学道理?你得到什么启发?合作学习我们已经学过一元一次方程的解法,能否把解二元一次方程转化为解一元一次方程?请观察下图,你又能得到什么启发?yxyX+10X+10200g200g梨换成苹果{xY=x+10 ,
用x+10代替y x+(x+10)=200
X+y=200 消元 (一元)
(二元) 。 上面解方程组的基本思路是“消元”,也就是把二元一次方程组化为一元一次方程。消元的方法是“代入”,这种解方程的方法称为代入消元法,简称代入法 。
代入法是解二元一次方程组常用的方法之一。总结概念:例1.解方程组{ X=2y ①2x+y=5 ②解 把①代入②(如图4-4),得2(2y)+y=5
即4y+y=5,解得y=1
把y=1代入①,得x=2×1=2.
∴方程组的解是{X=2
Y=1X=2y
2x+y=5注意:
为了检查上面的计算是否正确,可把所求得的解分别代入方程①②检验.检验过程可以口算,不必写出.运用新知:小试牛刀:
( 1 ) {X=y+4
5x=3y(2) {X-4y=6
x+2y=12(3) {2x+y=2
3x+2y-5=0x=-6
y=-10x=10
y=1x=-1
y=4{{{例2解方程组{2x-7y=8 ①
3x-8y-10=0 ②提示:将其中一个方程的一个未知数用另一个未知数表示时,通常我们选择的方程应使运算比较简便.解 由 ① ,得2x=8+7y,即x= (8+7y) / 2 ③
把③代入②,得3×<(8+7y)/2 >-8y-10=0
∴12+(21∕2)y-8y-10=0,解得y=-4∕5
把y=-4∕5代入③,得x=<8+7×(-4∕5)> ∕2=6∕5
∴方程组的解是{X= 6∕5
y=-4∕5
用代入法解二元一次方程组的一般步骤是:
1.将方程组中的一个方程变形,使得一个未知数能用含有另一个未知数的代数式表示;
2.用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3.把这个未知数的值代入代数式,求得另一个未知数的值;
4.写出方程组的解.用代入法解下列方程组:
(1){ (2){
(3){ (4){X=1.5y
x+0.5y=2a+b=3
3a-b=5
5x=3y
X-y=43x-4(x-y)=2
2x-3y=1a=2
b=1x=-6
y=-10x=1.5
y=1x=2
y=1{{{{思考题:
已知{ 和{ 是方程ax+by=15的两个解,求的a,b值.X=2
Y=5X=1
Y=10谈谈今天的收获!今天作业:
作业本 课本内作业题(2) 预习再见!
依题意可得:
X+y=35
2x+4y=94{这是一个二元一次方程组,怎样解这个方程组呢?“曹冲称象”的故事告诉我们一个什么数学道理?你得到什么启发?合作学习我们已经学过一元一次方程的解法,能否把解二元一次方程转化为解一元一次方程?请观察下图,你又能得到什么启发?yxyX+10X+10200g200g梨换成苹果{xY=x+10 ,
用x+10代替y x+(x+10)=200
X+y=200 消元 (一元)
(二元) 。 上面解方程组的基本思路是“消元”,也就是把二元一次方程组化为一元一次方程。消元的方法是“代入”,这种解方程的方法称为代入消元法,简称代入法 。
代入法是解二元一次方程组常用的方法之一。总结概念:例1.解方程组{ X=2y ①2x+y=5 ②解 把①代入②(如图4-4),得2(2y)+y=5
即4y+y=5,解得y=1
把y=1代入①,得x=2×1=2.
∴方程组的解是{X=2
Y=1X=2y
2x+y=5注意:
为了检查上面的计算是否正确,可把所求得的解分别代入方程①②检验.检验过程可以口算,不必写出.运用新知:小试牛刀:
( 1 ) {X=y+4
5x=3y(2) {X-4y=6
x+2y=12(3) {2x+y=2
3x+2y-5=0x=-6
y=-10x=10
y=1x=-1
y=4{{{例2解方程组{2x-7y=8 ①
3x-8y-10=0 ②提示:将其中一个方程的一个未知数用另一个未知数表示时,通常我们选择的方程应使运算比较简便.解 由 ① ,得2x=8+7y,即x= (8+7y) / 2 ③
把③代入②,得3×<(8+7y)/2 >-8y-10=0
∴12+(21∕2)y-8y-10=0,解得y=-4∕5
把y=-4∕5代入③,得x=<8+7×(-4∕5)> ∕2=6∕5
∴方程组的解是{X= 6∕5
y=-4∕5
用代入法解二元一次方程组的一般步骤是:
1.将方程组中的一个方程变形,使得一个未知数能用含有另一个未知数的代数式表示;
2.用这个代数式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3.把这个未知数的值代入代数式,求得另一个未知数的值;
4.写出方程组的解.用代入法解下列方程组:
(1){ (2){
(3){ (4){X=1.5y
x+0.5y=2a+b=3
3a-b=5
5x=3y
X-y=43x-4(x-y)=2
2x-3y=1a=2
b=1x=-6
y=-10x=1.5
y=1x=2
y=1{{{{思考题:
已知{ 和{ 是方程ax+by=15的两个解,求的a,b值.X=2
Y=5X=1
Y=10谈谈今天的收获!今天作业:
作业本 课本内作业题(2) 预习再见!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
