6.2提取公因式[下学期]

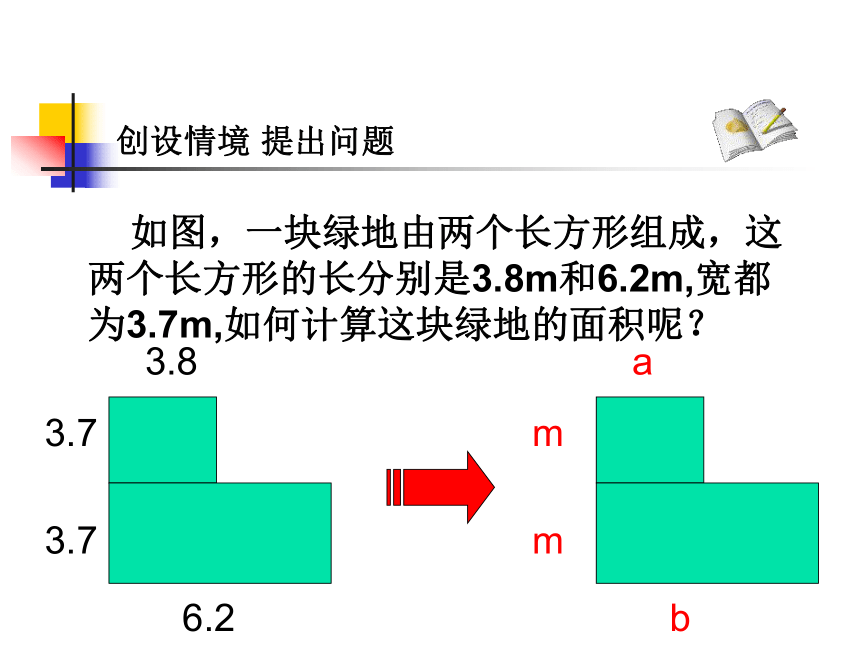
课件17张PPT。6.2提取公因式法因式分解方法之一：七年级数学备课组创设情境 提出问题 如图，一块绿地由两个长方形组成，这两个长方形的长分别是3.8m和6.2m,宽都为3.7m,如何计算这块绿地的面积呢？请找出下式的公因式:3ax2y+6x3yz
ma+ mb =m( a+b ) 一个多项式每一项都含有的相同的因式，叫做这个多项式各项的公因式。把一个多项式的公因式提取出来进行因式分解，这种分解因式的方法叫做提取公因式法。
(1)(2)(3)(4)多项式多项式多项式多项式的公因式是 b 的公因式是 3 的公因式是 7a 的公因式是 公因式的系数应取各项系数的最大公约数。关键：确定公因式小小测验 感受新知抢答题(找出下列各多项式的公因式):(1)2a+2b(2)xy+yz(3)2ac-4abc(4)m2n+mn2(5)ax+ay-a(6)3m2a-12ma+3ma2(7)(x-y)2+(x-y)(8) –3ax2y+6x3yz点例透视 运用新知 把下列各式分解因式：（1）2x3+6x2（2）3pq3+15p3q（3）4x2-8ax+2x（4）-3ab+6abx-9aby= 2x2(x+3)= 3pq(p2+5q2 )=2x(2x-4a+1)=-3ab(1-2x+3y)通过以上四个例子你觉得提取公因式法分解因式的一般步骤该如何描述？归纳总结 巩固新知 用提取公因式法分解因式的一般步骤是：1、找出：找出应提取的公因式2、除以：用这个多项式去除以公因式， 所得的商作为另一个因式。3、整理：把多项式写成这两个因式的 积的形式。辨一辨下列的分解因式对吗？如果 不对，应怎样改正？（2）（3）（ 漏 项 ）（1） （分解不彻底）（变错符号） 2.一般地，提取公因式后，应使多
项式余下的各项不再含有公因式.
1.注意不要漏项.3.多项式首项系数为负时, 通常应提取负因数，同时剩下的各项都要改变符号.随堂练习随堂练习1将下列各式分解因式（1） （2）议一议下列各式如何分解因式？(1) 3(m+2n)2 + m + 2n(2) 2(a-b)2 – a + b公因式还可以是多项式添括号法则添括号法则：括号前面是“+”号，括到括号里的各项都不变号；括号前面是“-”号，括到括号里的各项都变号。观察分析 归纳总结随堂练习随堂练习2将下列各式分解因式（1） （2） 整理知识 形成网络谈谈本堂课你有哪些收获探究延伸，发展能力1、试一试用简便方法计算（1）（2）（3）（4）如果b-a=－6，ab=7，
那么的值代数式的值为7，求的值。（1）观察多项式，你能看出这个多项式有公因式吗？若将此多项式变形为呢？若有公因式，请写出它的公因式，并将此多项式分解因式。（2）通过对上述多项式的分解因式，你得到什么结论？请用类似的方法分解因式：作业1.A组:1，3，43.选做B: 5(2) ，62.作业本:6.2