5.2单项式的乘法[下学期]

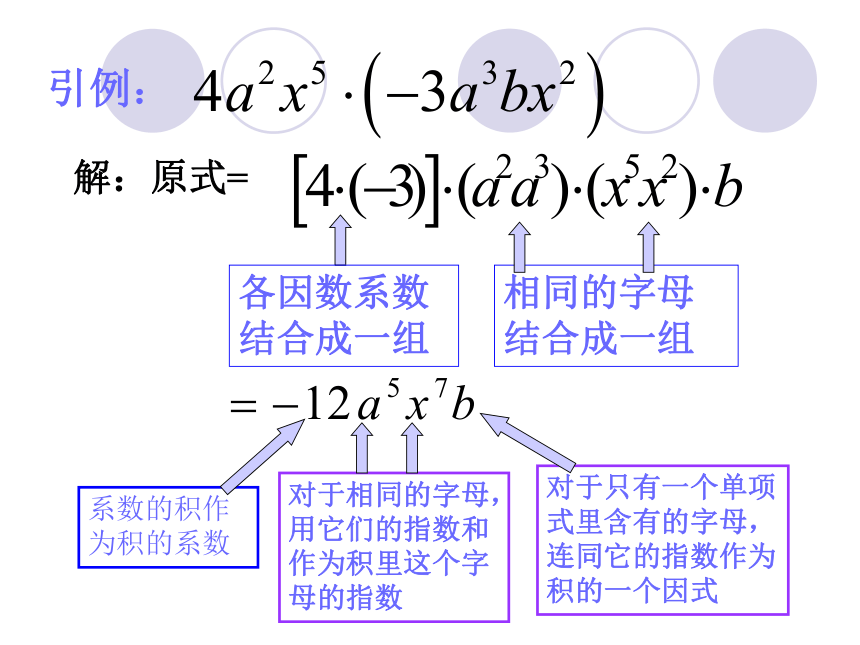
课件28张PPT。 5.2单项式的乘法一位旅行者用步长测量天安门广场的面积：他先从南走到北，记下所走的步数为1100步；再从东走到西，记下所走的步数为625步，然后根据自己的步长来估计广场的面积.问题：（1）如果该旅行者的步长用a米表示，你能用含的a代数式表示广场的面积吗?
（2）假设这位旅行者 的步长为0.8米，那么广场的面积大约是多少平方米？(1100a)·(625a)当a=0.8时(1100a)·(625a)=(1100×0.8)×(625×0.8)=440000m2（3）为了计算简便，我们可以先化简，再代入求值.怎样计算(1100a)·(625a)(1100a)·(625a)=(1100×625)· (a·a)=687500a2问题：运用我们以前学过的哪些运算律和法则？乘法交换律、乘法结合律、同底数幂相乘引例：解：原式=各因数系数结合成一组相同的字母结合成一组系数的积作为积的系数对于相同的字母，用它们的指数和作为积里这个字母的指数对于只有一个单项式里含有的字母，连同它的指数作为积的一个因式单项式与单项式相乘，把它们的系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式。单项式乘法的法则例1 计算：（1）（2）解：（1）原式=（2）原式=例2 计算：（2）原式=(3)原式=解：（1）原式=例3 计算：
（1）（2?104）（5 ? 103） ? 107解（1）原式=（2 ?5)(104 ×103× 107 ）=10?1014=1015(2) (4 ? 105) ·(5 ? 106) ·(3?104)（2）原式=（4?5 ? 3)(105 ? 106 ? 104）=60?1015=6?1016练习1：判断正误：( )( )
( )
( ) ( )
( )×√××××填空-9x3y2a2bXn+2a6nb6n2?1012填空课堂练习-42a5b4c2
-m3n2
-2a4b2c4
6x3y2
-9.85m4n3
单项式乘法中要注意的几点求系数的积，应注意符号；相同字母因式相乘，是同底数幂的乘法，底数不变，指数相加；只在一个单项式里含有的字母，要连同它的指数写在积里，防止遗漏；单项式乘以单项式的结果仍然是一个单项式，结果要把系数写在字母因式的前面；单项式乘法的法则对于三个以上的单项式相乘同样适用。 这次绿色环保活动中购买奖品共花了多少钱？提问：此题有几种算法？各种算法之间有什么联系？ 15(5.20+3.40+0.70)
15×5.20+15×3.40+15×0.70= （1）字母替换数据，在计算方式上有何共性?(2)再将字母换为其它具体数，结论还成立吗？
(3)等式m（a+b+c）=ma+mb+mc
你以前见过吗？
(4)你能知道单项式与多项式相乘的法则吗？
乘法分配律 分配律即单项式与多项式相乘，就是用单项式去乘以多项式的每一项，再把所得的积相加。单项式与多项式相乘法则（1）m（a+b+c）=ma+mb+mc单项式 ×多项式单项式 ×单项式法则的剖析：例5计算：
(1)(－4x)(2x2+3x－1)
(2)(ab2－2ab)ab=(-4x)·2x2+(-4x)·3x+(-4x)·(-1)=-8x3-12x2+4x=ab2 ·ab-2ab·ab=a2b3-2a2b2解（1）原式（2）原式 练习：判断正误（若有错请改正）
① (-6x)(x-3y)=-6x2－18xy

②(3x2－5x+1)(－2x2)
= 6x4+10x3－2x2



①正确判定积的符号；
②积为一个多项式，其项数与多项式的项数相同,不要漏乘了项。
注意例2计算：1、2、3、练一练：1、计算：①②③2、练一练3、1、动脑筋：分别计算下列图形中绿色部分的面积计算： (1) -3a·（2b）=-6ab(2)口答:(1) 1.5x2 · （-2x3）= -3x5(2)(2) (-2a)3 · 2ab2=-8a3 · 2ab2口答: (1) -2(a-b+c)=-2a+2b-2c= -16a4 b2 （1）1cm3干洁 空气中大约有 2.5×1019个分子, 6×103cm3干洁 空气中大约有多少个分子?解: (2.5×1019) (6×103)
=1.5 ×1023 (个)做一做（2）小结1）单项式的乘法法则.2）单项式乘法有理数的乘法同底数幂相乘积的乘方运算转化幂的乘方运算4）单项式与多项式相乘转化单项式与单项式相乘3）单项式与多项式相乘法则.