5.2单项式的乘法[下学期]

课件16张PPT。14.2单项式与多项式相乘1、单项式与单项式相乘的法则？ 2、完成下列各题： ①2x2·(-4xy)=
②(-2x2)·(-3xy)=
③(-9a2 b3)·(8ab2) =
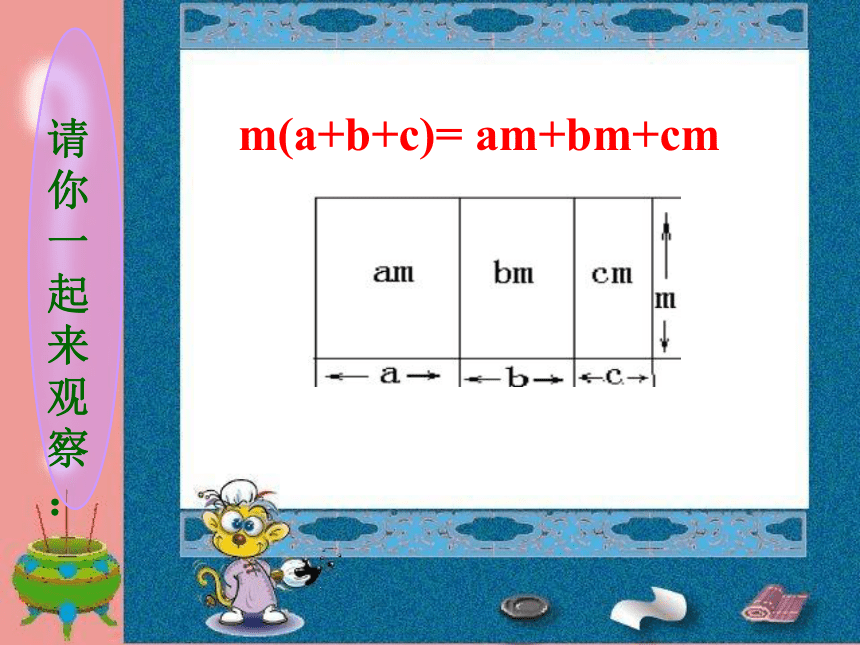
④12×( － + )=-8x3y6x3y-72a3 b59 单项式与单项式相乘，只要将它们的系数、相同字母的幂分别相乘，对于只在一个单项式中出现的字母，则连同它的指数一起作为积的一个因式. 12×( － + )= 你是怎么算的？ 12×( － + ) =12 × － 12 × + 12 ×=8－9 + 10 = 9 m(a+b+c)= am+bm+cm m(a+b+c)= am+bm+cm a·(3a+b)平方米 1).来我们学校的路上看到有一块三角形的路标牌，其一边长(3a+b)米，这条边上的高为2a 米,大家来算一下这块路牌的面积有多少?[列式]2).老师手中的玻璃杯,其底面直径为2a㎝,高为(2b+4) ㎝,请你帮老师算一下这只杯子的体积有多少?[列式]πa2·(2b+4) cm3 例1. 计算： (－2a2) ·(3ab2－5ab3) 法则：单项式与多项式相乘，只要将单项式分别乘以多项式的各项，再将所得的积相加。 a·(3a+b) πa2·(2b+4) =3a2+ ab=2πa2b+4πa2 m(a+b+c)= am+bm+cm = -a3b- 2a2 b2 -5 a3b+ 5a2 b2 解:原式=(-2a2 ) · + (-2a2 ) · b2例2.计算:-2a2( +b2 ) -5a(a2b-ab2) = -6a3b+ 3a2 b2 +(-5a) · a2b+ (-5a) ·(- ab2) 法则：单项式与多项式相乘，只要将单项式分别乘以多项式的各项，再将所得的积相加。 1.计算：
（1）?3x3y ? (2xy2－3xy)；
（2） 2x ?(3x2－xy＋y2);
（3） －3a ?(2a2－a＋4).?2.先化简,再求值。?(x=-2)
x(x2－10)＋3x2(x＋2)－2x(3x－5) ?2.先化简,再求值?(x= -2) x(x2－10)＋3x2(x＋2)－2x(3x－5) 解：原式 ==4x3当x= -2时,原式=4x3=4×(-2)3 =4×(-8) = -32x3–10x+3x3+6 x2–6 x2+10x 1．当多项式中的项数多于三项时，法则是否成立？2 .非零单项式乘以不含同类项的多项式，其积仍是多项式，积的项数与多项式的项数有什么关系？2、解方程：x(x+1)=x2 +33、解不等式：x2+9＞x(x－3)解： x2 + x=x2 +3x=3解：x2+9＞ x2 －3 x3 x ＞ － 9 x ＞ － 3 1、计算：2 an-1(an+1-3a) 解：原式=2an-1· an+1 + 2an-1·(-3a) =2a 2n - 6an 2）已知x+2y=0，
试求x3+2xy(x+y)+4 y3的值1）小斌同学说当n为正整数时， n(4n+1)－4n(n－2)的值是9的倍数，你认为他说的有道理吗？ 提示:原式= x3+2x2 y+2xy2+4 y3 = x2 (x+2y)+2y2 (x+2y)解：2x·4y?小明家新买房子结构如图,父母打算把卧室以外的部分地面铺上地砖，请你帮他们算一下，至少需要购买多少地砖？如果某种地砖价格是a元/㎡，那么购买所需地砖至少要多少元钱？（图中单位为m）至少需要钱：11axy元=11xy+x(4y-2y)+y(4x-3x)1)注意不要漏乘任何一项。 同学们,通过这节课,你觉得单项式与多项式相乘要注意什么呀?2)注意“－”的问题。 3)在几个单项式乘以多项式的混合运算中，要注意运算顺序，完成乘法后，要合并同类项，得出最简结果。 4)逆用单项式与多项式相乘的法则，有时可以简化解题过程。 ?我们的新校园内计划砌一个形状如图甲所示的喷水池，后有人建议改为图乙所示的形状，且外圆直径不变，只是担心原来准备好的材料不够用，请你通过计算，比较一下哪一种方案需要用的材料多（即哪个周长更长）？再 见！2004.11.18Thank you!