单项式的乘法[下学期]

课件12张PPT。5.2单项式的乘法 你知道你的教室有多
大吗?你估算过吗?你知道吗? 计算 : 2abc?3ab2= 单项式与单项式相乘，把它们的系数、同底数幂分别相乘，其余字母连同它的指数不变,作为积的因式. (1) 3b? b2(4) (2×104)(6×103)?107(2) (－6ay3)(－a2) (3) (－3x)3?(5x2y)大胆尝试根据乘法交换律
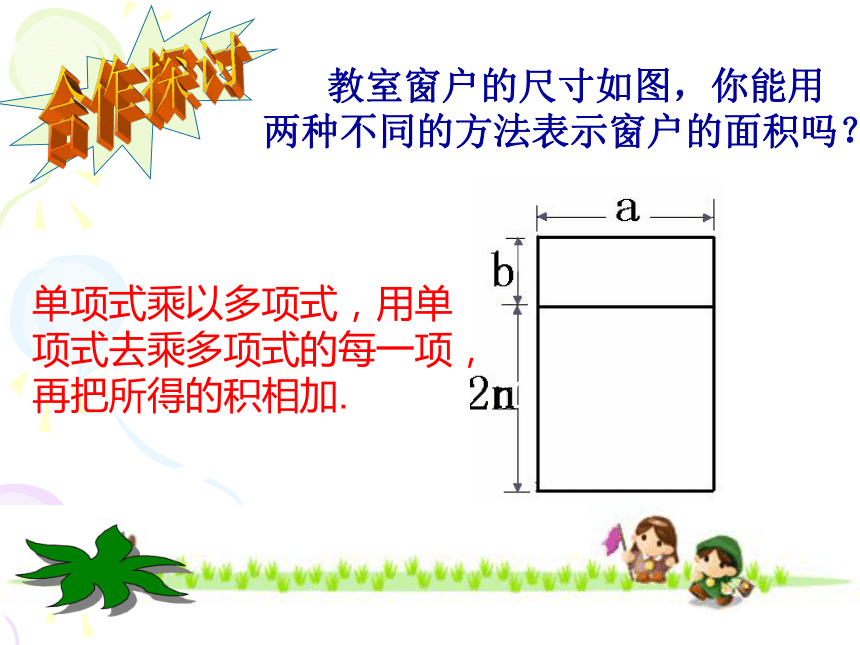
和乘法结合律=6a2b3c根据同底数幂的乘法法则计算:(2×3)(a?a)(b?b2)?c(5) －6a2b(x－y)3?2ab(x－y)2判一判（1） 3a2?2a3 = 6a6（2） 4x25x3 = 9x5（3） (–6a)?(–3a3) = –18a4（4） 3a2b?4a3 = 12a5××××6a520x518a412a5b算一算（1） –3a?(2b)（3） (–2a)3?2ab2（2） 3x?(–5x2y)?(2xyz)合作探讨 教室窗户的尺寸如图，你能用两种不同的方法表示窗户的面积吗？单项式乘以多项式，用单项式去乘多项式的每一项，再把所得的积相加.mn再来算一算（1）2a2b( ab－3ab2)（2）( x－ xy)?(－12y) （3） －3a2(5a－4ab+1)大显身手填一填: (1) ( )?(3x2y2)=81x4y6
(2) 若(my3)?(4yn)2=16y7
则m = , n = .(3) –3a2( –4ab+ )=–15a4+12a3b–3a227x2y4125a21大显身手计算: (1) 2a2(–3ab2) – a(a2b2–2a)(2) a(b–6c)4?a3(b–6c)5回顾与反思单项式乘以单项式单项式乘以多项式转 化有理数运算幂的运算继续尝试bann 下图是某教学楼的平面图你能用几种方法计算平面图的面积？同学们再见!