第五章整式的乘除[下学期]
图片预览

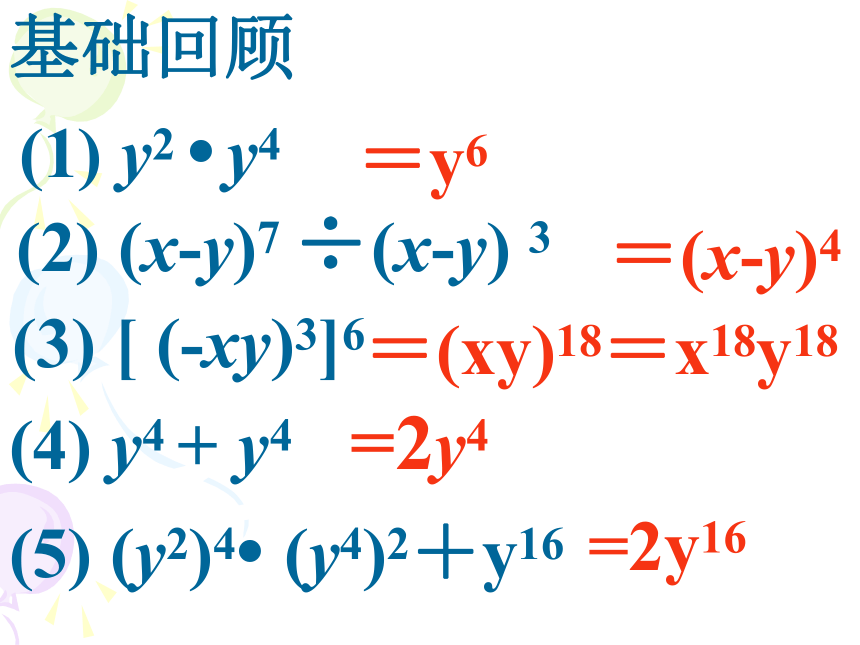




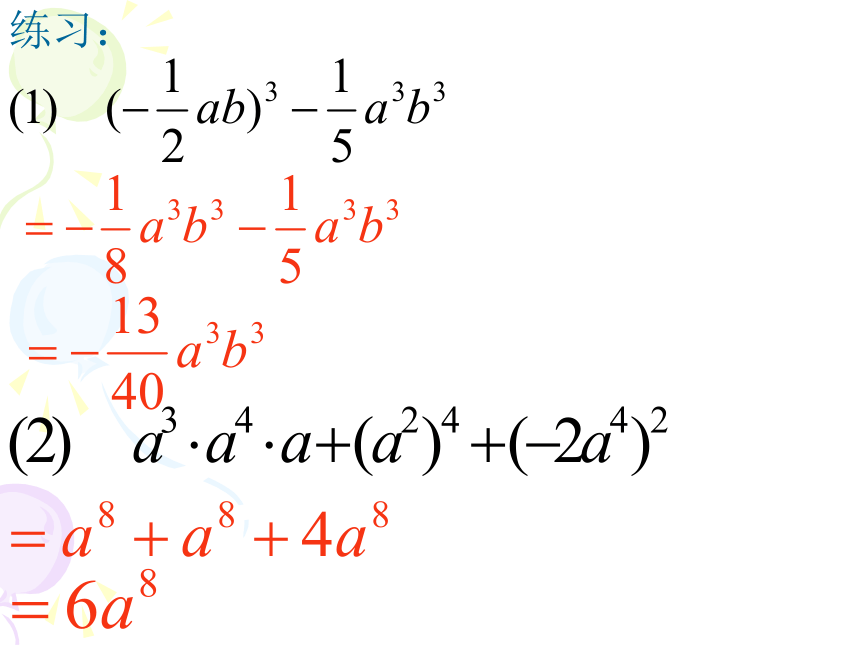
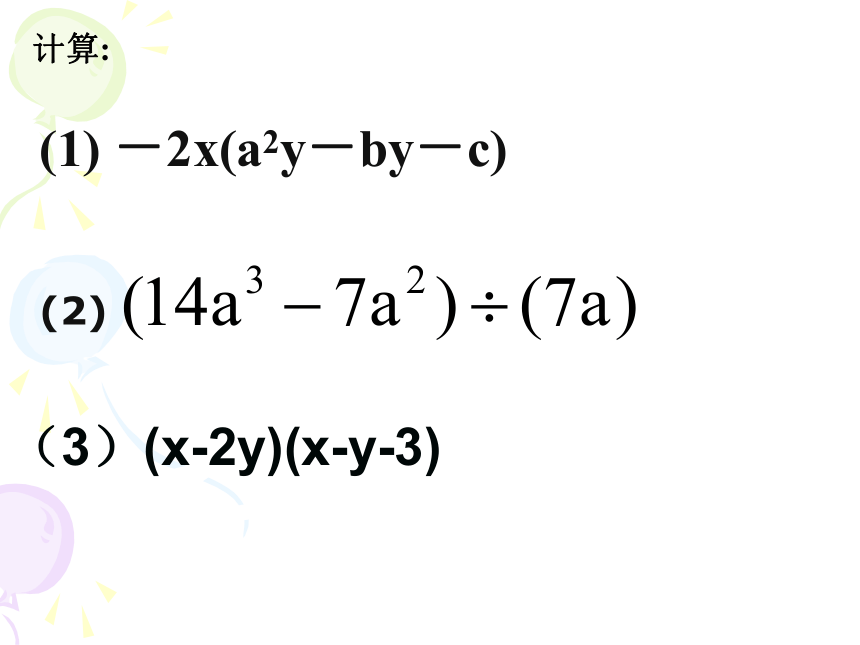




文档简介
课件30张PPT。??整式的乘除复习基础回顾 (3) [ (-xy)3]6 (2) (x-y)7 ÷(x-y) 3 (5) (y2)4? (y4)2+y16(4) y4 + y4(1) y2 ? y4=y6=(x-y)4=(xy)18=x18y18 =2y4=2y16同底数幂的乘法am ?an=am+n (m、n都是正整数) (am)n=amn (m、n都是正整数) 幂的乘方积的乘方(ab)=an bn (n是正整数) 同底数幂的除法am ÷an=am-n (a≠0,m、n都是正整数) (系数×系数)(同底数幂相乘)×单独的幂计算:解:原式=单项式与单项式相乘的法则 (2) (14a4bx)÷(2a2b) = 7a2x单项式乘除 单项式相乘(除),把它们的系数、相同字母分别相乘(除),对于只在一个单项式(除式)里出现的字母,则连同它的指数作为积(商)的一个因式。单项式的除法 单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。练习:计算:(1) -2x(a2y-by-c)(2)(3)(x-2y)(x-y-3)多项式乘以单项式 多项式乘以单项式,用
单项式去乘以多项式的每一
项,并把所得的 积 相加。多项式除以单项式 多项式除以单项式,先
把这个多项式的每一项除以
这个单项式,再把所得的商
相加。a(b+m)+n(b+m)ab+am+nb+nm==(1)(2)(3)1234(a+n)(b+m)多项式乘以多项式 多项式乘以多项式,用一个多项式的每一项去乘以另一个多项式的每一项,并把所得的 积 相加。化简:2(x-8)(x-5)-(2x-1)(x+2)
=2(x2-13x+40)-(2x2+3x-2)= 2x2-26x+80-2x2-3x+2=-29x+82
祝你成功!乘法公式(x+a)(x+b)=x2+(a+b)x+ab(a+b)(a-b)=a2-b2同号2-异号2首平方,尾平方,两倍首尾中间放
公式变形为:(首±尾)2=首2±2×首×尾+尾2(a-b)2=a2-2ab+b2(a+b)2=a2+2ab+b2完全平方公式和的完全平方差的完全平方运用乘法公式计算:(2) (a+b-c)(a-b-c)(3) (x-2y)2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 =x2 - 4xy+4y2a0=1,(a≠0 )用科学记数法表示:-0.0000000461一、判断正误: A.b5?b5=2b5( ) B.x5+x5=x10 ( )
C.(c3)4 ÷c5=c6 ( )
D.(m3?m2)5÷m4=m21 ( ) 二、计算(口答)1.(-3)2?(-3)3=
2. x3?xn-1-xn-2?x4+xn+2=
3.(m-n)2?(n-m)2?(n-m)3=
4. -(- 2a2b4)3=
5.(-2ab)3 ?b5 ÷8a2b4=????-35 xn+2(n-m)3-ab48a6b12(-3)5 =三、 解方程:(2x-3)2 = (x-3)(4x+2)探索与提高3、求证不论x、y取何值,代数式x2+y2+4x-6y+14的值总是正数。即原式的值总是正数证明:x2+y2+4x-6y+14= x2+ 4x + 4+y2-6y+9+1=(x+2)2+(y-3)2+1∵ (x+2)2≥0,(y-3)2 ≥0∴ (x+2)2+(y-3)2+1>04、若10a=20,10b=5-1,求9a÷32b的值。解:∵ 10a ÷ 10b=10a-b∴10a-b=20 ÷ 5-1=100=102∴ a-b=2∵ 9a÷32b= 9a ÷ 9b=9a-b∴ 9a÷32b= 92=81 6. 己知x+y=3 ,x2+y2=5 则xy 的值等于多少?7. 己知x-y=4 , xy=21 ,则 x2+y2 的值等于多少?根据己知条件,确定m ,n 的值
(a)己知:25m·2·10n=57·24 8. 根据己知条件,确定m ,n 的值 (b)己知: (x+1)(x2+mx+n) 的计算结果不含x2和x项。9. 己知:x+x-1=-3 , 求代数式x4+x-4 的值。 9.计算:(a+b)[(a+b)2-3ab](a-b)[(a-b)2+3ab]再见
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。练习:计算:(1) -2x(a2y-by-c)(2)(3)(x-2y)(x-y-3)多项式乘以单项式 多项式乘以单项式,用
单项式去乘以多项式的每一
项,并把所得的 积 相加。多项式除以单项式 多项式除以单项式,先
把这个多项式的每一项除以
这个单项式,再把所得的商
相加。a(b+m)+n(b+m)ab+am+nb+nm==(1)(2)(3)1234(a+n)(b+m)多项式乘以多项式 多项式乘以多项式,用一个多项式的每一项去乘以另一个多项式的每一项,并把所得的 积 相加。化简:2(x-8)(x-5)-(2x-1)(x+2)
=2(x2-13x+40)-(2x2+3x-2)= 2x2-26x+80-2x2-3x+2=-29x+82
祝你成功!乘法公式(x+a)(x+b)=x2+(a+b)x+ab(a+b)(a-b)=a2-b2同号2-异号2首平方,尾平方,两倍首尾中间放
公式变形为:(首±尾)2=首2±2×首×尾+尾2(a-b)2=a2-2ab+b2(a+b)2=a2+2ab+b2完全平方公式和的完全平方差的完全平方运用乘法公式计算:(2) (a+b-c)(a-b-c)(3) (x-2y)2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 =x2 - 4xy+4y2a0=1,(a≠0 )用科学记数法表示:-0.0000000461一、判断正误: A.b5?b5=2b5( ) B.x5+x5=x10 ( )
C.(c3)4 ÷c5=c6 ( )
D.(m3?m2)5÷m4=m21 ( ) 二、计算(口答)1.(-3)2?(-3)3=
2. x3?xn-1-xn-2?x4+xn+2=
3.(m-n)2?(n-m)2?(n-m)3=
4. -(- 2a2b4)3=
5.(-2ab)3 ?b5 ÷8a2b4=????-35 xn+2(n-m)3-ab48a6b12(-3)5 =三、 解方程:(2x-3)2 = (x-3)(4x+2)探索与提高3、求证不论x、y取何值,代数式x2+y2+4x-6y+14的值总是正数。即原式的值总是正数证明:x2+y2+4x-6y+14= x2+ 4x + 4+y2-6y+9+1=(x+2)2+(y-3)2+1∵ (x+2)2≥0,(y-3)2 ≥0∴ (x+2)2+(y-3)2+1>04、若10a=20,10b=5-1,求9a÷32b的值。解:∵ 10a ÷ 10b=10a-b∴10a-b=20 ÷ 5-1=100=102∴ a-b=2∵ 9a÷32b= 9a ÷ 9b=9a-b∴ 9a÷32b= 92=81 6. 己知x+y=3 ,x2+y2=5 则xy 的值等于多少?7. 己知x-y=4 , xy=21 ,则 x2+y2 的值等于多少?根据己知条件,确定m ,n 的值
(a)己知:25m·2·10n=57·24 8. 根据己知条件,确定m ,n 的值 (b)己知: (x+1)(x2+mx+n) 的计算结果不含x2和x项。9. 己知:x+x-1=-3 , 求代数式x4+x-4 的值。 9.计算:(a+b)[(a+b)2-3ab](a-b)[(a-b)2+3ab]再见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
