整式的除法[下学期]

课件14张PPT。标题标题 《数学》5.7整 式整式的除法南浔锦绣实验学校 孔传辉回顾与思考（a ≠ 0）1、用字母表示幂的运算性质：1(5) (a2)3 ·(-a3 )÷(a3)5 ； (6) (x4)6 ÷(x6)2 ·(-x4 )2 。= a10= an= c2=?a9 ÷a15=?a?6=?=x24÷x12 ·x8=x 24 —12+8=x20.类 比 探 索计算下列各题, 并说说你的理由:
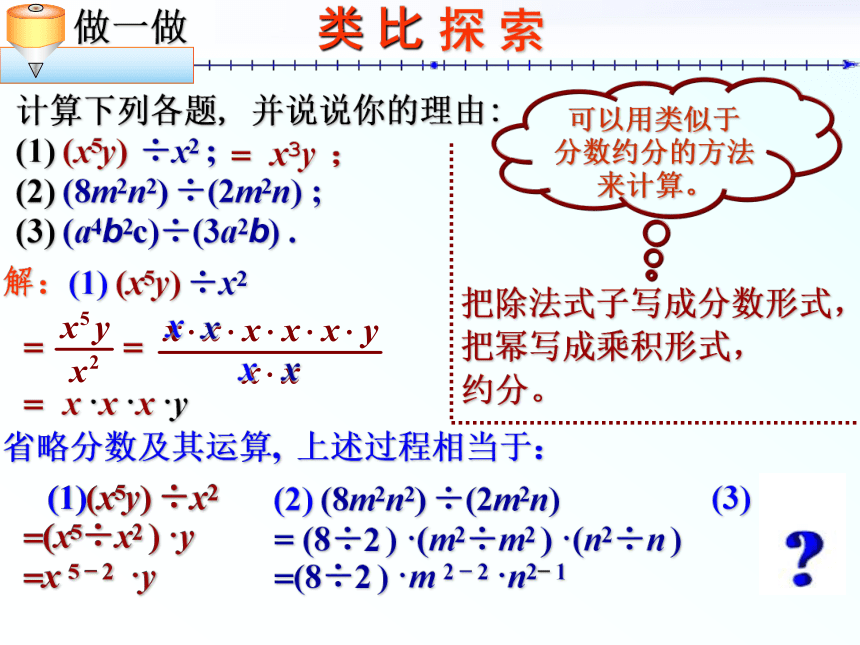
(1) (x5y) ÷x2 ;
(2) (8m2n2) ÷(2m2n) ;
(3) (a4b2c)÷(3a2b) . 解：(1) (x5y) ÷x2 把除法式子写成分数形式，= 把幂写成乘积形式， 约分。== x·x·x·y= x3y ； 省略分数及其运算, 上述过程相当于： (1)(x5y) ÷x2
=(x5÷x2 )·y
=x 5 ? 2 ·y(2) (8m2n2) ÷(2m2n)
==(8÷2 )·m 2 ? 2·n2? 1(3)(8÷2 )·(m2÷m2 )·(n2÷n )探 索 (1)(x5y) ÷x2
=(x5÷x2 )·y
=x 5 ? 2 ·y观察、归纳(1) (x5y) ÷ x2 = x5 ? 2 ·y
(2) (8m2n2) ÷ (2m2n) = (8÷2 )·m2 ? 2·n2 ? 1 ;
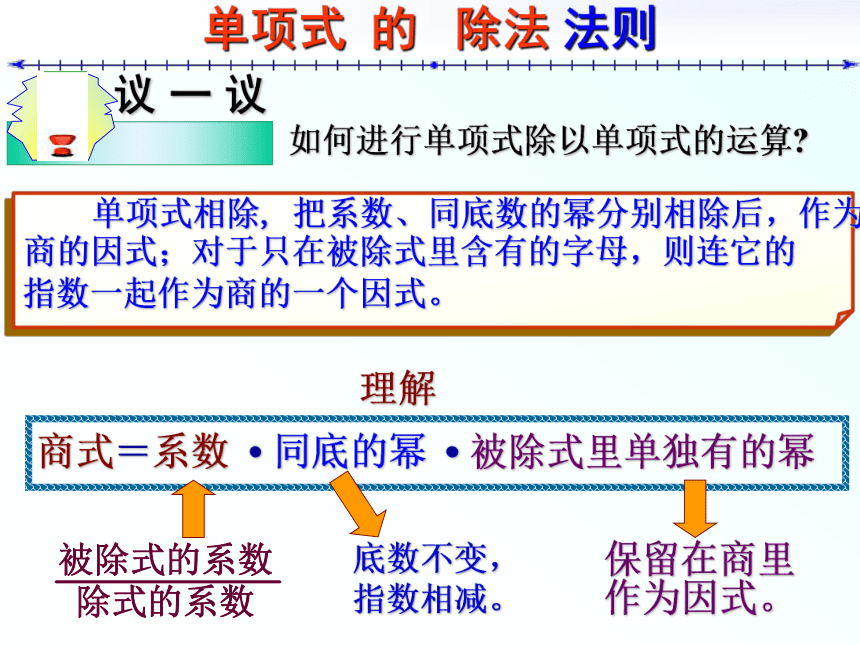
(3) (a4b2c) ÷ (3a2b) = (1÷3 )·a4 ? 2·b2 ?1·c .商式被除式除式 仔细观察一下，并分析与思考下列几点：(被除式的系数)÷ (除式的系数)写在商里面作(被除式的指数) —(除式的指数)商式的系数＝单项式除以单项式，其结果(商式)仍是被除式里单独有的幂，(同底数幂) 商的指数＝一个单项式;？因式。单项式 的 除法 法则如何进行单项式除以单项式的运算? 单项式相除, 把系数、同底数的幂分别相除后，作为
商的因式；对于只在被除式里含有的字母，则连它的
指数一起作为商的一个因式。 底数不变，
指数相减。保留在商里
作为因式。例题解析例题 例1 计算：
(1) ; (2) (10a4b3c2)÷(5a3bc); ?题(3)能这样解吗?
(2x2y)3 ·(?7xy2) ÷ (14x4y3)
=(2x2y)3·[(?7)÷14]·x1?4 y 2?3 (3) (2x2y)3·(?7xy2)÷(14x4y3); (4) (2a+b)4÷(2a+b)2.三块之间是同级运
算, 只能从左到右.?(2a+b)4÷(2a+b)2
=(24a4b4)÷(22a2b2)怎样寻找多项式除以单项式的法则？不妨从最简的多项式除以单项式人手，提示:a+ba+bd dd ddd d( )d怎样寻找多项式除以单项式的法则？( ad+bd )÷d =逆用同分母的
加法、约分：( ad+bd )÷d=(ad)÷d+ (bd)÷d。=上述过程简写为：( ad+bd )÷d=(ad)÷d + (bd)÷d。计算下列各题：
（2）(a2b+3ab)÷a = _________
（3）(xy3–2xy)÷(xy) = _______ab+3by2 –2你找到了 多项式除以单项式的规律 吗？( ad+bd )÷d=(ad)÷d + (bd)÷d。 多项式除以单项式，
先把这个多项式的每一项分别除以单项式，再把所得的商相加。多项式除以单项式的法则例3 计算：（1） 3a+4（2）（3）（4）例题（1） 一共有（ ）项多项式它除以 ，其商式应是（ ）项式， 商式为mm(2)=1(3)( )2答:学 以 致 用 月球距离地球大约 3.84×105千米, 一架飞机的速度约为 8×102 千米/时. 如果乘坐此飞机飞行这么远的距离, 大约需要多少时间 ? 3.84×105 ÷( 8×102 )？这样列式的依据= 0.48×103 ？如何得到的？单位是什么=480(小时) ？如何得到的=20(天) .？做完了吗如果乘坐此飞机飞行这么远的距离, 大约需要20天时间. 你能直接列出一个时间为天的算式吗?3.84×105÷( 8×102 )÷24 .你会计算吗?巩固练 习1、计算填空:⑴ (60x3y5) ÷(?12xy3) = ;综(2) (8x6y4z) ÷( ) =?4x2y2 ;(3) ( )÷(2x3y3 ) = ;合(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;2、能力挑战:?5x2y2?2x4y2z12323x=a,3y=b,则32x-y的值= 。作业 作业教材 p.143课内练习. 以及作业题