第一单元 项目(二)探究计算机中的数据表示——认识数据编码(一)课件 2022—2023学年沪科版(2019)高中信息技术必修1(32张PPT)
文档属性
| 名称 | 第一单元 项目(二)探究计算机中的数据表示——认识数据编码(一)课件 2022—2023学年沪科版(2019)高中信息技术必修1(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
探究计算机中的数据表示
--认识数据编码(一)
授课人:XX
知识回顾
1. 什么是数据?
2. 什么是信息?
3. 数据、信息、知识的关系是什么?
知识
数据
信息
4. 大数据的特征有哪些?
目
录
01
02
03
04
生活中的编码
进制及其转换
数值数据编码
文本数据编码
CONTENTS
01
PART 1
生活中的编码
01
生活中的编码
数牌号
2130198
4080059
编码(encoding)是指用预先规定的方法将文字、数字或其他对象转换成规定的符号组合,给树编号的过程就是一个编码的过程,树牌号是编码的结果。
01
生活中的编码
1. 从下面这个号码你能看出哪些信息?
230103199805082165
黑龙江省哈尔滨市南岗区
2. 你还能说出日常生活中有哪些编码的应用
01
生活中的编码
在计算机中,编码一般是指用预先规定的方法将数字、文字、图像、声音、视 频等对象编成二进制代码的过程。
02
PART 2
进制及其转换
02
进制及其转换
进制是进位计数制
请同学们回顾一下,我们常用的十进制是如何计数的?
十进制的计数规则是逢十进一。
二进制数是怎样的一种形式?进制之间又是如何转换的呢?
进制的基本概念
十进制就是逢十进一
二进制就是逢二进一
十六进制就是逢十六进一
02
进制及其转换
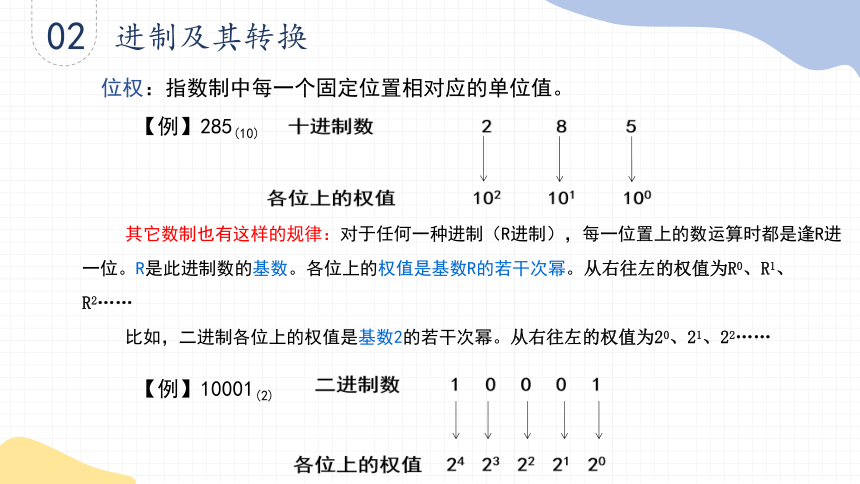
位权:指数制中每一个固定位置相对应的单位值。
【例】285(10)
其它数制也有这样的规律:对于任何一种进制(R进制),每一位置上的数运算时都是逢R进一位。R是此进制数的基数。各位上的权值是基数R的若干次幂。从右往左的权值为R0、R1、R2……
比如,二进制各位上的权值是基数2的若干次幂。从右往左的权值为20、21、22……
【例】10001(2)
02
进制及其转换
数码:一个数制中表示基本数值大小不同的数字符号
十进制的数码:0到9; 二进制的数码:0,1;
基数:指一个数制所使用的数码个数
十进制的基数是10,二进制的基数是2;
位权:指数制中每一个固定位置相对应的单位值。
进位制 二进制 八进制 十进制 十六进制
规则 逢二进一 逢八进一 逢十进一 逢十六进一
基数 R=2 R=8 R=10 R=16
基本符号 (数码) 0,1 0,1,2,…,7 0,1,2,…,9 0,1,..,9,A,..,F
位权 2i 8i 10i 16i
形式表示 (写在数据后面) B O D H
02
进制及其转换
1.二进制只有0和1两个数字符号,基本计数规则是“逢二进一”。
2.计算机外部的各种形式的数据经过编码,都以二进制数的形式存储在计算机里。
二进制
011
101
100
110
111
1000
010
02
进制及其转换
3.二进制位,用比特(bit,简写为b)表示:计算机中存储数据的最小单位。
1比特可以表示0或1两种(21)状态
2比特可以表示00、01、10、11四种(22)状态
8比特构成1字节,可以表示256种(28)状态
02
进制及其转换
4.字节(Byte,简写为B):计算机中存储数据的基本单位。
1字节(Byte)= 8 位(bit)。
数据存储以“字节”(Byte)为单位,数据传输大多以“位”(比特,bit)为单位。
字节
千字节
兆字节
千兆字节
百万兆字节
02
进制及其转换
放进制转换的视频
02
进制及其转换
1.R进制非负整数转换为十进制非负整数
把R(R为不小于2的整数)进制非负整数转换为十进制非负整数,使用“按权展开求和法”。
【例题1】请将11001(2)转换为十进制。
11001(2)=1×24 + 1×23 + 0×22 + 0×21 + 1×20
=16+8+0+0+1=25(10)
【拓展】请将2071(8)转换为十进制。
2071(8)=2×83 + 0×82 + 7×81 + 1×80
=1024+0+56+1 = 1081(10)
02
进制及其转换
2.十进制非负整数转换为R进制非负整数
把十进制非负整数转换为R进制数,可使用短除法,即“除R取余法”。
注:R代表的是不小于2的整数
【例】把18(10)转换为二进制数
答案:10010(2)
18
2
9
2
4
2
2
2
1
2
0
余数
0
1
0
1
0
低位
高位
02
进制及其转换
【例】将175(10)转换为16进制
提示:当R>10时,可能会出现余数为二位数(10)的情况,此时要转换为对应的R进制的单个数字符号。
十进 制数 十六
进制数
1 1
2 2
… …
9 9
10 A
11 B
12 C
13 D
14 E
15 F
02
进制及其转换
【例】将327(8)转换为16进制
提示:当R>10时,可能会出现余数为二位数(10)的情况,此时要转换为对应的R进制的单个数字符号。
十进 制数 十六
进制数
1 1
2 2
… …
9 9
10 A
11 B
12 C
13 D
14 E
15 F
02
进制及其转换
按权展开求和法
短除法(即“除R取余法”)
从低位到高位,每位转成三位二进制
R进制转十进制:
十进制转R进制:
教学目的 3
总结
短除法(即“除R取余法”)
十进制转R进制:
八进制转二进制
十六进制转二进制:
R进制转N进制
先转二进制或十进制,再转成目标进制
八、十六进制相互转换
从低位到高位,每位转成四位二进制
03
PART 3
数值数据编码
03
数值数据编码
原码、反码、补码
原码就是一个数的二进制表达。其中对于有符号数,其最高位为符号位,正数为0,负数为1。
反码和补码是对原码进行某种转换编码方式。
对于正数(或无符号数),原码补码反码三者相同。
对于负数,反码是将原码除了符号位外的每一位数取反,0换为1,1换为0;补码是反码+1。
03
数值数据编码
数值数据的编码以数制表达,计算机中的数值数据以补码的方式表示。可是为什么不用原码或者反码?
计算机是不能直接做减法运算的,因为普通电脑硬件中没有减法器,不需要额外的增加硬件电路制造难度,减法器无需存在。但可以优雅的转换成减法。以计算1-1为例,可以转成1+(-1)
原码:
00000001 + 10000001 = 10000010
10000010 是-2,计算错误。
则:原码不能做计算。
03
数值数据编码
计算【1 - 1 = 0】,若用反码计算:
00000001 + 11111110 = 11111111
此时的8个1是反码,转成原码,就是10000000,也就是 - 0
-0和0也算正确。
但是又会出来一个问题:
0就有两种表示方法:10000000或00000000。这在计算机中被认为是不合理的。则:反码不适合做计算。
计算【1 - 1 = 0】,若用补码计算:
00000001 + 11111111 = 00000000
计算过程中,产生进位,溢出了,所以结果是8个0,为0,计算正确,也解决了反码带来的问题。
则:用补码计算最好。
04
PART 4
文本数据编码
04
文本数据编码
计算机只能处理由0和1这两个二进制数组成的数据
那么文本数据是怎么存储在计算机中的呢?
想一想
04
文本数据编码
文本数据的编码通过对其中每一个字符进行编码实现。
用于文本数据字符编码的方案有多种类型,常见的有ASCII码和Unicode码等。
04
文本数据编码
1.ASCII码
ASCII码,美国信息交换标准码。每一个字符对应一个ASCII码,计算机内部用一个字节(8位)存放一个ASCII码字符,最高位用0表示。例如,“A”的ASCII码为01000001(2),即65(10)。
ASCII码字符集有128个字符。
04
文本数据编码
加密解密游戏
1.首长1
2.发报员
3.收报员
4.首长2
04
文本数据编码
2.中国标准的多个汉字编码方案:
04
文本数据编码
3.Unicode码
世界上有很多套编码,不同编码方案的计算机信息在传递交流的过程中会出现乱码的现象。
Unicode字符集,是全球可以共享的编码字符集,涵盖了世界上主要文字的字符,其中包括简繁体汉字,共计74686个汉字。如汉字“男” 的Unicode编码为30007(10),汉字“女” 的Unicode编码为22899(10)。
感谢观看
授课人:XX
探究计算机中的数据表示
--认识数据编码(一)
授课人:XX
知识回顾
1. 什么是数据?
2. 什么是信息?
3. 数据、信息、知识的关系是什么?
知识
数据
信息
4. 大数据的特征有哪些?
目
录
01
02
03
04
生活中的编码
进制及其转换
数值数据编码
文本数据编码
CONTENTS
01
PART 1
生活中的编码
01
生活中的编码
数牌号
2130198
4080059
编码(encoding)是指用预先规定的方法将文字、数字或其他对象转换成规定的符号组合,给树编号的过程就是一个编码的过程,树牌号是编码的结果。
01
生活中的编码
1. 从下面这个号码你能看出哪些信息?
230103199805082165
黑龙江省哈尔滨市南岗区
2. 你还能说出日常生活中有哪些编码的应用
01
生活中的编码
在计算机中,编码一般是指用预先规定的方法将数字、文字、图像、声音、视 频等对象编成二进制代码的过程。
02
PART 2
进制及其转换
02
进制及其转换
进制是进位计数制
请同学们回顾一下,我们常用的十进制是如何计数的?
十进制的计数规则是逢十进一。
二进制数是怎样的一种形式?进制之间又是如何转换的呢?
进制的基本概念
十进制就是逢十进一
二进制就是逢二进一
十六进制就是逢十六进一
02
进制及其转换
位权:指数制中每一个固定位置相对应的单位值。
【例】285(10)
其它数制也有这样的规律:对于任何一种进制(R进制),每一位置上的数运算时都是逢R进一位。R是此进制数的基数。各位上的权值是基数R的若干次幂。从右往左的权值为R0、R1、R2……
比如,二进制各位上的权值是基数2的若干次幂。从右往左的权值为20、21、22……
【例】10001(2)
02
进制及其转换
数码:一个数制中表示基本数值大小不同的数字符号
十进制的数码:0到9; 二进制的数码:0,1;
基数:指一个数制所使用的数码个数
十进制的基数是10,二进制的基数是2;
位权:指数制中每一个固定位置相对应的单位值。
进位制 二进制 八进制 十进制 十六进制
规则 逢二进一 逢八进一 逢十进一 逢十六进一
基数 R=2 R=8 R=10 R=16
基本符号 (数码) 0,1 0,1,2,…,7 0,1,2,…,9 0,1,..,9,A,..,F
位权 2i 8i 10i 16i
形式表示 (写在数据后面) B O D H
02
进制及其转换
1.二进制只有0和1两个数字符号,基本计数规则是“逢二进一”。
2.计算机外部的各种形式的数据经过编码,都以二进制数的形式存储在计算机里。
二进制
011
101
100
110
111
1000
010
02
进制及其转换
3.二进制位,用比特(bit,简写为b)表示:计算机中存储数据的最小单位。
1比特可以表示0或1两种(21)状态
2比特可以表示00、01、10、11四种(22)状态
8比特构成1字节,可以表示256种(28)状态
02
进制及其转换
4.字节(Byte,简写为B):计算机中存储数据的基本单位。
1字节(Byte)= 8 位(bit)。
数据存储以“字节”(Byte)为单位,数据传输大多以“位”(比特,bit)为单位。
字节
千字节
兆字节
千兆字节
百万兆字节
02
进制及其转换
放进制转换的视频
02
进制及其转换
1.R进制非负整数转换为十进制非负整数
把R(R为不小于2的整数)进制非负整数转换为十进制非负整数,使用“按权展开求和法”。
【例题1】请将11001(2)转换为十进制。
11001(2)=1×24 + 1×23 + 0×22 + 0×21 + 1×20
=16+8+0+0+1=25(10)
【拓展】请将2071(8)转换为十进制。
2071(8)=2×83 + 0×82 + 7×81 + 1×80
=1024+0+56+1 = 1081(10)
02
进制及其转换
2.十进制非负整数转换为R进制非负整数
把十进制非负整数转换为R进制数,可使用短除法,即“除R取余法”。
注:R代表的是不小于2的整数
【例】把18(10)转换为二进制数
答案:10010(2)
18
2
9
2
4
2
2
2
1
2
0
余数
0
1
0
1
0
低位
高位
02
进制及其转换
【例】将175(10)转换为16进制
提示:当R>10时,可能会出现余数为二位数(10)的情况,此时要转换为对应的R进制的单个数字符号。
十进 制数 十六
进制数
1 1
2 2
… …
9 9
10 A
11 B
12 C
13 D
14 E
15 F
02
进制及其转换
【例】将327(8)转换为16进制
提示:当R>10时,可能会出现余数为二位数(10)的情况,此时要转换为对应的R进制的单个数字符号。
十进 制数 十六
进制数
1 1
2 2
… …
9 9
10 A
11 B
12 C
13 D
14 E
15 F
02
进制及其转换
按权展开求和法
短除法(即“除R取余法”)
从低位到高位,每位转成三位二进制
R进制转十进制:
十进制转R进制:
教学目的 3
总结
短除法(即“除R取余法”)
十进制转R进制:
八进制转二进制
十六进制转二进制:
R进制转N进制
先转二进制或十进制,再转成目标进制
八、十六进制相互转换
从低位到高位,每位转成四位二进制
03
PART 3
数值数据编码
03
数值数据编码
原码、反码、补码
原码就是一个数的二进制表达。其中对于有符号数,其最高位为符号位,正数为0,负数为1。
反码和补码是对原码进行某种转换编码方式。
对于正数(或无符号数),原码补码反码三者相同。
对于负数,反码是将原码除了符号位外的每一位数取反,0换为1,1换为0;补码是反码+1。
03
数值数据编码
数值数据的编码以数制表达,计算机中的数值数据以补码的方式表示。可是为什么不用原码或者反码?
计算机是不能直接做减法运算的,因为普通电脑硬件中没有减法器,不需要额外的增加硬件电路制造难度,减法器无需存在。但可以优雅的转换成减法。以计算1-1为例,可以转成1+(-1)
原码:
00000001 + 10000001 = 10000010
10000010 是-2,计算错误。
则:原码不能做计算。
03
数值数据编码
计算【1 - 1 = 0】,若用反码计算:
00000001 + 11111110 = 11111111
此时的8个1是反码,转成原码,就是10000000,也就是 - 0
-0和0也算正确。
但是又会出来一个问题:
0就有两种表示方法:10000000或00000000。这在计算机中被认为是不合理的。则:反码不适合做计算。
计算【1 - 1 = 0】,若用补码计算:
00000001 + 11111111 = 00000000
计算过程中,产生进位,溢出了,所以结果是8个0,为0,计算正确,也解决了反码带来的问题。
则:用补码计算最好。
04
PART 4
文本数据编码
04
文本数据编码
计算机只能处理由0和1这两个二进制数组成的数据
那么文本数据是怎么存储在计算机中的呢?
想一想
04
文本数据编码
文本数据的编码通过对其中每一个字符进行编码实现。
用于文本数据字符编码的方案有多种类型,常见的有ASCII码和Unicode码等。
04
文本数据编码
1.ASCII码
ASCII码,美国信息交换标准码。每一个字符对应一个ASCII码,计算机内部用一个字节(8位)存放一个ASCII码字符,最高位用0表示。例如,“A”的ASCII码为01000001(2),即65(10)。
ASCII码字符集有128个字符。
04
文本数据编码
加密解密游戏
1.首长1
2.发报员
3.收报员
4.首长2
04
文本数据编码
2.中国标准的多个汉字编码方案:
04
文本数据编码
3.Unicode码
世界上有很多套编码,不同编码方案的计算机信息在传递交流的过程中会出现乱码的现象。
Unicode字符集,是全球可以共享的编码字符集,涵盖了世界上主要文字的字符,其中包括简繁体汉字,共计74686个汉字。如汉字“男” 的Unicode编码为30007(10),汉字“女” 的Unicode编码为22899(10)。
感谢观看
授课人:XX
同课章节目录
- 第一单元 数据与信息
- 项目一 探秘鸟类研究——认识数据、信息与知识
- 项目二 探究计算机中的数据表示——认识数据编码
- 单元挑战 认识并制作二维码
- 第二单元 数据处理与应用
- 项目三 调查中学生移动学习现状——经历数据处理的一般过程
- 项目四 认识智能停车场中的数据处理——体验数据处理的方法和工具
- 单元挑战 采集与分析气象数据
- 第三单元 算法和程序设计
- 项目五 描述洗衣机的洗衣流程——了解算法及其基本控制结构
- 项目六 解决温标转换问题——认识程序和程序设计语言
- 项目七 用计算机计算圆周率——设计简单数值数据算法
- 项目八 分析历史气温数据——设计批量数据算法
- 单元挑战 探究密码安全问题
- 第四单元 人工智能初步
- 项目九 了解手写数字识别——体验人工智能
- 单元挑战 尝试人工智能绘画
