第四章 二元一次方程(复习课)[下学期]
文档属性
| 名称 | 第四章 二元一次方程(复习课)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 523.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-31 14:09:00 | ||
图片预览








文档简介
课件22张PPT。有的放矢(课标要求)
(1)方程与方程组(简单的二元一次方程组)
①能够根据具体问题中的数量关系,列出方程,体会方程是刻画现实世界的一个有效的数学模型。
②经历用观察、画图或计算器等手段估计方程解的过程。[参A例7] 2.方程⑤能根据具体问题的实际意义,检验结果是否合理。 第四章 二元一次方程组
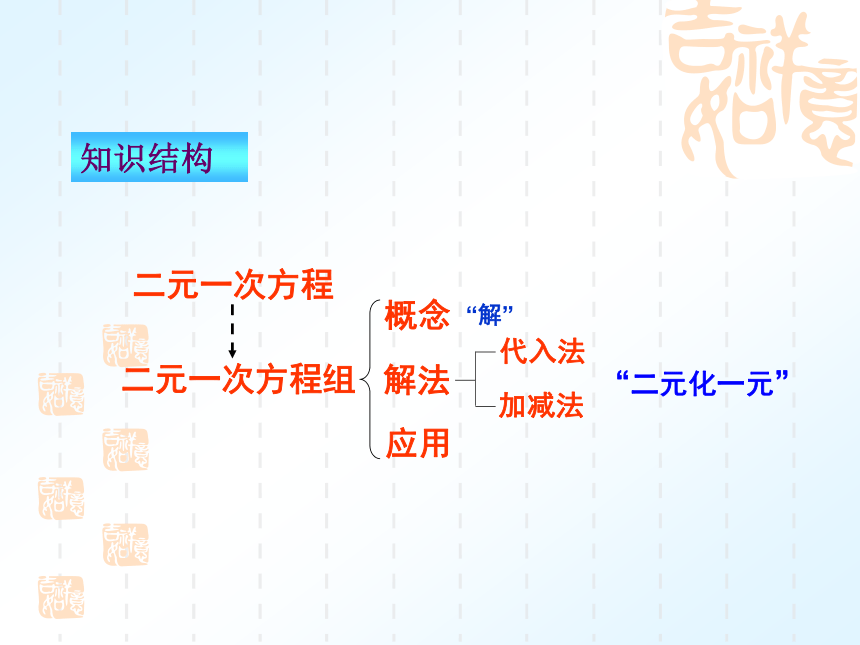
复习课知识结构“解”“二元化一元”(一)二元一次方程组
1.两个含有两个未知数,且未知数的次数是的一次的整式方程组成的一组方程,叫做二元一次方程组.
2.二元一次方程组的一般形式:
3. 二元一次方程组的解法:
(1)加减消元法;
(2)代入消元法.“二元化一元”
1审:分析题意,找出已、未知之间的数量关系和相等关系.
2设:选择恰当的未知数(直接或间接设元),注意单位的同一和语言完整.
3列:根据数量和相等关系,正确列出代数式和方程(组).
4解:解所列的方程(组).
5验: (有三次检验 ①是否是所列方程(组)的解;②是否使代数式有意义;③是否满足实际意义).
6答:注意单位和语言完整.且答案要生活化.(二)、列方程(组)解应用题的一般步骤:三、用代入法解二元一次方程组时,关键要确定先消哪一个未知数。
重要提示:当方程组的两个方程中某一方程的
未知数系数是1的绝对值,
则优先选择此方程中用
含另一个未知数的代数式来表示它,
再代入另一个方程求解。 在求出一个未知数的值后,再求另一个未知数的值,一般选择相对比较简单的一个方程来代,这样会使计算简便。四、当方程组中两个方程的某个未知数的系数相等
或互为相反数时,把方程的两边分别相减或相加来消去这个未知数,得到一个一元一次方程。当方程组中两个未知数系数的绝对值均不相等,可以把两个方程的两边各自乘以一个适当的数,使某一个未知数的绝对值相等。典例解析:1、方程x+2y=7在正整数范围内的解有( )
A 1个 B 2个 C 3个 D 无数个C解后语:二元一次方程一般有无数个解,但它的解若受到限制往往
是有限个解。(2)若x2m-1+5y3n-2m=7是二元一次方程,
则m= ,n= , 11解后语:二元一次方程要求含有未知数项的次数都是1,同时未知数
项的系数不能为零。加y× 2减x
1、 -1=3y 是不是二元一次方程?答: (“是”或“不是”)
2、方程3x – y =1有 个解。
3、方程3x + 2y =1中,当x =1时,y = 。
4、若 是方程3x + y – k =1的一个解,则k = 。
5、已知方程①2x + y =0,②x + 2y =3,那么 能满足的
方程是 (用数字①、②填空)练习:不是无数-12①、②典例解析:当堂练(1)用适当的方法解下列方程组(2)已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值即:m+n=7解:把x=3,y=2代入原方程组,就得到关于a、b的二元一次方程组a=3,b=2 一般地,问题中未知数的个数与相等关系的个数之间的关系怎样?相等.(6)已知x=m+1,y=m-1满足方程3x-y+m=0.由此你可以知道什么?答:知道m.把x=m+1,y=m-1代入方程3x-y+m=0,得3(m+1)-(m-1)+m=0. (7)已知|x+2y+5|+(x-y+1)2=0,求(x+y)2的值.解: 两个非负数的和为0时,这两个有理数只可能都为0,所以由题意,得(x+y)2 =(8)A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?ADBCy°x° B4.(2004重庆)解方程组:中考点击6“鸡兔同笼”是我国古代<<孙子算经>>上的一道名题:你能解决这个有趣的鸡兔同笼问题吗?今有鸡兔同笼,上有35头,下有94足.问鸡兔各几何?.课堂小结1.解二元一次方程组的基本思路:解一元一次方程3.数学解题中,问题中未知数的个数__相等关系的个数等于4.列方程解应用题的步骤:审题;设;列;解;检;答。实际问题分析抽象方程(组)求解检验问题解决列方程解应用题的总思路:祝同学们:学习进步!愿我们:心想事成!再见
(1)方程与方程组(简单的二元一次方程组)
①能够根据具体问题中的数量关系,列出方程,体会方程是刻画现实世界的一个有效的数学模型。
②经历用观察、画图或计算器等手段估计方程解的过程。[参A例7] 2.方程⑤能根据具体问题的实际意义,检验结果是否合理。 第四章 二元一次方程组
复习课知识结构“解”“二元化一元”(一)二元一次方程组
1.两个含有两个未知数,且未知数的次数是的一次的整式方程组成的一组方程,叫做二元一次方程组.
2.二元一次方程组的一般形式:
3. 二元一次方程组的解法:
(1)加减消元法;
(2)代入消元法.“二元化一元”
1审:分析题意,找出已、未知之间的数量关系和相等关系.
2设:选择恰当的未知数(直接或间接设元),注意单位的同一和语言完整.
3列:根据数量和相等关系,正确列出代数式和方程(组).
4解:解所列的方程(组).
5验: (有三次检验 ①是否是所列方程(组)的解;②是否使代数式有意义;③是否满足实际意义).
6答:注意单位和语言完整.且答案要生活化.(二)、列方程(组)解应用题的一般步骤:三、用代入法解二元一次方程组时,关键要确定先消哪一个未知数。
重要提示:当方程组的两个方程中某一方程的
未知数系数是1的绝对值,
则优先选择此方程中用
含另一个未知数的代数式来表示它,
再代入另一个方程求解。 在求出一个未知数的值后,再求另一个未知数的值,一般选择相对比较简单的一个方程来代,这样会使计算简便。四、当方程组中两个方程的某个未知数的系数相等
或互为相反数时,把方程的两边分别相减或相加来消去这个未知数,得到一个一元一次方程。当方程组中两个未知数系数的绝对值均不相等,可以把两个方程的两边各自乘以一个适当的数,使某一个未知数的绝对值相等。典例解析:1、方程x+2y=7在正整数范围内的解有( )
A 1个 B 2个 C 3个 D 无数个C解后语:二元一次方程一般有无数个解,但它的解若受到限制往往
是有限个解。(2)若x2m-1+5y3n-2m=7是二元一次方程,
则m= ,n= , 11解后语:二元一次方程要求含有未知数项的次数都是1,同时未知数
项的系数不能为零。加y× 2减x
1、 -1=3y 是不是二元一次方程?答: (“是”或“不是”)
2、方程3x – y =1有 个解。
3、方程3x + 2y =1中,当x =1时,y = 。
4、若 是方程3x + y – k =1的一个解,则k = 。
5、已知方程①2x + y =0,②x + 2y =3,那么 能满足的
方程是 (用数字①、②填空)练习:不是无数-12①、②典例解析:当堂练(1)用适当的方法解下列方程组(2)已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值即:m+n=7解:把x=3,y=2代入原方程组,就得到关于a、b的二元一次方程组a=3,b=2 一般地,问题中未知数的个数与相等关系的个数之间的关系怎样?相等.(6)已知x=m+1,y=m-1满足方程3x-y+m=0.由此你可以知道什么?答:知道m.把x=m+1,y=m-1代入方程3x-y+m=0,得3(m+1)-(m-1)+m=0. (7)已知|x+2y+5|+(x-y+1)2=0,求(x+y)2的值.解: 两个非负数的和为0时,这两个有理数只可能都为0,所以由题意,得(x+y)2 =(8)A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?ADBCy°x° B4.(2004重庆)解方程组:中考点击6“鸡兔同笼”是我国古代<<孙子算经>>上的一道名题:你能解决这个有趣的鸡兔同笼问题吗?今有鸡兔同笼,上有35头,下有94足.问鸡兔各几何?.课堂小结1.解二元一次方程组的基本思路:解一元一次方程3.数学解题中,问题中未知数的个数__相等关系的个数等于4.列方程解应用题的步骤:审题;设;列;解;检;答。实际问题分析抽象方程(组)求解检验问题解决列方程解应用题的总思路:祝同学们:学习进步!愿我们:心想事成!再见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
