第4章复习[下学期]

课件21张PPT。人们在研究某个自然现象或社会现象时，往往会遇到不方便、不可能或不必要对所有的对象作调查的情况，于是从中抽取一部分对象作调查，这就是抽样。
(4)抽样调查选取的对象应具有代表性
同时抽样调查选取的对象数量应足够活动３想一想 要了解全国初中生的视力情况，有人设计了一种调查方法：
在全国
①按东、西、南、北、中分片，
②每个区域各抽3所中学，
③对这15所中学的全部初中生15000人进行视力测试。
你认为采用哪一种调查方法比较合适？考察对象是什么?在抽样调查中，我们把所要考察的对象的全体叫做总体全国每个学生的视力情况，组成了这个考察的对象把组成总体的每一个考察的对象叫做个体这15000名学生的视力情况又组成一个集体从总体中取出的一部分个体的集体叫做这个总体的一个样本15000样本中的个体的数目叫做样本的容量。1、调查某县农民家庭情况时，从中取出1000名农民进行统计。1.如果要考察的对象内容比较笼统时，样本通常指的是人和物。注意:总体是_　　__________该县的全体农民个体是___________每一个农民总体的一个样本是___________从中取出1000名农民的集体样本容量是___________10002.如果要考察的对象内容是某一方面的特性时，这些特性常常以数据的形式呈现出来。2.为检测一批日光灯的寿命，从中抽样检测50个是日光灯的寿命。总体是_　　　　　__________这批日光灯的寿命的全体个体是__　　　_________每支日光灯的寿命总体的一个样本是　　　　　　　　　　　　　　　　。抽取的各支日光灯的寿命的集体样本容量是___________50（第76页）请指出下列调查哪些应做普查，哪些应作抽样调查：
（1）日光灯管厂要检测一批灯管的使用寿命；
（2）了解居民对废电池的处理情况；
（3）了解现代大学生的主要娱乐方式；
（4）防治某突发性传染病期间，某学校对学生测量体温。
（第77页）某厂家在某城市3个经销该厂产品的大商场进行调查，发现该厂产品的销售量占这3个大商场同类产品销售量的40％，于是该厂声称，他们的产品占国内同类产品销售量的40％。你认为这种宣传可信吗？为什么？平均数的概念:中位数定义：将一组数据按大小依次排列，把处在最中间位置的一个数据（或最中间两个数据的平均数）叫做这组数据的中位数。 众数的定义： 在一组数据中，出现次数最多的数据叫做这组数据的众数。1计算平均数的时候，所有的数据都参加运算，它能成分利用数据所提供的信息，在现实生活中较为常用；但它容易受到极端值的影响。
2中位数的优点计算简单，受极端值的影响较小，但不能充分利用所有数据的信息。
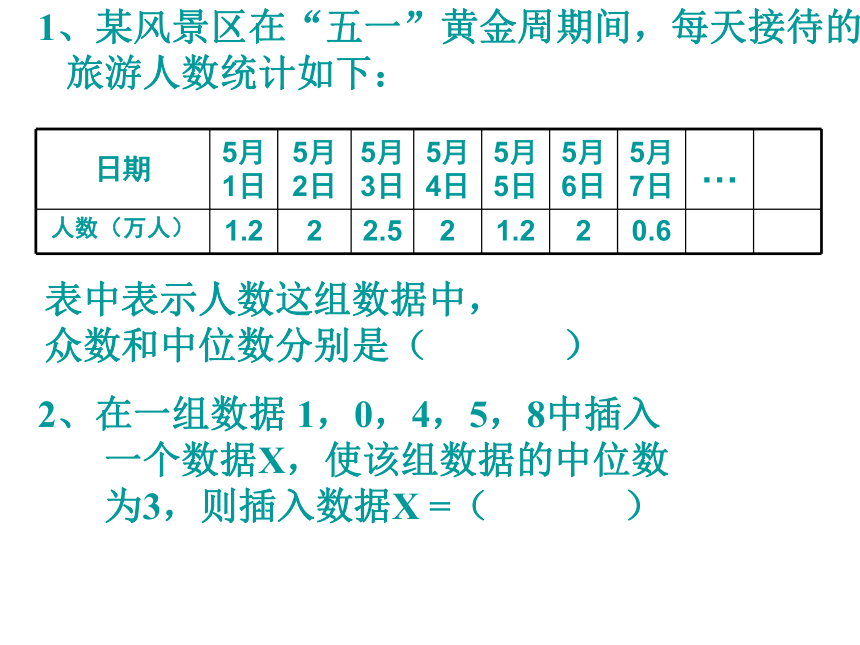
3一组数据中某些数据多次重复出现时，众数往往是人们尤为关心的一个量，但各个数据的重复次数大致相等时，众数往往没有特别意义。1、某风景区在“五一”黄金周期间，每天接待的
旅游人数统计如下：表中表示人数这组数据中，
众数和中位数分别是（ ）2、在一组数据 1，0，4，5，8中插入
一个数据X，使该组数据的中位数
为3，则插入数据X =（ ）平均数、众数及中位数都是描述一组数据的集中趋势的特征数，但描述的角度和适用范围有所不同。
平均数的大小与一组数据里的每个数据均有关系，其中任何数据的变动都会相应引起平均数的变动；
众数着眼于对各数据出现的频数的考察，其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时，其众数往往是我们关心的一种统计量；
中位数则仅与数据的排列位置有关，某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时，可用它来描述其集中趋势。 补充练习1
1、已知一组数据10，10，x,8(由大到小排列)的中位数与平均数相等，求x值及这组数据的中位数。 解：∵10，10，x,8的中位数与平均数相等
∴ (10+x)/2＝ (10+10+x+8)/4 ∴x＝8,
(10+x)/2＝9 ∴这组数据中的中位数是9。2、当5个整数从小到大排列，其中位数是4，如果这个数集的唯一众数是6，则这5个整数可能的最大的和是( )。
A.21 B.22 C.23 D.24。来衡量这组数据的波动大小，并把它叫做这组数据的方差.方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的
波动越大,越不稳定.在学校，小明本学期五次测验的数学成绩和英语成绩分别如下（单位：分）通过对小明的两科成绩进行分析，你有何看法？对小明的学习你有什么建议？我来做1、已知某样本的方差是4，则这个样本的标准差是————。2、已知一个样本1、3、2、x、5，其平均数是3，则这个
样本的标准差是————。探索发现已知三组数据1、2、3、4、5；11、12、13、14、15
和3、6、9、12、15。1、求这三组数据的平均数、方差和标准差。2、对照以上结果，你能从中发现哪些有趣的结论？
想看一看下面的问题吗？32139182反思提高请你用发现的结论来解决以下的问题：
已知数据a1，a2，a3，…，an的平均数为X，方差为Y标准差为Z。则
①数据a1+3，a2 + 3，a3 +3 ，…，an +3的平均数为--------，方差为-------，
标准差为----------。
②数据a1-3，a2 -3，a3 -3 ，…，an -3的平均数为 ----------，方差为--------，
标准差为----------。
③数据3a1，3a2 ，3a3 ，…，3an的平均数为-----------，方差为-----------，
标准差为----------。
④数据2a1-3，2a2 -3，2a3 -3 ，…，2an -3的平均数为 ----------，
方差为---------，标准差为----------。 1.方差:各数据与平均数的差的平方的平均数叫做这 批数据的方差. 2.方差：用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.3.标准差:方差的算术平方根叫做标准差.知识回顾2、中位数：
（1）中位数与数据的排列位置有关，当一组数据中的
个别数据相差较大时，可用中位数来描述这组数
据的集中趋势；
（2）计算方法时：将一组数据按一定的顺序排列起来，
处于最中间位置的一个数（或两个数的平均数）； 3、众数：
众数是对各数据出现频数的考察，其大小只与数据中
部分数据有关，它可能时其中的一个数或多个数； 5、表示数据集中的统计量：平均数、中位数、众数；
表示数据离散的统计量：方差、标准差；
1、某公司销售部有营销人员15人，销售部为了制定某
种商品的月销售额，统计了者15人某月的销售量如下： （1）求者15人营销人员该月销售量的平均数、中位数
和众数；
（2）假设销售部负责人把每位营销人员的月销售量定
为320件，你认为是否合理，为什么？如果不合理，
请你制定一个较合理的销售定额，并说明理由。
平均数为320件,中位数为210件,众数为210件不合理1、公园里有甲、乙两组游客正在做团体游戏，两组
游客的年龄如下：（单位：岁）
甲组：13，13，14，15，15，15，15，16，17，17；
乙组：3，4，4，5，5，6，6，6，54，57；
回答下列问题：
（1）甲组游客的平均年龄是 岁，中位数是 岁，
众数是 岁，其中较好地反映甲组游客年龄特征的是 ；
（2）乙组游客的平均年龄是 岁，中位数是 岁，
众数是 岁，其中较好地反映乙组游客年龄特征的是 ； 151515平均数、众数和中位数155.56中位数和众数