因式分解复习[下学期]

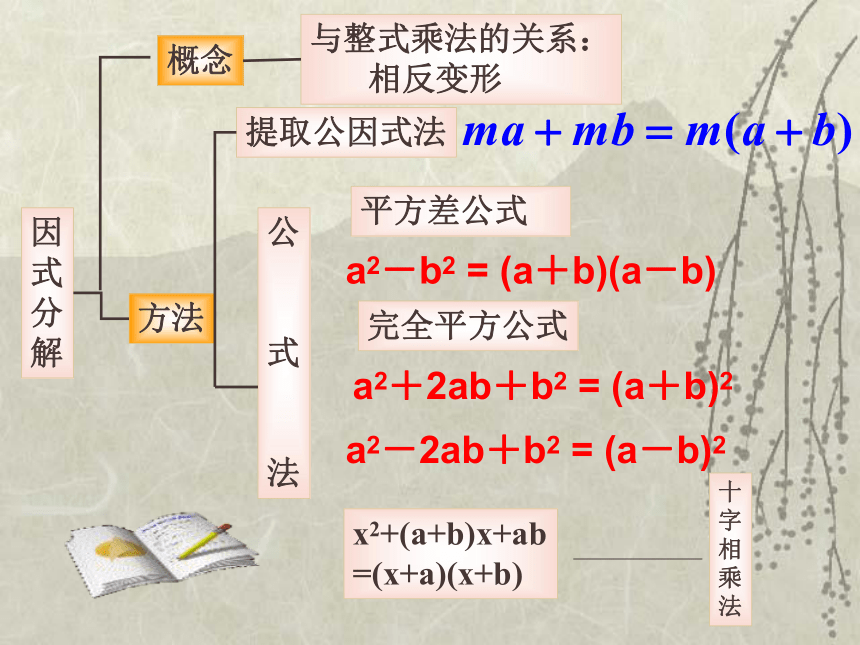
课件20张PPT。感谢各位老师莅临指导因式分解复习课因式分解复习课横店三中 葛政海因
式
分
解概念方法与整式乘法的关系：
相反变形提取公因式法公
式
法平方差公式 完全平方公式x2+(a+b)x+ab
=(x+a)(x+b)十
字
相
乘
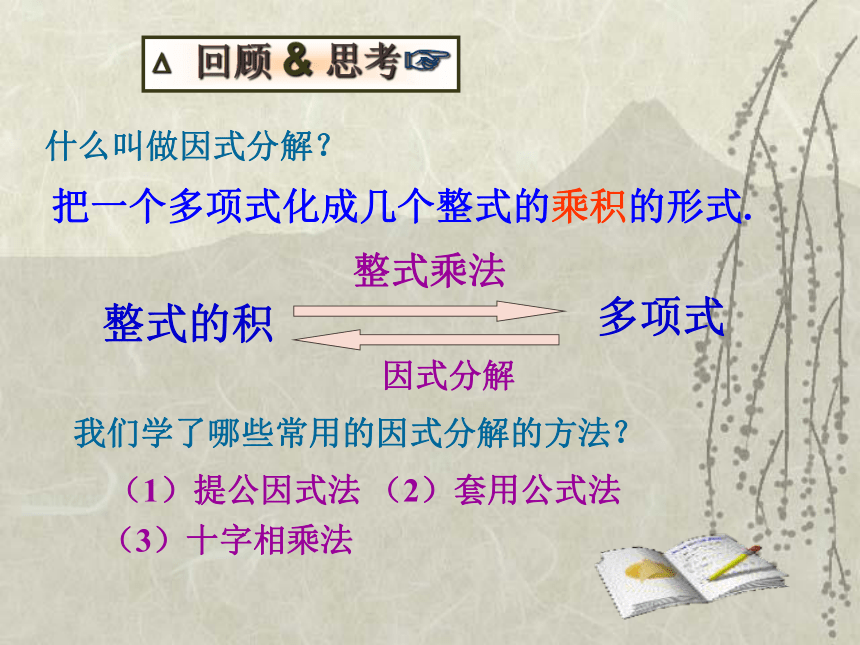
法a2－b2 = (a＋b)(a－b)a2＋2ab＋b2 = (a＋b)2a2－2ab＋b2 = (a－b)2什么叫做因式分解？把一个多项式化成几个整式的乘积的形式.整式的积多项式整式乘法因式分解我们学了哪些常用的因式分解的方法？（1）提公因式法 （2）套用公式法（3）十字相乘法 返回（1）提公因式法提公因式法的关键是确定公因式。 系数取各项系数的最大公约数，字母取相同字母的 最低次幂。公因式:请确定下列多项式中的公因式:(1) 3ay-3by+3y(2) -4a3b2+6a2b-2ab(3) 3(x-y)3-6(x-y)2(4) 5m(a-b)4-4m2(b-a)33y3(x-y)2m(b-a)3-2ab先看有无公因式回顾 & 思考返回（1）提公因式法提公因式法的关键是确定公因式。 系数取各项系数的最大公约数，字母取相同字母的 最低次幂。公因式:把下列多项式因式分解:(1) 3ay-3by+3y(2) -4a3b2+6a2b-2ab(3) 3(x-y)3-6(x-y)2(4) 5m(a-b)4-4m2(b-a)33y(a-b+1)-2ab（2a2b-3a+1) 3(x-y)2(x-y-2)m(b-a)3 (5b-5a-4m)先看有无公因式回顾 & 思考返回（2）套用公式法套用公式法时要注意判断是否符
合公式要求，并熟记公式特征。平方差公式：
完全平方公式：
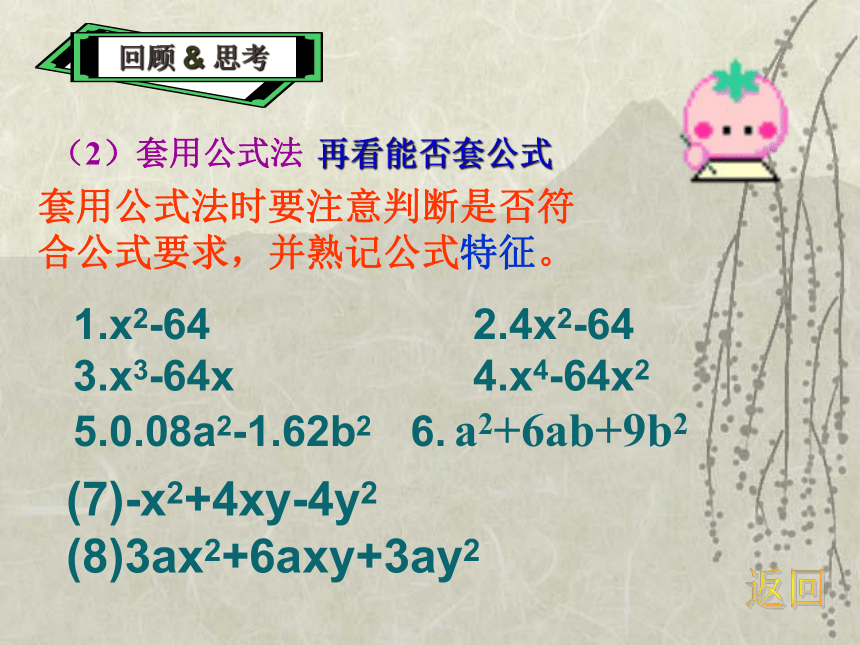
再看能否套公式a2－b2 = (a＋b)(a－b)a2＋2ab＋b2 = (a＋b)2a2－2ab＋b2 = (a－b)2x2+(a+b)x+ab= (x+a)(x+b)回顾 & 思考十字相乘法返回（2）套用公式法套用公式法时要注意判断是否符
合公式要求，并熟记公式特征。再看能否套公式回顾 & 思考1.x2-64 2.4x2-64
3.x3-64x 4.x4-64x2
5.0.08a2-1.62b2 6. a2+6ab+9b2 (7)-x2+4xy-4y2 (8)3ax2+6axy+3ay2返回(9) 25-16x2 (10) -81x2+4(y-1)2
(11) x2-14x+49 (12) (x+y)2-6(x+y)+9
(13) 25(x+y)2-16(x-y)2 (14) x2-6x+8 （2）套用公式法套用公式法时要注意判断是否符合公式要求，并熟记公式特征。再看能否套公式回顾 & 思考计算：（１）（２）（３）运用因式分解进行多项式除法的步骤：1、因式分解2、约去公因式答案：（１）（２）（３）回顾 & 思考4．写出方程的解．解下列方程:用因式分解解方程的一般步骤：1．移项，把方程右边化为零；2．把方程左边因式分解；3．将原方程转化为（一般为两个）一元一次方程；回顾 & 思考例题讲解例1把下列各式分解因式（1） - 2xy - y2 - x2 （2） -1 + p4 （3）x2 - 2xy + y2 + 2x - 2y + 1（4）( a - b)2n - (b - a)2n+1例题讲解例1把下列各式分解因式（1） - 2xy - y2 - x2 =（2） -1 + p4 =（3）x2 - 2xy + y2 + 2x - 2y + 1（4）( a - b)2n - (b - a)2n+1 - (x2 + 2xy + y2)=-(x + y)2 P4 - 1=（p2）2 - 1=(p2 + 1)(p2 - 1)=(p2 + 1)(p + 1)(p - 1)=( x2 - 2xy + y2 ) + ( 2x - 2y) +1=(x - y)2+2(x - y)+1=(x - y + 1)2=(b - a)2n - (b - a)2n+1=(b - a)2n[ 1 - (b - a)]=(b - a)2n( 1 - b+ a)解：巩固练习1（1）若 x2+mx-n能分解成(x-2)(x-5),则
m=???? ,n=??? ??。
（2）x2-8x+m=(x-4)(???? ),且m=?? ??。(3)已知:a+b=7,b-a=3/7 求a2-b2的值(4).若a+b=1,a-2b=3 求a2-ab-2b2的值 (5)若能x2+ax+b分解成(x+3)(x+4),求a,b的值(6).已知代数式x2+3x+5的值是7,求3x2+9x-2的值.巩固练习2（9）把9991分解成两个整数的积。（8）若248－１可以被60与70之间的
两个数整除，求这两个数。7,求证：913 - 324 能被8整除。12,把 a2 - 4ab +3 b2 + 2bc - c2 因式分解。13,已知：| x + y + 1| +| xy - 3 | = 0
求代数式xy3 + x3y 的值。巩固练习3（14）将　　　　再加上一项，使它成为完全平方式，你有几种方法？巩固练习42．解下列方程：1、运用因式分解进行多项式除法：已知　　　 为三角形的三边，试比较　　　　　　与　　 的大小关系．解：为三角形的三边，即挑战自我挑战极限已知：x=2004,求∣4x2 -4x+3 ∣
-4 ∣ x2 +2x+2 ∣ +13x+6的值。解: ∵4x2 - 4x+3= (4x2 - 4x+1)+2 = (2x-1)2 +2 ＞0 x2 +2x+2 = (x2 +2x+1)+1 = (x+1)2 +1＞0∴ ∣4x2 -4x+3 ∣-4 ∣ x2 +2x+2 ∣ +13x+6= 4x2 - 4x+3 -4x2 -8x -8+13x+6= x+1即：原式= x+1=2004+1=2005= 4x2 - 4x+3 -4(x2 +2x+2 ) +13x+6本节课你学到了什么?小结六、拓展和延伸：
1、用简便方法计算：
20052-4010×2003+20032
2、将4x2+1再加上一项，使它成为完全平方式，你有几种方法？
3、分解因式： 4x2+1再见