乘法公式_平方差公式[上学期]

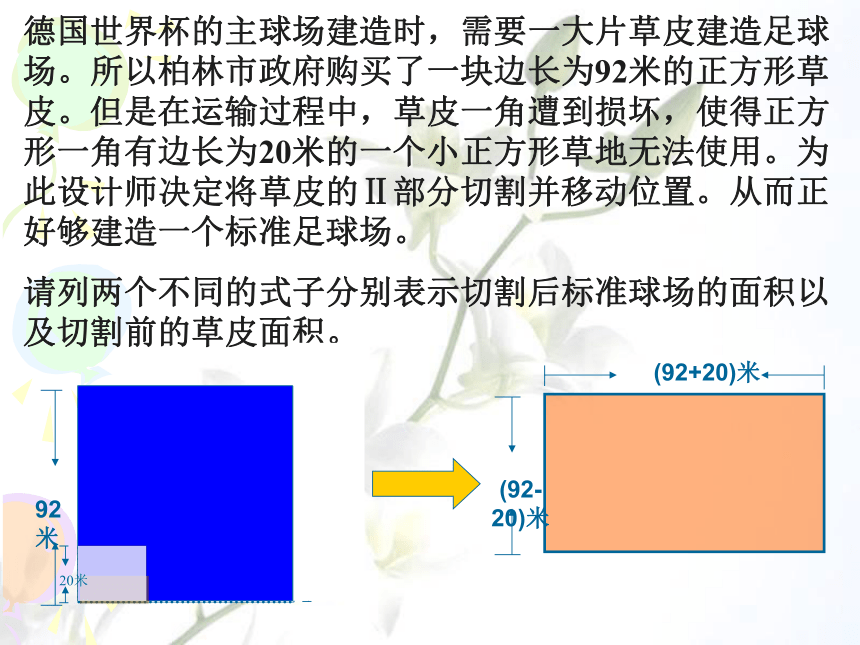
课件25张PPT。5.4乘法公式德国世界杯的主球场建造时，需要一大片草皮建造足球场。所以柏林市政府购买了一块边长为92米的正方形草皮。但是在运输过程中，草皮一角遭到损坏，使得正方形一角有边长为20米的一个小正方形草地无法使用。为此设计师决定将草皮的Ⅱ部分切割并移动位置。从而正好够建造一个标准足球场。
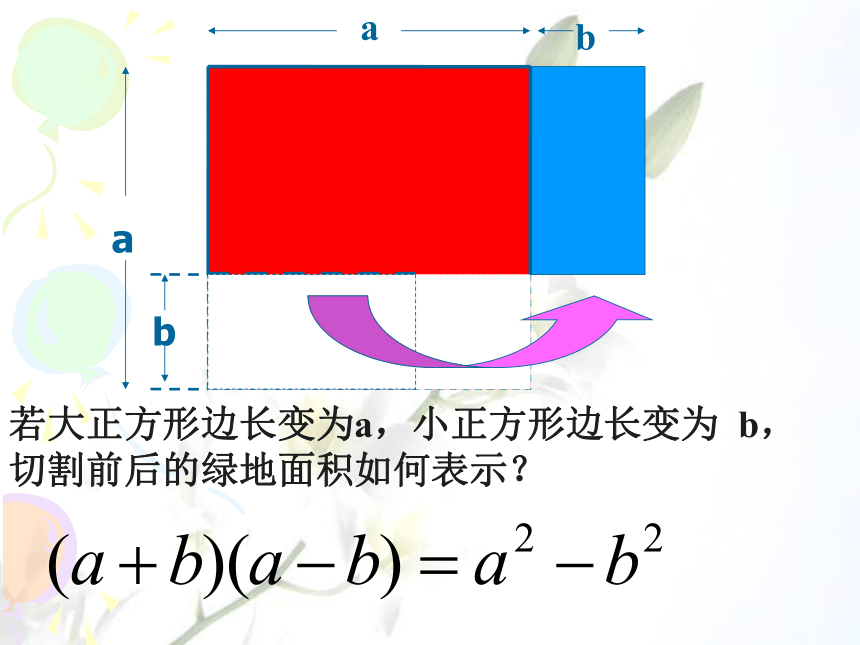
请列两个不同的式子分别表示切割后标准球场的面积以及切割前的草皮面积。 若大正方形边长变为a，小正方形边长变为 b，切割前后的绿地面积如何表示？探究：是否只要(a+b)(a-b)就一定等于？用多项式×多项式来验证。结论：通过图形和数字，我们都证明了这个式子的成立。
推得公式：两个数的和与这两个数差的乘积，等于这两个数的平方差 找出下列各题中的a,b项。（学生寻找，归纳寻找a,b的方法。然后计算。强调给a,b所对应的项定位。）
1. (3m－1 )(3m＋1)
2. (－1+3n)(－1－3n)
3. (－2b－5)(2b－5) 关键：两个二项式中，a前面的符号相同，而b前面的符号相反。所以，找a,b关键是找出符号相同的项和符号相反的项。结果中，符号相同的项放在减号前面，符号相反的项放在减号后面。2019/3/16概念挖掘:判断下列式子是否正确，并说明理由。
判断依据：左边必须是有前面符号相同的项a和前面符号相反的项b。右边必须是左边符号相同的项的平方减去符号相反的项的平方。例题精讲一例1.运用平方差公式进行计算:1.计算（口答）：
（1）（x+1)(x-1)
(2) (x+2)(x-2)
(3) (m+n)(m-n)
(4) (m+6)(m-6)
(5) (x+2y)(x-2y)
(6) (3x-2)(3x+2)
(7) (b+5a)(b-5a) = x2-1= m2-n2= x2-(2y)2 = x2-4y2= m2 - 6 2 = m2-36= (3x)2-22 = 9x2-4= x2 - 4= b2- (5a)2 =b2-25a2判断并改错：
(1) (a+3)(a-3)=a2-3 ( )
改正：
(2)(5y+2)(5y-2)=5y2-4 ( )
改正：
(3) (1- 4xy)(-1- 4xy)=1-16x2y2 ( )
改正：
(4)(-ab+3c)(-3c-ab)=a2b2-9c2 ( )
改正：
(5) (-m+7)(7-m)=m2-49 ( )
改正：××××√(a+3)(a-3)=a2-9(5y+2)(5y-2)=25y2-4原式=(- 4xy+1)(- 4xy-1)=16x2y2-1(-m+7)(7-m)=(7-m)(7-m)=(7-m)2练一练(1)运用平方差公式进行计算:
(1)(x+m)(x-m) (2)(3a+b)(3a-b)
(3)(5a-4b)(5a+4b) (4)(-5x-3y)(-5x+3y)
例题精讲二例2.利用平方差公式计算:
103×97
59.8×60.2 练一练(2)运用平方差公式进行计算:小 结 (a+b)(a-b)=a2- b2两数和与这两数差的积，等于它们的平方差注意1)左边为两个数的和与差的积,右边为两个数的平方差
2)有些式子通过适当变形实质上能用公式
3)公式中的a和b可以是数,也可以是整式
4)最后结果必须化简　已知(N+56)2=1234567,
求(N+46)(N+66)的值运用平方差公式计算:5678×5680-56792=(5679-1)(5679+1)-56792=56792 -1 -56792= -1 利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216如何利用平方差公式计算（1）(a+b+c)(a-b-c)（2）(a-b+c)(a+b-c)（3）(a-b+c)(a-b-c)如果A=1234567892, B=123456788×123456790,
试比较A与B的大小. 若m,n为有理数,式子
的值与n有关吗?试说明理由. 从前有一个狡猾的地主，他把一块长为x米的正方形的土地租给张老汉种植，有一天，他对张老汉说：“ 我把这块地的一边减少5米，另一边增加5米，继续租给你，你也没有吃亏，你看如何？” 张老汉一听觉得没有吃亏，就答应了 ，回到家中，他把这件事对邻居讲了，邻居一听，说：“张老汉你吃亏了！”，张老汉非常吃惊。同学们，你能告诉张老汉这是为什么吗？没有知识就可能上当受骗,不学习就会落后,落后就要挨打,努力吧,同学们!再见