单项式乘法[下学期]
图片预览




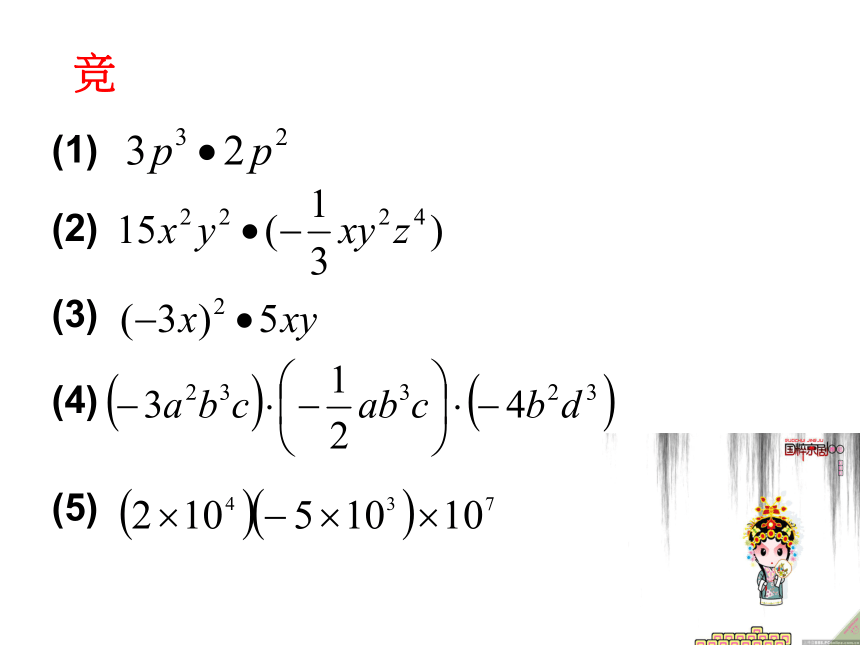


文档简介
课件18张PPT。5.2 单项式的乘法5.2 单项式的乘法浦沿中学知识回顾:3.(am)n=amn (m、n为正整数)
幂的乘方,底数不变,指数相乘.2. am ? an=am+n(m、n为正整数 )
同底数幂相乘,底数不变,指数相加. pam + qam=(p+q) am (m为正整数)
合并同类项法则:系数相加,字母连同指数不变 4. (ab)n=an bn (n为正整数)
积的乘方等于各因数乘方的积。5.由数与字母或字母与字母的乘积组成的代数式叫做单项式.
单独一个数或单独一个字母也是单项式。请你算一算长方形的面积?静5a3a竞
各因式的系数结合成一组相同的字母结合一起一个字母法则:单项式与单项式相乘,把它们的系数、同
底数幂分别相乘,其余字母连同它的指数不变,
作为积的因式.静(1)(5)(4)(2)竞(3)1.求系数的积,应注意符号;2.相同字母因式相乘,运用同底数幂相乘法则;3.防止遗漏只在一个单项式里含有的字母;4.单项式乘法法则适用于三个及三个以上的单项
式相乘.注意:(1) 3x ?4x=12x ( )(2) 7y2 ?8y3=56y6 ( )(3) (- 7m) (- 2m)2= - 28m3 ( )(4) (- 2a2b3)2 (- 3a3b2)=12a7b8 ( )判断下列计算是否正确,并简要说明理由××
√×竞
竞mm5a3a如果贴两条宽为m的纸条,此时面积是多少?你能用两种方法思考吗?利用乘法分配律如何计算:法则:单项式与多项式相乘,用单项式去乘多项
式的每一项,再把所得的积相加.静(1)(4)(3)(2)竞1.运用单项式与多项式相乘法则时,要注意到单项式 与多项式的每一项相乘,不能漏乘.2.单项式乘以多项式的结果是一个多项式,积的项数与因式中的多项式项数相同.3.运用法则时,要注意运算过程中的符号对积的影响,当单项式带正号,乘积的每一项符号与原多项式的符号相同:当单项式带负号,乘积的每一项符号与原多项式的符号相反:说明:(1) -m(a-b)=-ma-mb ( )(2) (a-3b)?(-6a)=-6a2-18ab ( )(3) (-x2y)(-9xy+1)=9x3y2+1( )(4) (2ab2-3ab)(-3ab)=-6a2b3+9a2b2 ( ) 判断下列计算是否正确,并简要说明理由.竞×××√竞竞谁厉害:
(3)(1)(2)(4)填一填:(1)已知:
则m= a= b= (2) 已知
(m是小于10的自然数),则m= , n=___:挑战自我挑战自我已知,求的值。 如果x3ym-1 ?xn+m ?y2n+2 与-3x9y9是同类项,求4m-3n的值
若(2xnyn+m)3=8x9y15成立,则求m与n的值.
聪明题(1)(2)算一算: (1)(4)(3)(2)
幂的乘方,底数不变,指数相乘.2. am ? an=am+n(m、n为正整数 )
同底数幂相乘,底数不变,指数相加. pam + qam=(p+q) am (m为正整数)
合并同类项法则:系数相加,字母连同指数不变 4. (ab)n=an bn (n为正整数)
积的乘方等于各因数乘方的积。5.由数与字母或字母与字母的乘积组成的代数式叫做单项式.
单独一个数或单独一个字母也是单项式。请你算一算长方形的面积?静5a3a竞
各因式的系数结合成一组相同的字母结合一起一个字母法则:单项式与单项式相乘,把它们的系数、同
底数幂分别相乘,其余字母连同它的指数不变,
作为积的因式.静(1)(5)(4)(2)竞(3)1.求系数的积,应注意符号;2.相同字母因式相乘,运用同底数幂相乘法则;3.防止遗漏只在一个单项式里含有的字母;4.单项式乘法法则适用于三个及三个以上的单项
式相乘.注意:(1) 3x ?4x=12x ( )(2) 7y2 ?8y3=56y6 ( )(3) (- 7m) (- 2m)2= - 28m3 ( )(4) (- 2a2b3)2 (- 3a3b2)=12a7b8 ( )判断下列计算是否正确,并简要说明理由××
√×竞
竞mm5a3a如果贴两条宽为m的纸条,此时面积是多少?你能用两种方法思考吗?利用乘法分配律如何计算:法则:单项式与多项式相乘,用单项式去乘多项
式的每一项,再把所得的积相加.静(1)(4)(3)(2)竞1.运用单项式与多项式相乘法则时,要注意到单项式 与多项式的每一项相乘,不能漏乘.2.单项式乘以多项式的结果是一个多项式,积的项数与因式中的多项式项数相同.3.运用法则时,要注意运算过程中的符号对积的影响,当单项式带正号,乘积的每一项符号与原多项式的符号相同:当单项式带负号,乘积的每一项符号与原多项式的符号相反:说明:(1) -m(a-b)=-ma-mb ( )(2) (a-3b)?(-6a)=-6a2-18ab ( )(3) (-x2y)(-9xy+1)=9x3y2+1( )(4) (2ab2-3ab)(-3ab)=-6a2b3+9a2b2 ( ) 判断下列计算是否正确,并简要说明理由.竞×××√竞竞谁厉害:
(3)(1)(2)(4)填一填:(1)已知:
则m= a= b= (2) 已知
(m是小于10的自然数),则m= , n=___:挑战自我挑战自我已知,求的值。 如果x3ym-1 ?xn+m ?y2n+2 与-3x9y9是同类项,求4m-3n的值
若(2xnyn+m)3=8x9y15成立,则求m与n的值.
聪明题(1)(2)算一算: (1)(4)(3)(2)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
