乘法公式(-)[下学期]

课件16张PPT。5.4乘法公式(-)
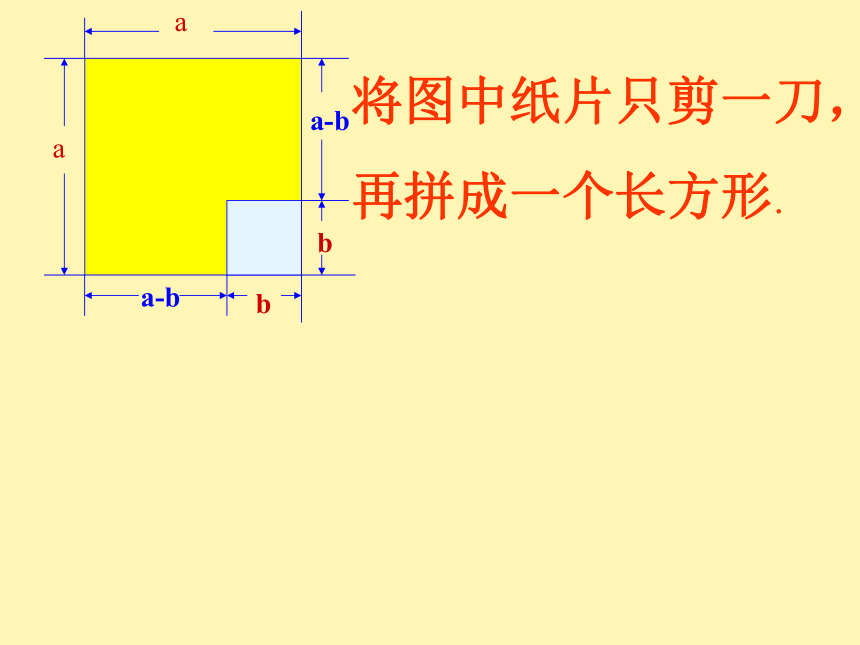
平方差公式用自己的语言叙述你的发现。观察以上算式及其运算结果，你发现了什么规律？用式子表示将图中纸片只剪一刀，
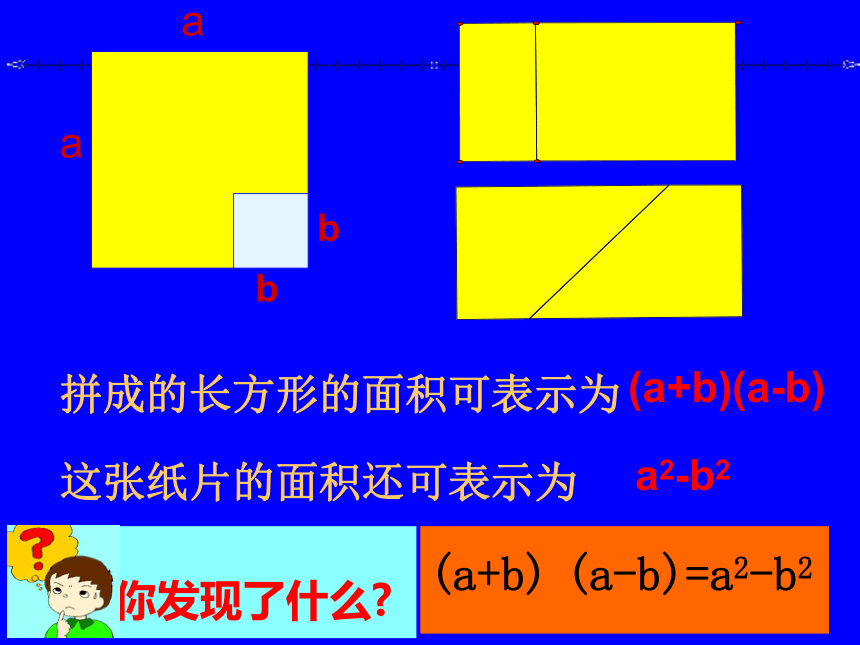
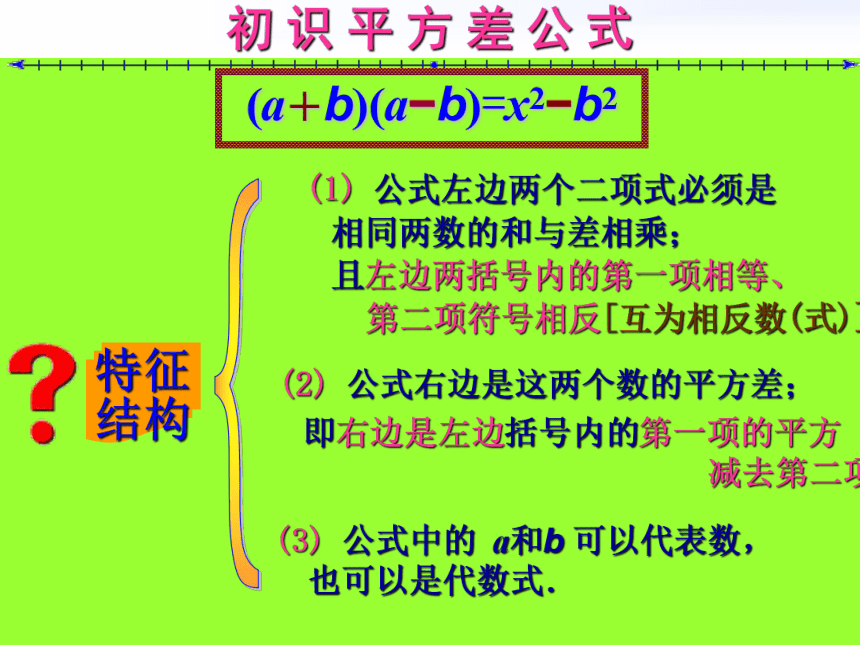
再拼成一个长方形．a-bbba-baaaabba-ba-b拼成的长方形的面积可表示为＿＿＿＿＿.这张纸片的面积还可表示为___________.(a+b)(a-b)a2-b2你发现了什么?(a+b) (a-b)=a2-b2初 识 平 方 差 公 式(a+b)(a?b)=x2?b2 (1) 公式左边两个二项式必须是相同两数的和与差相乘； 且左边两括号内的第一项相等、 第二项符号相反[互为相反数(式)];(2) 公式右边是这两个数的平方差； 即右边是左边括号内的第一项的平方
减去第二项的平方. (3) 公式中的 a和b 可以代表数，
也可以是代数式． 纠 错 练 习(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2本题对公式的直接运用，以加深对公式本质特征的理解． 指出下列计算中的错误： 第二数被平方时，未添括号。第一 数被平方时，未添括号。第一数与第二数被平方时，
都未添括号。拓 展 练 习(1) (a+b)(?a?b) ；
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 本题是公式的变式训练，以加深对公式本质特征的理解． 下列式子可用平方差公式计算吗? 为什么? 如果能够，怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 练习