同底数幂的乘法(一)[下学期]
图片预览


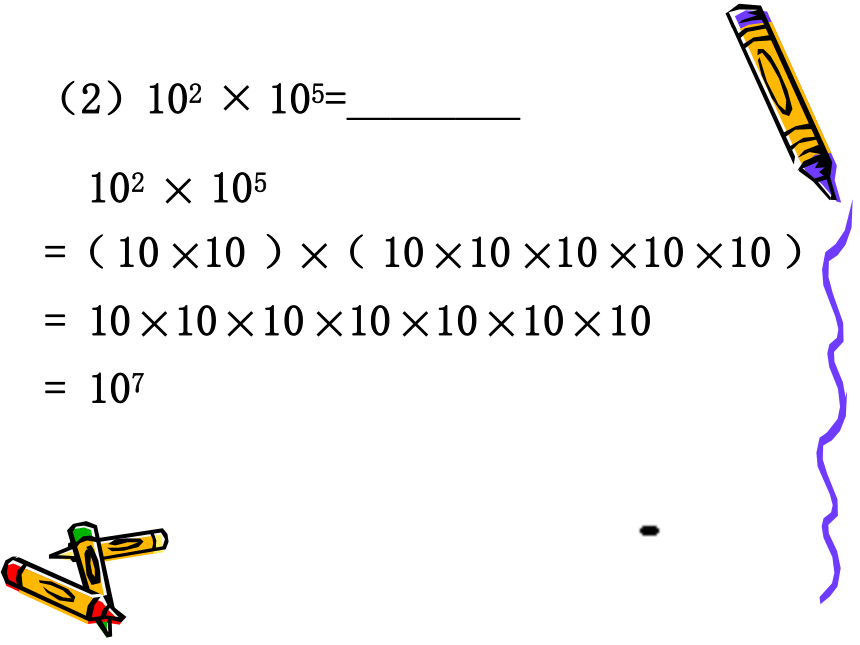
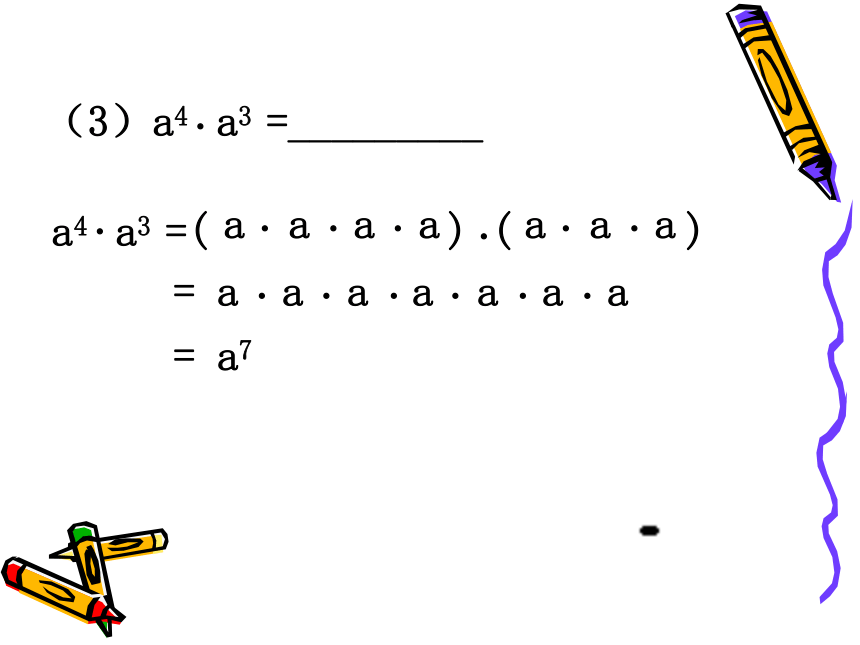


文档简介
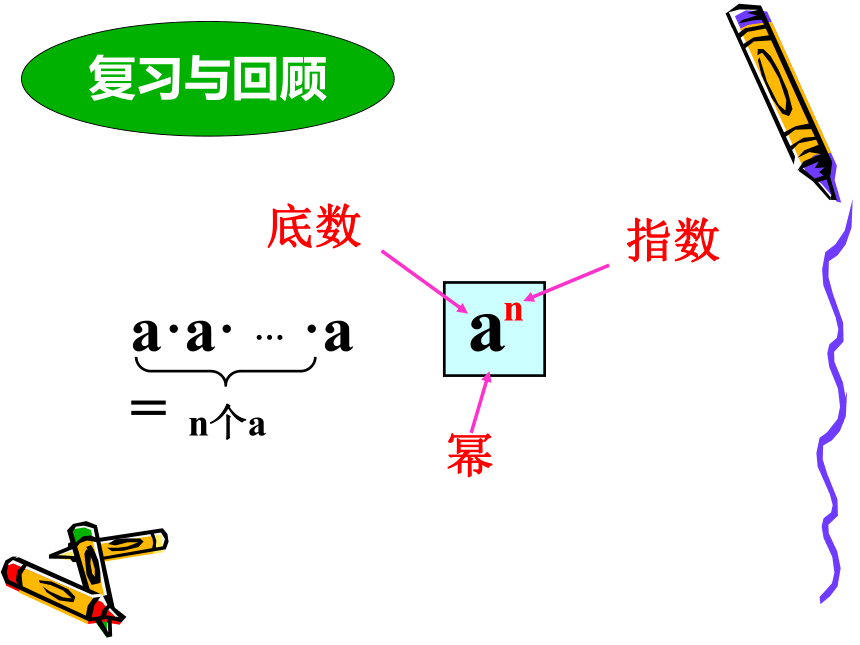
课件15张PPT。5.1 同底数幂的乘法复习与回顾指数幂底数做一做(1)23 22 = _________你还能用其他方法计算吗?23 22 是多少个2相乘?23 22 =(2 2 2)(2 2)= 2 2 2 2 2= 25(2)102 105=________102 105=( ) ( ) 10 1010 10 10 10 10= 10 10 10 10 10 10 10= 107(3)a4 a3 =_________..= a723 22 =25102 105= 107a4 a3 =.a7你发现同底数幂相乘有什么规律?= 23+2= 102+5= a4+3同底数幂的乘法法则: 同底数幂相乘,底数______,
指数_______。不变相加 计算下列各式,结果用幂的形式表示:(1)(2)(3)(4)例1: 运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果:(1)(2)(3)(4)练习:辨一辨:(1) x · x4= x4 ( )
(2) 32×3m = 32m ( )
(3) (-3)5 · (-3)3= 38 ( )
b3+b3 = b6 ( )x53m+22b3√××× a2·a3- a3·a2 = 0 ( )
(6) x3·y5=(xy)8 ( )
(7) x2·x2=2x4 ( )√×x3y5×x4下面计算是否正确?若不正确请加以纠正。 am · an · ap 等于什么?(1)(2)(-7)8 · 73 等于什么?想一想:(-7)3 · 78呢? 运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果:(1)(2)(3)(4)(5)(6)(7)练习: 我国自行研制的“神威1”计算机的峰值运算速度达到每秒3840亿次。如果按这个速度工作一整天,那么它能运算多少次?(结果保留3个有效数字)例2:1、如果 , 则 n=_______2、已知10m=4,10n=11,求10m+n =______思考:同底数幂的乘法性质:底数 ,指数 .不变相加幂的意义:小 结
指数_______。不变相加 计算下列各式,结果用幂的形式表示:(1)(2)(3)(4)例1: 运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果:(1)(2)(3)(4)练习:辨一辨:(1) x · x4= x4 ( )
(2) 32×3m = 32m ( )
(3) (-3)5 · (-3)3= 38 ( )
b3+b3 = b6 ( )x53m+22b3√××× a2·a3- a3·a2 = 0 ( )
(6) x3·y5=(xy)8 ( )
(7) x2·x2=2x4 ( )√×x3y5×x4下面计算是否正确?若不正确请加以纠正。 am · an · ap 等于什么?(1)(2)(-7)8 · 73 等于什么?想一想:(-7)3 · 78呢? 运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果:(1)(2)(3)(4)(5)(6)(7)练习: 我国自行研制的“神威1”计算机的峰值运算速度达到每秒3840亿次。如果按这个速度工作一整天,那么它能运算多少次?(结果保留3个有效数字)例2:1、如果 , 则 n=_______2、已知10m=4,10n=11,求10m+n =______思考:同底数幂的乘法性质:底数 ,指数 .不变相加幂的意义:小 结
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
