同底数幂的乘法[下学期]

课件22张PPT。准备好了吗?生活中的问题,幻灯片 4 5.1同底数幂的乘法生活中问题地球距离太阳大约有多远?光的速度约为太阳光照射到地球上大约需
猜想论证,幻灯片 63幻灯片 4 返回生活中的问题猜想:同底数幂相乘,什么不变?
什么变了,怎么变的?即论证猜想,幻灯片 7一个例子不能说明问题，我们不妨多举几个例子。数学讲究事实胜于雄辩，你们能否证明你们猜想?=(10 ×10 ×10) ×(10 ×10 ) ( )=10 ×10 ×10 ×10 ×10 ( )103×102根据幂的意义根据乘法结合律=105 ( )根据幂的意义 即：103 × 102 = 105 猜想:当底数是字母时,
是否也有同底数幂相乘,底数不变,指数相加.论证猜想,幻灯片 8 结论:当底数是字母时,
也有同底数幂相乘,底数不变,指数相加.进一步猜想:当底数和指数都是字母时,是否也有同底数幂相乘,底数不变,指数相加.猜想论证,幻灯片 9结论:当底数和指数都是字母时,
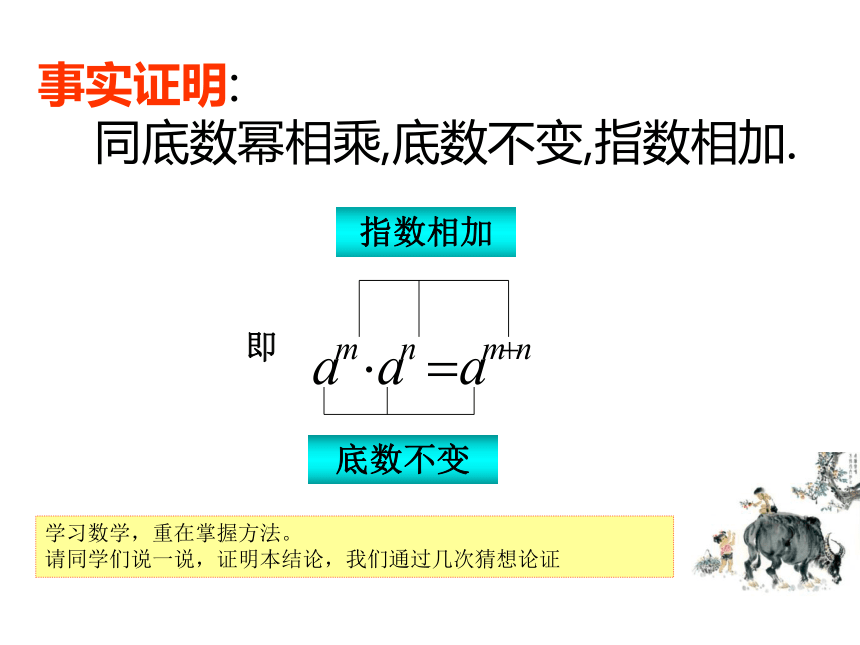
也有同底数幂相乘,底数不变,指数相加. 论证总结 幻灯片 10事实证明:
同底数幂相乘,底数不变,指数相加.学习数学，重在掌握方法。
请同学们说一说，证明本结论，我们通过几次猜想论证猜想1:当底数和指数都是数字时,
是否有同底数幂相乘,底数不变,指数相加.猜想2:当底数是字母时,
是否也有同底数幂相乘,底数不变,指数相加.猜想3:当底数和指数都是字母时,
是否也有同底数幂相乘,底数不变,指数相加.分类讨论思想am · an = am+n (当m、n都是正整数)同底数幂相乘,想一想： 当三个或三个以上同底数幂相乘时，是否也 　? 具有这一性质呢？ 怎样用公式表示？底数　　，指数　　。不变相加 同底数幂的乘法法则：　请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.如 43×45=43+5=48 如 am·an·ap = am+n+p （m、n、p都是正整数） 注意:条件：①乘法 ②同底数幂　
结果：①底数不变 ②指数相加 计算下列各式，结果用幂的形式表示：⑴、78 ×73⑶、x3 x5(4)、(a-b)2 (a-b) 合作交流　请同桌之间互出两道同底数
幂相乘题，让对方做，看谁做
得最好！！！？请帮忙出出主意：
当底数出现互为相反数时，该怎么办呢？ 计算下列各式，结果用幂的形式表示负的偶次幂为正，负数的奇次幂为负；
先确定符号，再把指数相加下面的计算对不对？如果不对，应怎样改正？⑴、⑶、⑸、⑷、⑵、底数不变，指数相加合并同类项，系数相加。 要发挥每个指数的作用负数的偶次幂为正负数的奇次幂为负注意法则使用的条件；
同底数幂相乘时，指数是相加的；
不能疏忽指数为1的情况；
运算结果的底数一般应为正数．
若底数不同，先化为相同，后运用法则． 冷静反思通过上面的练习你认为同底数幂
的乘法法则的应用应注意什么? 例2 我国自行研制的“神威Ⅰ”计算机的峰值运算速度达到每秒3840亿次。如果按这个速度工作一整天，那么它能运算多少次？ （结果保留3个有效数字）解：3840亿次=3.84×103×108次24时=24×3.6×103秒（3.84×103×108 ）×（24×3.6×103）=（3.84×24×3.6）×（103×108×103）= 331.776×1014≈ 3.32×1016（次）答：它一天约能运算3.32×1016次.填空：
（1）x5 ·（ ）=　x 8
（2）a ·（ ）=　a6
（3）x · x3（ ）= x7
（4）xm ·（　 ）＝ｘ3m
x3a5 x3ｘ2m能力挑战:已知：am=2， an=3.
求am+n =？.动脑筋解： am+n = am · an
=2 × 3=6 通过本节课的学习，你有什么收获？ （1）、幂的符号法则，
负数的偶数次幂为正，负数的奇数次幂为负。

（2）、当底数是互为相反数时，
先根据数的乘方法则来确定幂的符号
符号运算：数学思想：链接幻灯片 18作业:
1 独立完成作业本和课本习题；
2 自编一道最能代表个人水平的题目,向与你水平相当的同学发出挑战。
3 整理同底数幂乘法的探索过程，写一篇小论文。
(选做题)
返回课堂小结把(a-b)看作一个整体指数相加