完全平方公式[下学期]

课件12张PPT。完全平方公式公式的结构特征:左边是a2 ? b2; 两个二项式的乘积,平方差公式应用平方差公式的注意事项:(a+b)(a?b)=即两数和与这两数差的积.右边是两数的平方差. 使用平方差公式(a+b)(a-b)=a2-b2 时，关键在于
找准_a__与_b__，公式左边积的两个因式中相同的
项看作a，互为相反数的项中带正号的项看作b。合作学习运用多项式与多项式相乘的法则计算下列各式
1）(a+2b)2
(2+x)2
(2a+x)2 = a2 + 4ab + 4b2
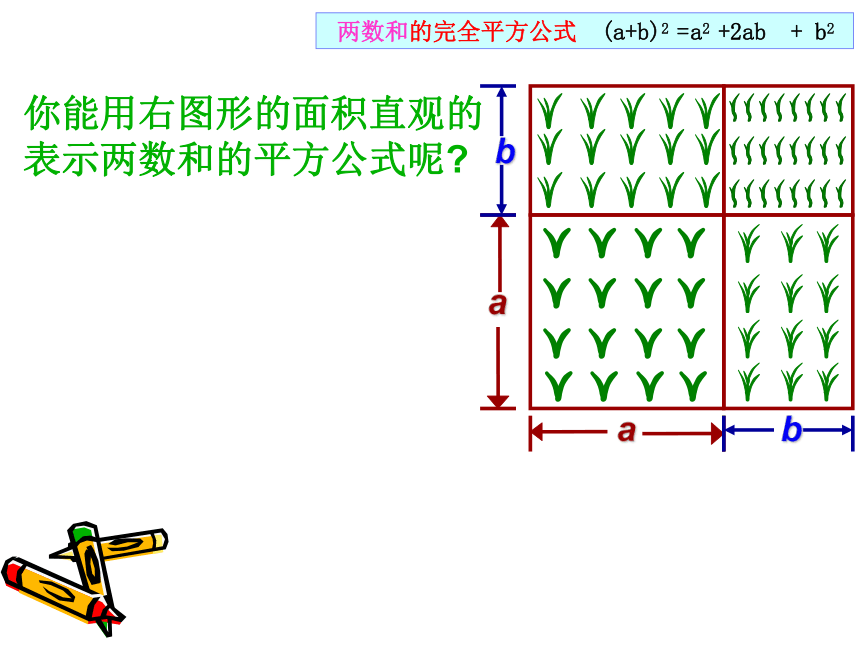
= 4 + 4x + x2= 4a2 + 4ax + x2 观察以上算式，你发现了什么规律？ (a+b)2=a2 +2ab+ b2两数和的完全平方公式即 两数和的平方,等于这两数
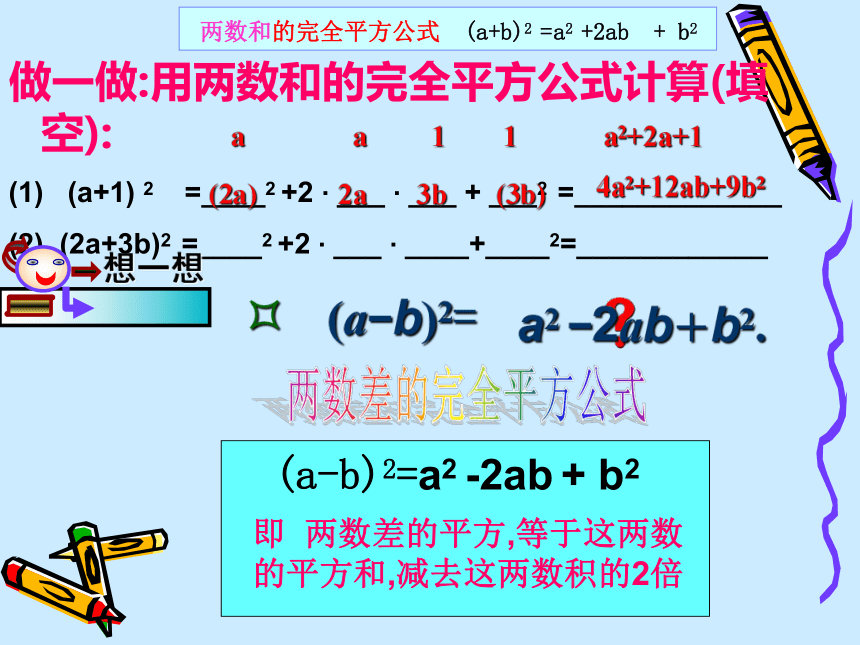
的平方和,加上这两数积的2倍你能用右图形的面积直观的表示两数和的平方公式呢? 两数和的完全平方公式 (a+b)2 =a2 +2ab+ b2做一做:用两数和的完全平方公式计算(填空):
(a+1) 2 =____2 +2 . ___ . ___ + ___2 =_____________
(2) (2a+3b)2 =____2 +2 . ___ . ____+____2=____________aa11a2+2a+1(2a)3b(3b)2a4a2+12ab+9b2a2 ?2ab+b2. 两数和的完全平方公式 (a+b)2 =a2 +2ab+ b2两数差的完全平方公式即 两数差的平方,等于这两数
的平方和,减去这两数积的2倍两数和的完全平方公式 (a+b)2 = a2+2ab+b2 .
两数差的完全平方公式 (a?b)2 = a2?2ab+b2 .比一比：这两个公式的区别与联系是什么?提示:
以上两个公式统称完全平 方公式.
平方差公式和完全平方公式也称乘法公式. 指出下列各式中的错误，并加以改正：
(1) (2a?1)2＝2a2?2a+1;
(2) (2a+1)2＝4a2 +1；
(3) (?a?1)2＝?a2?2a?1.解: (1)第一数被平方时, 未添括号;第一数与第二数乘积的2倍 少乘了一个2 ;应改为: (2a?1)2＝ (2a)2?2?2a?1+1; (2) 少了第一数与第二数乘积的2倍 (丢了一项);应改为: (2a+1)2＝ (2a)2+2?2a?1 +1; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号;第二数的平方 这一项错了符号;应改为: (?a?1)2＝(?a)2?2?(?a )?1+12; 纠 错 练 习(a+b)2 = a2+2ab+b2 .
(a?b)2 = a2?2ab+b2 . 例1 利用完全平方公式计算：
(1) (x+2y)2； (2) (2a-5)2;

(3) (-2s+t)2 ； (4) (-3x-4y)2.
使用完全平方公式与平方差公式的使用一样, 先把要计算的式子与完全平方公式对照, 明确哪个是 a , 哪个是 b.(a+b)2 = a2+2ab+b2 . (a?b)2 = a2?2ab+b2 .茶花是中国的传统名花之一 ，因其姿态优美，花形艳丽而受世人喜爱。茶花还是我们温州市的市花。例4 一花农有4块正方形茶花苗圃，边长分别为 30.1 m ，29.5m , 30 m , 27 m。现将这4块苗圃的边长都增加 1.5 m，求各苗圃的面积分别增加了多少m2 ？本节课你的收获是什么？小结本节课你学到了什么?注意完全平方公式和平方差公式不同：形式不同．结果不同：完全平方公式的结果 是三项，
即 (a ?b)2＝a2 ?2ab+b2;平方差公式的结果 是两项，
即 (a+b)(a?b)＝a2?b2. 有时需要进行变形，使变形后的式子符合应用完全平方公式
的条件，即为“两数和(或差)的平方”，然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2；第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键谢谢谢谢指导