5.4.1平方差公式上课[下学期]

课件24张PPT。义务教育课程标准实验教科书浙教版教材
（七年级下）5.4乘法公式
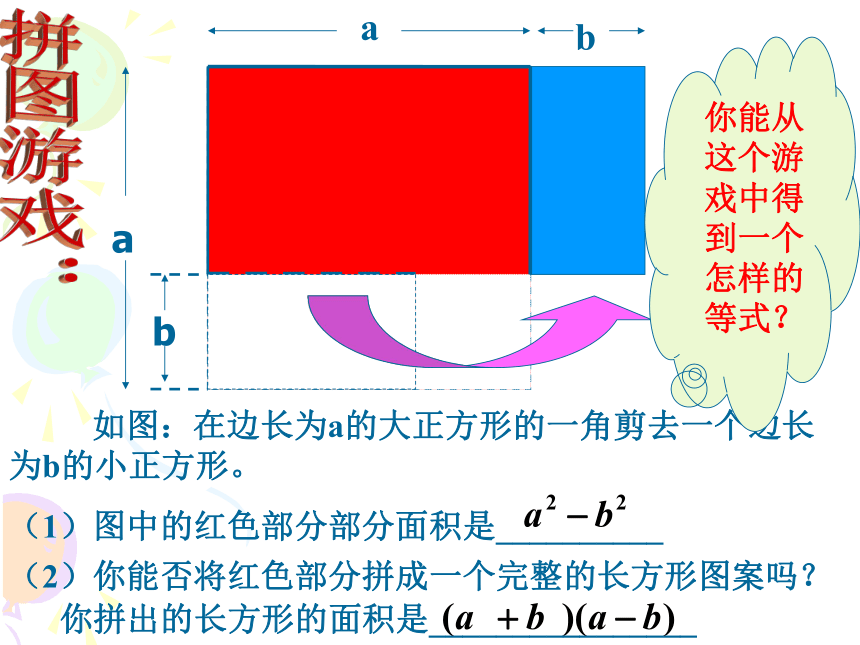
(1)钟中 张看谁算得快:(2) (x+3)(x?3) ；(3) (1+2a)(1?2a) ；(4) (x+4y)(x?4y) ；(1) (y+3)(y?5) ；=x2?9 ;=1?4a2 ;=x2?16y2 ;=y2?2y ? 15;你发现了什么规律？=x2?32 ;=12?(2a)2 ;=x2?(4y)2 ;两数和与这两数差的积,等于这两数的平方的差.大显身手拼图游戏： 如图：在边长为a的大正方形的一角剪去一个边长为b的小正方形。
（1）图中的红色部分部分面积是__________（2）你能否将红色部分拼成一个完整的长方形图案吗？你能从这个游戏中得到一个怎样的等式？你拼出的长方形的面积是________________
知识出击:2019-3-16概念挖掘:快言快语：参照平方差公式“(a+b)(a-b)=a2-b2”填空。(1) (t+s)(t-s)=____
(2) (1+n)(1-n)=_____ (3) (10+5)(10-5)=______t2-s212-n2102-52例1 运用平方差公式计算:
(1) (3x+5y)(3x-5y) =____2 – ____2 =________
(3x)(5y)9x2-25y2练习1:下列式子中哪些可以用平方差公式运算?如果可以,并计算.
⑴ (ab-8)(ab+8) ⑵⑶ (2+a)(a-2) ⑷ (3a+2b)(3a-2b)
⑸ (-4k+3)(-4k-3) ⑹ (1-x)(-x-1)
⑺ (-x-1)(x+1) ⑻ (x+3)(x-2)可以可以可以可以可以可以不可以不可以巩固拓展（一）应用公式：
2. 利用平方差公式计算（先确定各题的a与b，再填空）
(1)(5+6x)(5-6x)=( )2-( )2=__________
(2)(x-2y)(x+2y)=( )2-( )2=__________
(3)(-m+n)(-m-n)=( )2-( )2=__________
问题：利用平方差公式计算的关键是_________________
怎样确定a与b_________________________准确确定a和b符号相同的项是a,符号相反的项是b3 ?计算 (3a2-7)(-3a2-7)． 步骤：1、判断；2、调整；3、分步解。
（注意：要用好括号；幂的运算。）
解：原式=(-7+3a2)(-7-3a2)
＝(-7)2-(3a2)2
＝ 49-9a4．4、准确计算下列各式：
(1)(x2+4y)(x2-4y)
(2)(ap2+q2)(q2-ap2)
(3)(3a3-2b4)(2b4+3a3)
(4)(-1-3m)(1-3m)拓 展 练 习 运用平方差公式计算：
(?4a?1)(4a?1)． (用两种方法) ?运用平方差公式时，要紧扣公式的特征，
找出相等的“项”和符号相反的“项”，然后应用公式． (?4a?1)(4a?1)
==(?1)2 ?(4a)2 = 1?16a2。(?4a?1)(4a?1)= ?(4a+1) (?4a?1)(4a?1)= (4a)2 ?1??[ ] = 1?16a2。( ?4a?1 ) ( 4a ?1 )?1?4a?1+4a(4a+1) (4a?1)例2 用平方差公式计算:
103×97
(2)59.8×60.2=(100+3)(100-3)=1002-32=10000-9
=9991=(60-0.2)(60+0.2)=602-0.22
=3600-0.4
=3599.96王敏捷同学去商店
买了单价是9.8元/千克的糖果10.2千克，
售货员刚拿起计算器，王敏捷就说出应付99.96元，
结果与售货员计算出的结果相吻合。
售货员很惊讶地说：
“你好象是个神童，怎么算得这么快？”
王敏捷同学说：
“过奖了，我利用了在数学上刚学过的一个公式。”
你知道王敏捷同学用的是一个什么样的公式吗？
怎么计算的吗?(1)(x-y)(x+y)(x2+y2)
(2)已知 x2-y2=8 , x+y=-4 ，求x-y的值。(二)灵活应用公式1、基础训练：教材P.117,作业题。
2、扩展训练：利用平方差公式计算
(a+b+c)(a-b-c)运用平方差公式计算:运用平方差公式计算:5678×5680-56792=(5679-1)(5679+1)-56792=56792 -1 -56792= -1 利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216 一养鸡专业户改建一个边长为 a(m)的正方形养鸡场,计划纵向扩大3m,横向缩短3m,改建为长方形养鸡场.问改建后的养鸡场面积有没有变化?如果有变化,变化多少?原正方形的面积= a2
改建后的长方形的面积= (a+3)(a-3)=a2-9 (a+3)(a-3)-a2 = a2 -9-a2 =9如果A=1234567892,
B=123456788×123456790,
试比较A与B的大小. 若m,n为有理数,式子
的值与n有关吗?试说明理由.本节课你学到了什么?两数和与这两数差的积，等于它们的平方差。