平方差公式[下学期]
图片预览





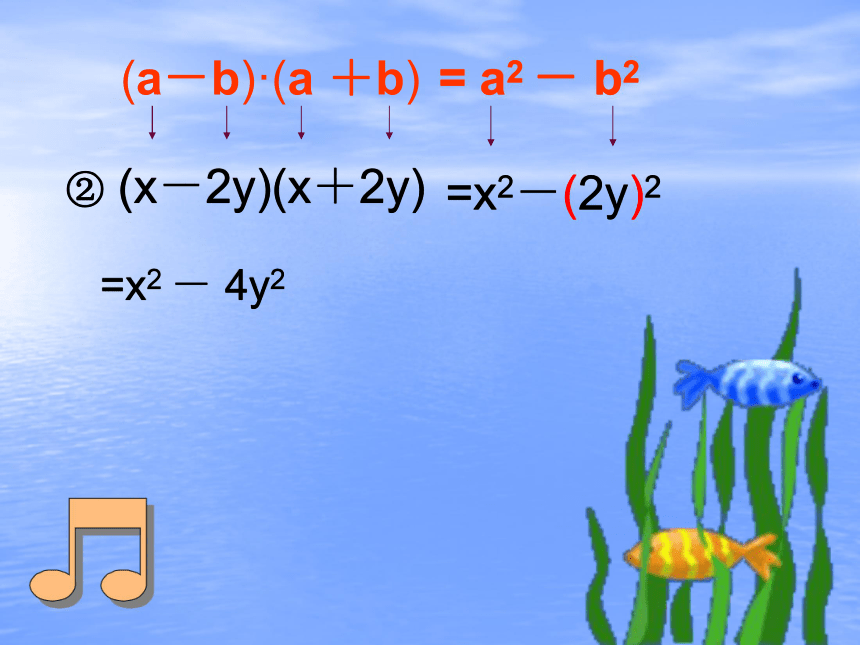
文档简介
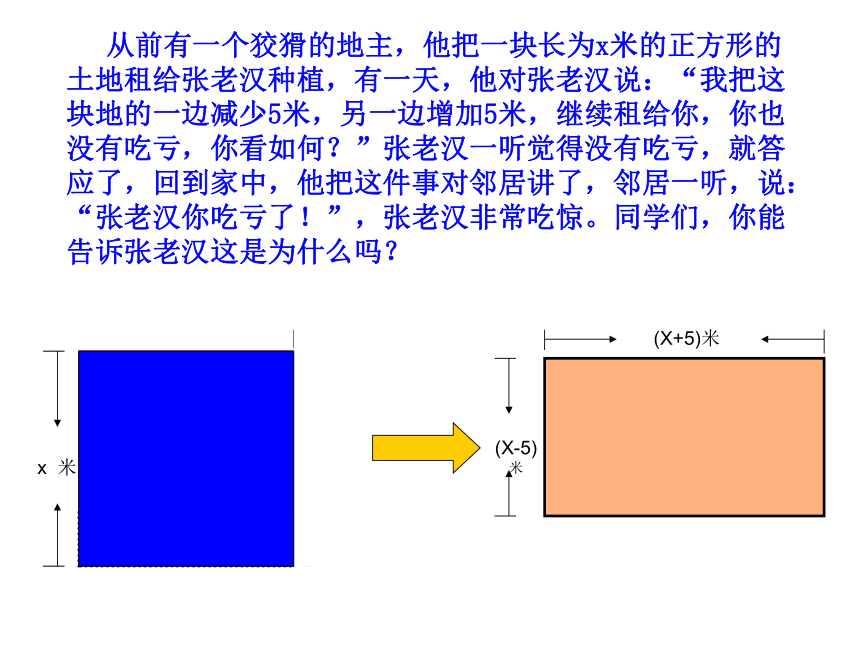
课件23张PPT。平方差公式 从前有一个狡猾的地主,他把一块长为x米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没有吃亏,你看如何?”张老汉一听觉得没有吃亏,就答应了,回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你吃亏了!”,张老汉非常吃惊。同学们,你能告诉张老汉这是为什么吗?猜测与探索1)( x+2)(x-2)
(1+3a)(1-3a)
(x+5)(x-5)
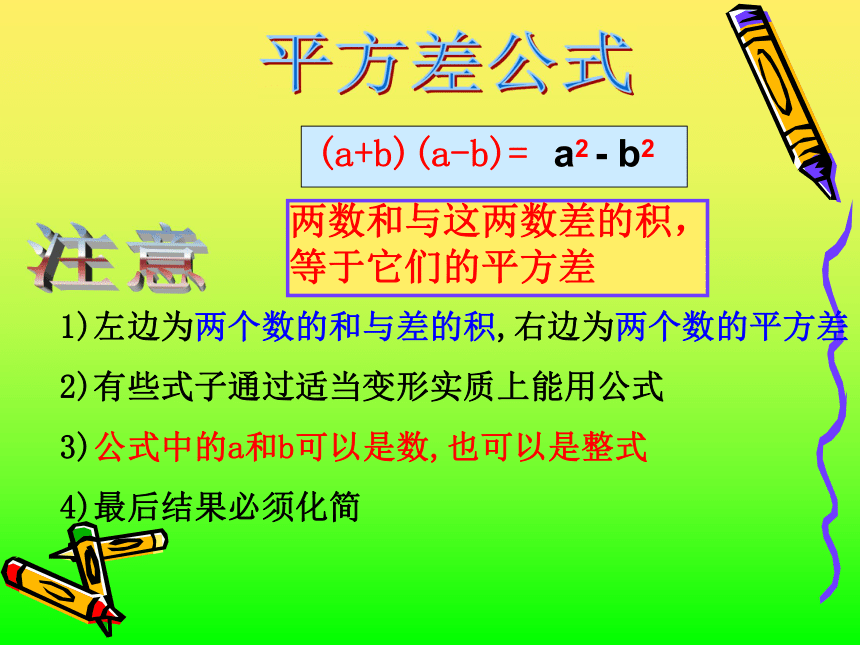
(y+3z)(y-3z)=x2=1=x2=y2-4-9a2-25 -9z2②(1 + 3a)( 1-3a)=1 -9a2③(m+ 5n)( m-5n)=m2 - 25n2④(3y + z)(3y-z)= 9y2 - z2①(x + 2)( x-2)=x2 - 41、它们的结果有什么特点?平方差的形式x2 - 2212-(3a)2m2 - (5n)2(3y)2 - z22、算式有什么特点?两个数的和乘以两个数的差3、能不能用字母表示你的发现?(a+b)(a-b)=a2-b2平方差公式 (a+b)(a-b)=a2- b2两数和与这两数差的积,等于它们的平方差注意1)左边为两个数的和与差的积,右边为两个数的平方差
2)有些式子通过适当变形实质上能用公式
3)公式中的a和b可以是数,也可以是整式
4)最后结果必须化简平方差公式:(a+b)(a-b)=a2-b2
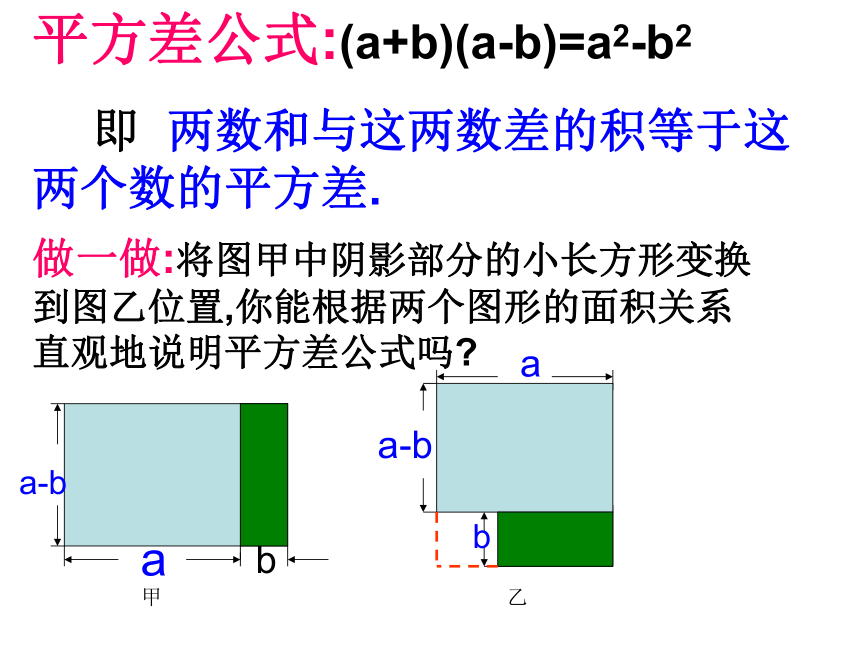
即 两数和与这两数差的积等于这两个数的平方差.做一做:将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系直观地说明平方差公式吗?
aba甲乙a-bba-b例 计算① (5+6x)(5-6x) ③ (8+ab)(-8+ab)
④ (-m+n)(-m-n)⑤ (-x-y)(x-y)② (x-2y)(x+2y)(a+b)·(a -b)= a2 - b2解:①(5+6x)(5-6x)= 52-(6x)2= 25-36x2 当“第一(二)数”是一分数或是数与字母的乘积时,要用括号把这个数整个括起来, 最后的结果又要去掉括号。 ② (x-2y)(x+2y)=x2-(2y)2=x2 - 4y2= a2 - b2(a-b)·(a +b)③ (8+ab)(-8+ab)
④ (- m+n)(- m-n)=(ab)2-82 = a2b2-64=(-m)2 -n2= m2 - n2⑤ (-x-y)(x-y)=(-y)2-x2=y2 - x2 平方差公式
两数和与这两数差的积,等于它们的平方差考一考下列多项式乘法中,能用平方差公式计算的是( )。A: (x+1)(1+x)B: ( a+b)(b- a)C: (-a+b)(a-b)D: (x2-y)(x+y2)E: (-a-b)(a-b)F: (c2-d2)(d2+c2)BEF1212(a+b)(a-b)=a2-b2
( )( )
×( )
×××判断下列各式是否正确,并说明理由( )( )√你认为怎样计算更简单?1、 59.8 × 60.22、 103 × 97解:59.8×60.2=(60-0.2)×(60+0.2)=3600-0.04=3599.96解:103×97=(100+3)×(100-3)=1002-32=10000-9=9991例3、先化简,再求值:(x-5)(x+5)(x2+25) ,其中x= - 3解:原式= (x2- 25)(x2+25)= (x2)2 – 252= x4 – 625当x= -3时, 原式=(-3)4-625= 81 - 625
= -5441.运用平方差公式计算:(2)5678×5680-567922.利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+13.(a+b+c)(a+b-c),是否可用平方差公式计
算?怎样应用公式计算?解: (a+b+c) (a+b-c)
= [(a+b)+c] [(a+b)-c]
= (a+b)2 - c2
= a2+2ab+b2 – c2拓 展 练 习(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 本题是公式的变式训练,以加深对公式本质特征的理解. 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 4.将下列各式变形为可利用平方差公式
计算的形式:
1) (a+2b+3)(a+2b-3)
2) (a+2b-3)(a-2b+3)
3) (a-2b+3)(a-2b-3)
4) (a-2b-3)(a+2b-3)
5) (3a-5b-2c)(-3a-5b+2c)
6) (x+y+m+n)(x+y-m-n)[(a+2b)+3][(a+2b)-3][a+(2b-3)] [a-(2b-3)][(a-2b)+3] [(a-2b)-3][(a-3)-2b] [(a-3)+2b][(-5b)+(3a-2c)] [(-5b)-(3a-2c)][(x+y)+(m+n)][(x+y)-(m+n)]4.下列各式哪些能用平方差公式计算?
怎样用?
1) (a-b+c)(a-b-c)
2) (a+2b-3)(a-2b+3)
3) (2x+y-z+5)(2x-y+z+5)
4) (a-b+c-d)(-a-b-c-d)本节课你的收获是什么?小结本节课你学到了什么?试用语言表述平方差公式 (a+b)(a?b)=x2?b2。应用平方差公式 时要注意一些什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式; 要利用加法交换律,对于不符合平方差公式标准形式者,来试试吧?解方程:
1、 (2x-3)(2x+3)=4x(x-2)
2、 y(2y+1)(2y-1)-2y(2y2-1)=4作 业 P谢谢谢谢指导
(1+3a)(1-3a)
(x+5)(x-5)
(y+3z)(y-3z)=x2=1=x2=y2-4-9a2-25 -9z2②(1 + 3a)( 1-3a)=1 -9a2③(m+ 5n)( m-5n)=m2 - 25n2④(3y + z)(3y-z)= 9y2 - z2①(x + 2)( x-2)=x2 - 41、它们的结果有什么特点?平方差的形式x2 - 2212-(3a)2m2 - (5n)2(3y)2 - z22、算式有什么特点?两个数的和乘以两个数的差3、能不能用字母表示你的发现?(a+b)(a-b)=a2-b2平方差公式 (a+b)(a-b)=a2- b2两数和与这两数差的积,等于它们的平方差注意1)左边为两个数的和与差的积,右边为两个数的平方差
2)有些式子通过适当变形实质上能用公式
3)公式中的a和b可以是数,也可以是整式
4)最后结果必须化简平方差公式:(a+b)(a-b)=a2-b2
即 两数和与这两数差的积等于这两个数的平方差.做一做:将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系直观地说明平方差公式吗?
aba甲乙a-bba-b例 计算① (5+6x)(5-6x) ③ (8+ab)(-8+ab)
④ (-m+n)(-m-n)⑤ (-x-y)(x-y)② (x-2y)(x+2y)(a+b)·(a -b)= a2 - b2解:①(5+6x)(5-6x)= 52-(6x)2= 25-36x2 当“第一(二)数”是一分数或是数与字母的乘积时,要用括号把这个数整个括起来, 最后的结果又要去掉括号。 ② (x-2y)(x+2y)=x2-(2y)2=x2 - 4y2= a2 - b2(a-b)·(a +b)③ (8+ab)(-8+ab)
④ (- m+n)(- m-n)=(ab)2-82 = a2b2-64=(-m)2 -n2= m2 - n2⑤ (-x-y)(x-y)=(-y)2-x2=y2 - x2 平方差公式
两数和与这两数差的积,等于它们的平方差考一考下列多项式乘法中,能用平方差公式计算的是( )。A: (x+1)(1+x)B: ( a+b)(b- a)C: (-a+b)(a-b)D: (x2-y)(x+y2)E: (-a-b)(a-b)F: (c2-d2)(d2+c2)BEF1212(a+b)(a-b)=a2-b2
( )( )
×( )
×××判断下列各式是否正确,并说明理由( )( )√你认为怎样计算更简单?1、 59.8 × 60.22、 103 × 97解:59.8×60.2=(60-0.2)×(60+0.2)=3600-0.04=3599.96解:103×97=(100+3)×(100-3)=1002-32=10000-9=9991例3、先化简,再求值:(x-5)(x+5)(x2+25) ,其中x= - 3解:原式= (x2- 25)(x2+25)= (x2)2 – 252= x4 – 625当x= -3时, 原式=(-3)4-625= 81 - 625
= -5441.运用平方差公式计算:(2)5678×5680-567922.利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+13.(a+b+c)(a+b-c),是否可用平方差公式计
算?怎样应用公式计算?解: (a+b+c) (a+b-c)
= [(a+b)+c] [(a+b)-c]
= (a+b)2 - c2
= a2+2ab+b2 – c2拓 展 练 习(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 本题是公式的变式训练,以加深对公式本质特征的理解. 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 4.将下列各式变形为可利用平方差公式
计算的形式:
1) (a+2b+3)(a+2b-3)
2) (a+2b-3)(a-2b+3)
3) (a-2b+3)(a-2b-3)
4) (a-2b-3)(a+2b-3)
5) (3a-5b-2c)(-3a-5b+2c)
6) (x+y+m+n)(x+y-m-n)[(a+2b)+3][(a+2b)-3][a+(2b-3)] [a-(2b-3)][(a-2b)+3] [(a-2b)-3][(a-3)-2b] [(a-3)+2b][(-5b)+(3a-2c)] [(-5b)-(3a-2c)][(x+y)+(m+n)][(x+y)-(m+n)]4.下列各式哪些能用平方差公式计算?
怎样用?
1) (a-b+c)(a-b-c)
2) (a+2b-3)(a-2b+3)
3) (2x+y-z+5)(2x-y+z+5)
4) (a-b+c-d)(-a-b-c-d)本节课你的收获是什么?小结本节课你学到了什么?试用语言表述平方差公式 (a+b)(a?b)=x2?b2。应用平方差公式 时要注意一些什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式; 要利用加法交换律,对于不符合平方差公式标准形式者,来试试吧?解方程:
1、 (2x-3)(2x+3)=4x(x-2)
2、 y(2y+1)(2y-1)-2y(2y2-1)=4作 业 P谢谢谢谢指导
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
