完全平方公式[下学期]

课件13张PPT。一.复习
1.叙述平方差公式的内容并用字母表示.
两个数的和与这两个数的差的积, 等于这两个数的平方差.
公式表示: (a+b) (a-b)=a2 –b2
2.（1）103× 97=（100+3)( 100-3）
3.计算:
(1) (a+b)2 (2) (a-b)2

2.计算:
(1) (a+b)2 (2) (a-b)2
解: (1) (a+b)2 = (a+b) (a+b)
= a2 +ab+ab+b2
= a2 +2ab +b2
(2) (a-b)2 =(a-b) (a-b)
=a2-ab-ab+b2
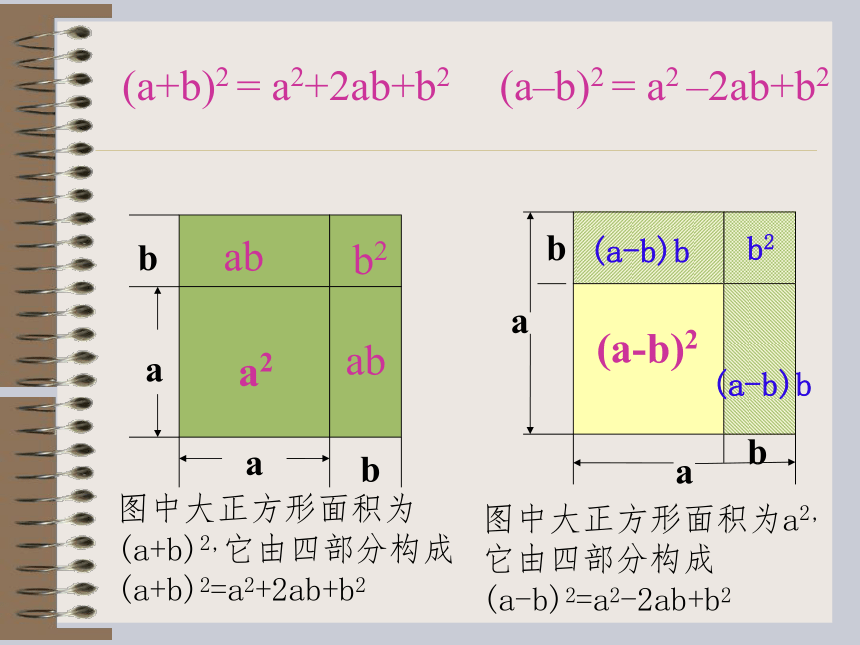
=a2-2ab+b2你能用面积的方法得出上式吗？ (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
图中大正方形面积为(a+b)2,它由四部分构成(a+b)2=a2+2ab+b2图中大正方形面积为a2,它由四部分构成 (a-b)2=a2-2ab+b2
(a-b)b(a-b)bb2完全平方公式:
(a+b)2 = a2+2ab+b2
(a–b)2 = a2 –2ab+b2
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.公式的结构特征 (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2 左边:两数和(或差)的平方 右边:这两数的平方和,加上(或减去)它们的积的2倍. 公式中的字母a,b可以是数,也可以是单项式或多项式.例如:计算 (x+2y)2,(2x-3y)2.(2x-3y)2=(x+2y)2=x2+4xy+4y2=4x2-12xy+9y2(2x)2-2?2x?3y+(3y)2
由上可以看出应用公式的关键是： （一）是否能用
（二）确定题目中谁是a,谁是b例1.运用完全平方公式计算:(1) (- 4a+b)2 (2)(-y- )2例1.运用完全平方公式计算:(1) (- 4a+b)2 (2)(-y- )2 =(-4a)2+2?(-4a)?b+b2
解:(1)(-4a+b)2=16a2-8ab+b2例1.运用完全平方公式计算:(1) (4a-b)2 (2)(-y- )2 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b2哪一部分相当于公式里的a，哪一部分相当于公式里的b呢？例1.运用完全平方公式计算:(1) (4a-b)2 (2)(-y- )2 =(4a)2-2?4a?b+b2
(2)(-y- )2解:(1)(4a-b)2=16a2-8ab+b2 =1002+2×100×３+３2
(2) 1992 =(200-1)2解:(1) 10３2 =(100+３)2=10000+400+9=10 409=2002-2200+12例2.运用完全平方公式计算:(1) 10３2 ; (2)1992=40000-400+1=39601巩固练习:
1.下列各式哪些可用完全平方公式计算 (1)(2a-3b)(3b-2a)
(2)(2a-3b)(-3b-2a)
(3)(-2m+n)(2m+n)
(4)(2m+n)(-2m-n) 2.错例分析：
(1)（a+b)2=a2+b2
(2)(a-b)2=a2-b2小结：1.本节课主要学习了完全平方公式:
(a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
说出公式中a,b的含义2.怎样正确运用完全平方公式：
计算时，要先观察题目特点是否符合公式的条件，若不符合，应先变形为符合公式的条件的形式，再利用公式进行计算，若不能变为符合公式条件的形式，则应运用乘法法则进行计算．