第一章平行线导学案

七年级（下）数学导学案第一章
1.1平行线
【课前预习导学】
1.两条直线相交只有 个交点.
2.如图，直线AB、CD交于点O，OE、OF是过O点的两条射线，
其中构成对顶角的是（ ）
A.∠AOF与 ∠DOE B.∠EOF与∠BOE
C.∠BOC与∠AOD D.∠COF与∠BOD
3. 下列说法中正确的个数有（ ）
（1）直线外一点与直线上各点连接的所有线段中垂线段最短.
（2）过直线外一点，画这条直线的垂线段可以画无数条.
（3）过直线外一点，能画一条,且只能画一条直线和已知直线垂直.
（4）直线外一点到这条直线的垂线段叫做点到直线的距离.
A.1个 B.2个 C.3个 D.4个
4. 过直线AB外一点N，画AB的垂线.
5. 如图，直线AD和BE相交于O点，CO⊥AD，∠COD=90度，∠COE=70度，求∠AOB的度数.
【课外资料导学】
“几何”这一名词最早出现于希腊，由希腊文“土地”和“测量”二字合成，意思是“测地术”。古希腊学者认为，几何学原是由埃及人开创的，由于尼罗河泛滥，常把埃及人的土地界线冲掉，于是他们每年要作一次土地测量，重新划分界线。这样，埃及人逐渐形成一种专门的测地技术，随后这种技术传到希腊，逐步演变成现在狭义的几何学.
【课中生成导学】
1.在同一平面内，两条直线的位置关系有哪几种？
2.经过一点，可作几条直线与已知直线平行？
得 分
【课堂测评导学】(共10分)
1.下列命题：
（1）长方形的对边所在的直线平行；（2）经过一点可作一条直线与已知直线平行；（3）在同一平面内，如果两条直线不平行，那么这两条直线相交；（4）经过一点可作一条直线与已知直线垂直．其中正确的个数是（ ）
A．1 B．2 C．3 D．4
2．过直线AB外一点P，画AB的平行线.
3. 如图，长方体ABCD-EFGH，
（1）图中与棱AB平行的棱有哪些？
（2）图中与棱AD平行的棱有哪些？
（3）连接AC、EG，问AC、EG是否平行.
4.请画一个平行四边形，其中较小的内角为45度.
【课后拓展导学】
平面内有若干条直线，当下列情形时，可将平面最多分成几部分.
（1）有一条直线时，最多分成2部分.
（2）有两条直线时，最多分成2+2部分.
（3）有三条直线时，最多分成 部分.
……
（4）有n条直线时，最多分成 部分.
1.2同位角、内错角、同旁内角
【课前预习导学】
1.在同一平面内，两直线有哪些位置关系？
2.两条直线相交产生_______个角（平角除外），请你画出来，并说明它们之间有怎样的关系？
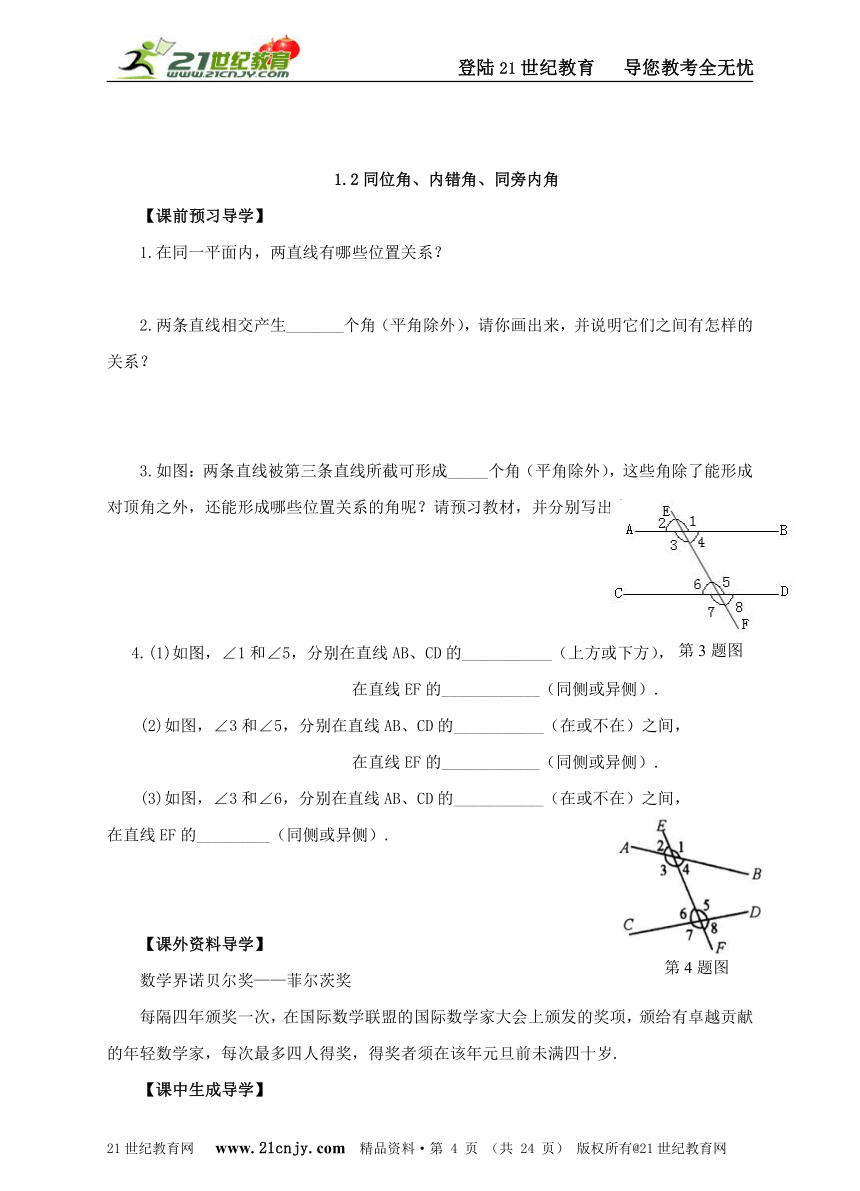
3.如图：两条直线被第三条直线所截可形成_____个角（平角除外），这些角除了能形成对顶角之外，还能形成哪些位置关系的角呢？请预习教材，并分别写出来.
4.(1)如图，∠1和∠5，分别在直线AB、CD的___________（上方或下方），
在直线EF的____________（同侧或异侧）.
如图，∠3和∠5，分别在直线AB、CD的___________（在或不在）之间，
在直线EF的____________（同侧或异侧）.
如图，∠3和∠6，分别在直线AB、CD的___________（在或不在）之间， 在直线EF的_________（同侧或异侧）.
【课外资料导学】
数学界诺贝尔奖——菲尔茨奖
每隔四年颁奖一次，在国际数学联盟的国际数学家大会上颁发的奖项，颁给有卓越贡献的年轻数学家，每次最多四人得奖，得奖者须在该年元旦前未满四十岁.
【课中生成导学】
寻找同位角、内错角、同旁内角，一定要在三线八角中，请你画出三线八角这个基本图形.
请你在上题的图形中，寻找出八个角，并找出同位角、内错角、同旁内角.
得 分
【课堂测评导学】(共10分)
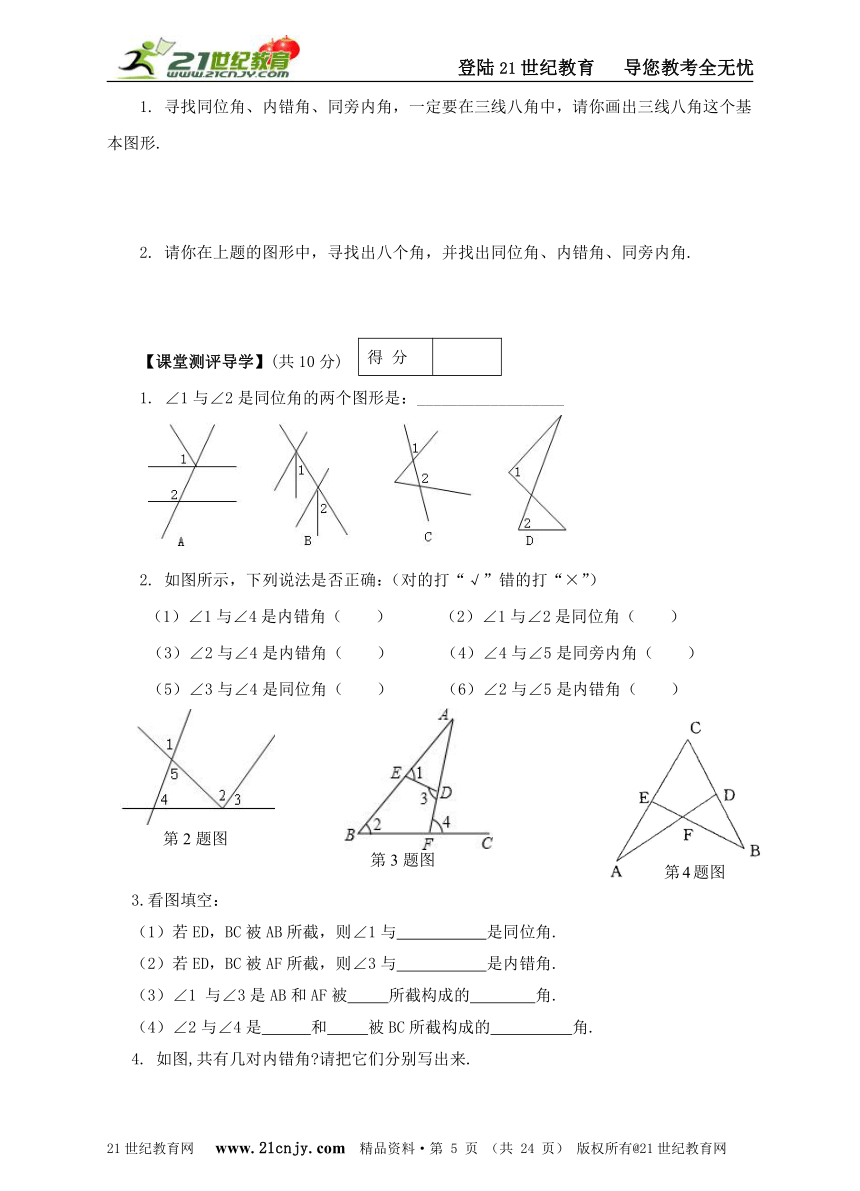
1. ∠1与∠2是同位角的两个图形是：__________________
2. 如图所示，下列说法是否正确：（对的打“√”错的打“×”）
（1）∠1与∠4是内错角（ ） （2）∠1与∠2是同位角（ ）
（3）∠2与∠4是内错角（ ） （4）∠4与∠5是同旁内角（ ）
（5）∠3与∠4是同位角（ ） （6）∠2与∠5是内错角（ ）
3.看图填空：
（1）若ED，BC被AB所截，则∠1与 是同位角.
（2）若ED，BC被AF所截，则∠3与 是内错角.
（3）∠1 与∠3是AB和AF被 所截构成的 角.
（4）∠2与∠4是 和 被BC所截构成的 角.
4. 如图,共有几对内错角?请把它们分别写出来.
5.如图所示，已知∠1的同旁内角等于57°，求∠1的内错角的度数.
【课后拓展导学】
观察图形，图中共有____对同位角、____对内错角、____对同旁内角，并把它们分别写出来：
1.3平行线的判定（1）
【课前预习导学】
1. 如图所示，下列说法是否正确：（对的打“√”错的打“×”）
①∠1和∠B是同位角 （ ）
②∠2和∠B是同位角； （ ）
③∠2和∠C是内错角； （ ）
④∠EAD和∠C是内错角； （ ）
2．下列说法正确的是（ ）
A．经过一点有且只有一条直线与已知直线平行
B．经过一点有无数条直线与已知直线平行
C．经过一点有一条直线与已知直线平行
D．经过直线外一点有且只有一条直线与已知直线平行
3.如图，直线a，b被直线c所截，形成的8个角中，你能找出几对同位角？[来源:Zxxk.Com]
4.若∠1=∠2，可推出∠1与∠ADE______________；
5.如图，直线AB，CD被DE所截，则∠1和 是同位角，∠1和 是内错角，∠1和 是同旁内角．如果∠5=∠1，那么∠1 ∠3．
6. 若∠1=∠2，试说明：∠3与∠4是互为补角.
【课外资料导学】
欧几里得　古希腊数学家，凭借所著的《几何原本》（简称《原本》）而闻名于世.他一生治学严谨.所著的《几何原本》共13卷，是世界上最早公理化的数学著作，影响着历代科学文化的发展和科技人才的培养.
【课中生成导学】
本节课所学的判定两条直线平行的方法是什么？请画出图形，并用几何语言表述.
得 分
【课堂测评导学】(共10分)
1. 如图，∠2=130°，∠3=50°，则∠1=______，____∥____，理由___________________.
2.如图，下列各组等式中，不能判定a∥b的是 ( )
A．∠2 =∠4 B．∠1 =∠3 C．∠3 =∠4 D．∠1 =∠4
3.如图，下列判断中正确的是( )
A．若∠1 =∠2，则a∥b B．若∠1 =∠3，则m∥n
C．若∠2 =∠4, 则a∥b D．若∠1 =∠2，则m∥n
4.如图所示．若∠AEC= 100°，则∠D=_______度时，AB∥DF．
5. 如图，∠A=∠B，CD是△ABC的外角平分线，那么AB∥CD吗?为什么?
【课后拓展导学】
如图，∠1=∠2，DE⊥AB，CF⊥AB，判断FG和BC是否平行，
并说明你的理由．
1.3平行的判定（2）
【课前预习导学】
1. 我们已经学过的判定两条直线平行的方法有那几个？
2．如图所示，直线DE交∠ABC的边BA于点D，∠B=70°，
若∠ADE的度数等于　　　　，才能使得DE∥BC．
3.∠1，∠2，∠3，∠4，∠5，∠6，∠7，∠8是直线 、 被第三条直线 所截而成的.在这六个角中：
（1）∠3的内错角是 ，∠2的内错角是 .
（2）∠6的同旁内角是 ，∠5的同旁内角是 .
4．若∠与∠是同位角，且∠=50°，则∠的度数是（ ）
A．50° B．130° C．50°或130° D．不能确定
5. 如图所示，截直线DE、射线BC被直线AB所截，
（1）若∠1=∠2=70o，则∠4=________；
（2）若∠1+∠3=180o，∠1=70o，则∠4=________；
6.如图所示，直线AB、CD被直线EF所截
（1）∠l与∠2，∠1与∠3，∠3与∠4各是什么关系的角？
（2）如果∠1＝∠2，那么∠2和∠3相等吗？∠4和∠3互补吗？为什么？
【课外资料导学】
丘成桐 著名华裔数学家，哈佛大学终身教授，美国科学院院士，中国科学院外籍院士，数学界最高荣誉菲尔兹奖得主，克拉福德奖得主，获得有数学家终身成就奖之称的沃尔夫数学奖.
【课中生成导学】
写出判定两条直线平行的方法，并画出图形，用几何语言表述.


得 分
【课堂测评导学】(共10分)
如图所示,如果∠3=∠7,或 ,
那么 ,理由是 ；
如果∠5=∠3,或_______,
那么________, 理由是 ；
如果∠2+ ∠5= ______ 或者___ ___,
那么∥,理由是_____ _____.
2. 下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
3. 如图所示，完成下列填空：
①如果∠1=∠C，可得ED∥ .
②如果∠2=∠BED，可得DF∥ .
③如果∠2＋∠AFD=180o，可得 .
4. 如图所示：
∵AC⊥AB，BD⊥AB（已知）
∴∠CAB＝90°，∠______＝90°（ ）
∴∠CAB＝∠______
∵∠CAE＝∠DBF（已知）
∴∠CAB—∠CAE=∠_____—∠______
即∠BAE＝∠______
∴_____∥_____（ ， ）
5. 如图：∠1=，∠2=，∠3=，
试说明直线AB与CD，BC与DE的位置关系.
【课后拓展导学】
如图所示,已知直线，，，，且∠1=∠2,∠3+∠4=180°，
则a与c平行吗?为什么?
1.4 平行线的性质（1）
【课前预习导学】
1.如图，直线AB、CD被直线EF所截，交于点G、H.若∠EGB=∠GHD，则平行线有 .
2.如图，直线AB∥CD，直线EF分别交AB、CD于点E、F.
（1）测量同位角：在图（1）中，∠EGB= °，∠GHD = °；
在图（2）中，∠EGB= °，∠GHD = °；
（2）发现结论：由上面的测量结果，你发现什么结论？
（3）利用结论：填空：
①如图，DE∥BC，且∠ADE=62°，∠C=65°，则∠B= °，则∠AED= °.
②如图，直线∥，若∠1=50°，则∠3= °，∠2= °.

③如图，直线AB∥CD，若∠2=2∠1，则∠1= °，则∠2= °.
【课外资料导学】
欧几里得平行公理简称欧氏平行公理．对于任意直线a及不在a上的一点A，那么在a和A确定的平面上，通过A点至多有一直线与直线a不交．这里，共面不交就是平行，所以欧氏平行公理确定了直线间的平行关系．这种关系叙述为“某某直线平行于某某直线”．
【课中生成导学】
1.平行线的性质： .
画出图形： 几何语言表述：
2.在同一平面内，垂直于同一直线的两条直线互相平行.
如图，直线⊥直线，直线⊥直线，则直线∥.
3.平行线的性质：“两直线平行，同位角相等”.
--------说明两个角相等的常用方法.
得分
【课堂测评导学】（10分）
1.一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度是（　　）
A．第一次右拐50°，第二次左拐130° B．第一次左拐50°，第二次右拐130°
C．第一次左拐50°，第二次左拐130° D．第一次右拐50°，第二次左拐50
2.已知：如图，AB∥DE，∠E=65°，则∠B+∠C的度数是（ ）
A．135° B．115° C．65° D．35°
3.同一平面内有四条直线a、b、c、d，若a∥b，a⊥c，b⊥d，则
直线c、d的位置关系为（ ）
A．互相垂直 B．互相平行 C．相交 D．无法确定
4.如图，AB∥CD，EG⊥AB，垂足为G，若∠1=50°，则∠E= .
5.如图，已知BE平分∠ABC，∠1=∠2，∠C=70o，求∠AED的度数.
【课后拓展导学】
如图，在折线ABCDEFG中，已知∠1=∠2=∠3=∠4=∠5，延长AB、GF交于点M．试探索∠AMG与∠3的关系，并说明理由．
1.4 平行线的性质（2）
【课前预习导学】
1.如图，直线AB∥CD，并被直线EF所截，请回答下列问题：
（1）填空：∠1 ∠2，∠1 ∠3.（＞，＝，＜）；∠2与∠3是一对 角，∠3与∠4是一对 角.
（2）思考：∠2与∠3相等吗？请说明理由.
（3）思考：∠3与∠4有怎样的数量关系？请说明理由.
（4）归纳：通过（2）（3），你可以得到什么结论？
2.利用以上得到的结论，填空：
（1）如图，AB∥CD，AD和BC相交于点O，∠A=40°，∠B=75°．则∠C= °，∠D= °.
（2）如图，直线AB、CD相交于点E，DF∥AB．若∠D=70°，则∠AED= °.
（3）如图，DE∥AB，若∠A=55°，则∠ACD= °，∠ACE= °.
（4）如图，已知AB∥CD，∠1 = 100°，则∠2 = ，∠3 = ，∠4 = ．
【课外资料导学】
古希腊大数学家欧几里德是与他的巨著——《几何原本》一起名垂千古的.这本书是世界上最著名、最完整而且流传最广的数学著作，也是欧几里德最有价值的一部著作.在《原本》里，欧几里德系统地总结了古代劳动人民和学者们在实践和思考中获得的几何知识，欧几里德把人们公认的一些事实列成定义和公理，以形式逻辑的方法，用这些定义和公理来研究各种几何图形的性质，从而建立了一套从公理、定义出发，论证命题得到定理得几何学论证方法，形成了一个严密的逻辑体系——几何学.
【课中生成导学】
1.平行线的两个性质是： ；
.
画出图形： 几何语言表述：
2.平行线的性质“两直线平行，内错角相等”.--------说明两个角相等的常用方法.
3. 平行线的性质“两直线平行，同旁内角互补”.--------说明两个角互补的常用方法，同时可以利用“同角或等角的补角相等”说明两个角相等.
得分
【课堂测评导学】（10分）
1.如图，AB∥CD，那么（ ）
A．∠1=∠4 B．∠1=∠3 C．∠2=∠3 D．∠2=∠4
2.如图，AD∥BC，AB∥CD，下列各式不一定正确的是（ ）
A．∠1+∠2=180° B．∠2+∠3=180° C．∠3+∠4=180° D．∠2+∠4=180°
3.如图，AB∥EF，BC∥DE，则∠E+∠B的度数为________．
4.如图，直线∥，∠3的度数是∠1度数的2倍，则∠2的度数是 °.
5.如图，已知：∠1=∠2，∠D=50°，求∠B的度数.
【课后拓展导学】
如图，已知∠ABE +∠DEB = 180°，∠1 =∠2，请说明∠F =∠G的理由．
1.5 图形的平移
【课前预习导学】
1.观察下列汽车标志的图片：

这些图片给我们一种图形的 现象.
2.观察下面四幅图片：

你认为是四幅图片有什么共同的特点？
3.观察右图网格图中的两个三角形，回答下列问题：
（1）相等的线段有 ；
（2）相等的角有 ；
（3）平行的线段有 .
4.将方格图中的三角线按下列平移要求，画出相应的图形：
（1）将三角形向右平移两格；
（2）将三角形向下平移三格；
（3）将三角形先向下平移两格，再向右平移三格.
【课外资料导学】
在几何学发展的历史中，欧几里得的《几何原本》起了重大的历史作用.这?种作用归结到一点，就是提出了几何学的“根据”和它的逻辑结构的问题.在他写的《几何原本》中，就是用逻辑的链子由此及彼的展开全部几何学，这项工作，前人未曾作到.《几何原本》的诞生，标志着几何学已成为一个有着比较严密的理论系统和科学方法的学科.
【课中生成导学】
1.图形平移的性质：
2.图形的平移不改变图形的 ，图形上的每一个点都沿同一个方向移动相同的距离，但图形的 发生改变.
3.图形的平移有两个要素：一是图形平移的 ，二是图形平移的 .
4.平移要确定一个图形平移后的位置所需条件为：①图形原来的位置；②平移的方向；③平移的距离．
得分
【课堂测评导学】（10分）
1.如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（　 　）
A． B． C． D．
2.如图，哪一个选项的右边图形可由左边图形平移得到（　　 ）
A． B． C． D．
3.有以下现象：①温度计中液柱的上升或下降；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动，其中，属于平移的是（　　 ）
A．①② B．①③ C．②③ D．②④
4.如图△ABC沿着PQ的方向平移到△A′B′C′位置，
则AA′∥_________∥__________；
AA′=________ = ________；AB=________，∠A=_______.
5.已知△ABC，画出△ABC沿 PQ方向平移2cm后的△A′B′C′．
【课后拓展导学】
如图所示是重叠的两个直角三角形．将其中一个直角三角形沿BC方向平移得到△DEF．如果AB=8cm，BE=4cm，DH=3cm，求图中阴影部分的面积.
参考答案
1.1平行线
【课前预习导学】
1.1 2.C 3.B 4.略 5. ∠AOB=20°
【课中生成导学】
1. 平行 相交
2. 1条
【课堂测评导学】
1.C 2．略 3.(1)EF DC HG (2)BC EH FG (3)平行 4略.
【课后拓展导学】
（4）
1.2同位角、内错角、同旁内角
【课前预习导学】
1.相交或平行 2.4 相等或互补 3. 8，同位角、内错角、同旁内角 4.（1）上方，同侧（2） 在，异侧（3）在，同侧
【课中生成导学】
略
【课堂测评导学】
1.B C 2．(1) ×(2) √(3) ×(4) √(5) √(6) √ 3.(1) ∠2(2) ∠4(3)ED 内错角（4）AB AF 同位角 4. 6对 略 5.123°
【课后拓展导学】
5,6,7
1.3平行线的判定（1）
【课前预习导学】
1. (1) √(2) × (3) √ (4) × 2.D 3.4对 4.相等 5. = 6.略
【课中生成导学】
两条直线被第三条直线所截，如果同位角相等，那么两条直线平行
在同一平面内，垂直于同一条直线的两条直线互相平行
画图(略) 符号语言表述（略)
【课堂测评导学】
50°，，同位角相等，两直线平行 2．C 3.D 4. 80°5.平行，略
【课后拓展导学】
平行 略
1.3平行线的判定（2）
【课前预习导学】
1.同位角相等，两直线平行 垂直于同一条直线的两条直线平行 2.70° 3.（1）∠5，∠6（2）∠3，∠2 4.D 5.（1）70°（2）70° 6.（1）∠1与∠2是同位角，∠1与∠3是对顶角，∠3与∠4是同旁内角（2）相等，互补
【课中生成导学】
略
【课堂测评导学】
1. ∠2=∠8 a//b 同位角相等，两直线平行 ∠2=∠6 a//b 内错角相等，两直线平行 ∠3+∠6=180° 同旁内角互补等，两直线平行
2．B 3.(1)AC (2)AB (3)AC//DE. 4. ∠ABD 垂直的定义 ∠ABD ∠DBF ∠ABF
AE//BF 内错角相等，两直线平行 5. AB//CD BC//DE
【课后拓展导学】
a//c
1.4 平行线的性质（1）
【课前预习导学】
1.AB∥CD； 2.（1）略，（2）两直线平行，同位角相等，（3）① 62°，65°；② 130°，130°；③60°，120°.
【课中生成导学】
1.两直线平行，同位角相等
【课堂测评导学】
1.D； 2.C； 3.B； 4. 40°；5. 70°.
【课后拓展导学】
∠AMG ＝∠3（理由略）
课后练习
1.70°； 2. 40°，40°； 3.44； 4.B； 5.B； 6.B； 7.C； 8.B； 9.D； 10.B； 11. C； 12.略； 13.∠EAB=50°；14. ∠1=75°，∠2=105°.
1.4 平行线的性质（2）
【课前预习导学】
1.（1）＝，＝，内错，同旁内，（2）∠2＝∠3（理由略），（3）∠3+∠4＝180°（理由略）；（4）两直线平行，内错角相等；两直线平行，同旁内角互补. 2. （1）75°，40°； （2） 110°； （3）55°，125°； （4）100°，100°，80°.
【课中生成导学】
1.两直线平行，内错角相等；两直线平行，同旁内角互补.
【课堂测评导学】
1.D； 2.D； 3. 180°； 4. 120°；5. 130°.
【课后拓展导学】
（理由略）
课后练习
1.110°； 2. 110°； 3.72； 4.56°； 5.①②③④； 6.A； 7.B； 8.B； 9.B； 10.C； 11. 134°； 12. 115°； 13.略； 14. ∠AED=∠ACB.
1.5 图形的平移
【课前预习导学】
1.平移； 2.都可以看成是由某一图形进行平移得到整个图形； 3.（1）AB＝EF，BC＝ED，AC＝FD，（2）∠A＝∠F，∠B＝∠E，∠C＝∠D，（3）AB∥EF， BC∥ED，AC∥DF； 4.（图略）.
【课中生成导学】
1.平移不改变图形的形状和大小.一个图形和它经过平移所得的图形中，两组对应点的连线平行（或在同一直线上）且相等. 2.形状和大小，位置；3.方向，距离.
【课堂测评导学】
1.D； 2.C； 3. D； 4. BB′，CC′；BB′，CC′；A′B′，∠A′；5. 图略.
【课后拓展导学】
∵△ABC平移到△DEF，∴AB=DE, =，
∵=+ ，=+，
∴===（5+8）×4=26.
课后练习
1.5； 2. 52°，10°； 3. ④； 4.9； 5.540； 6.B； 7.A； 8.B； 9.B； 10.B； 11. C； 12.D； 13.略； 14. 略； 15.（1）3，（2）1或5.