第一章平行线复习基础运用篇课件

(共34张PPT)
新浙教版数学七年级（下）
第一章平行线复习基础运用篇
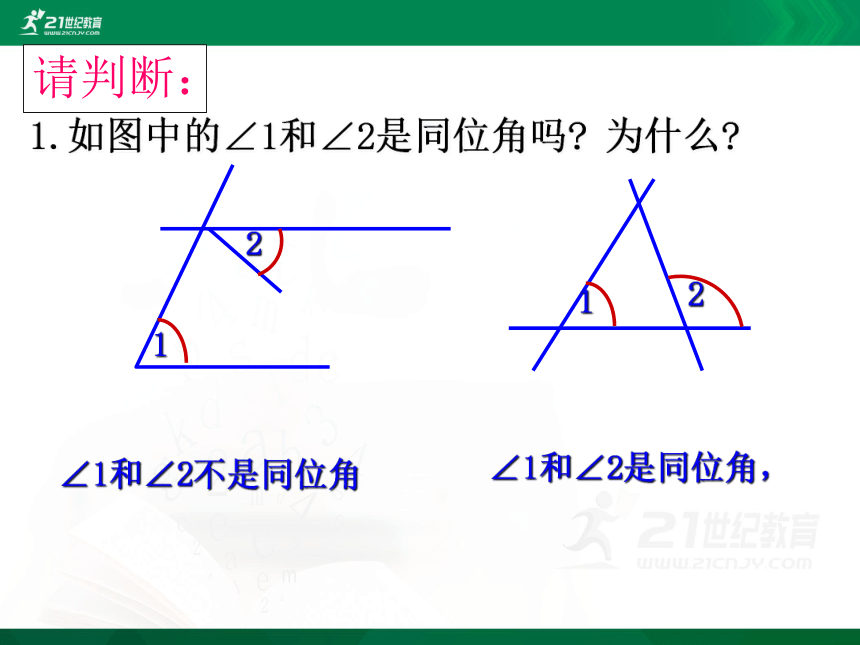
∠1和∠2不是同位角
请判断：
1.如图中的∠1和∠2是同位角吗 为什么
1
2
1
2
∠1和∠2是同位角，
1
2
3
4
5
6
7
8
a
b
c
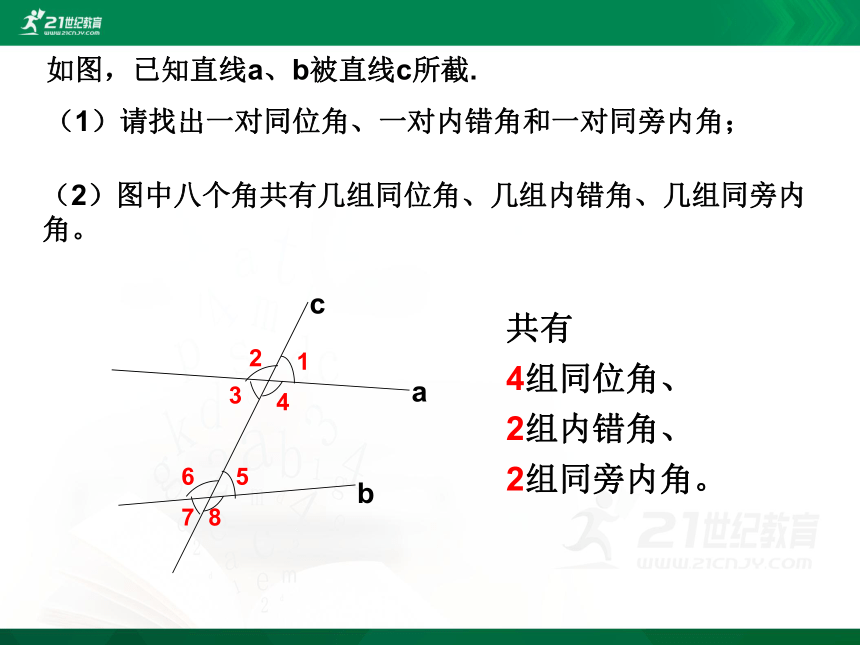
如图，已知直线a、b被直线c所截.
（1）请找出一对同位角、一对内错角和一对同旁内角；
（2）图中八个角共有几组同位角、几组内错角、几组同旁内角。
共有
4组同位角、
2组内错角、
2组同旁内角。
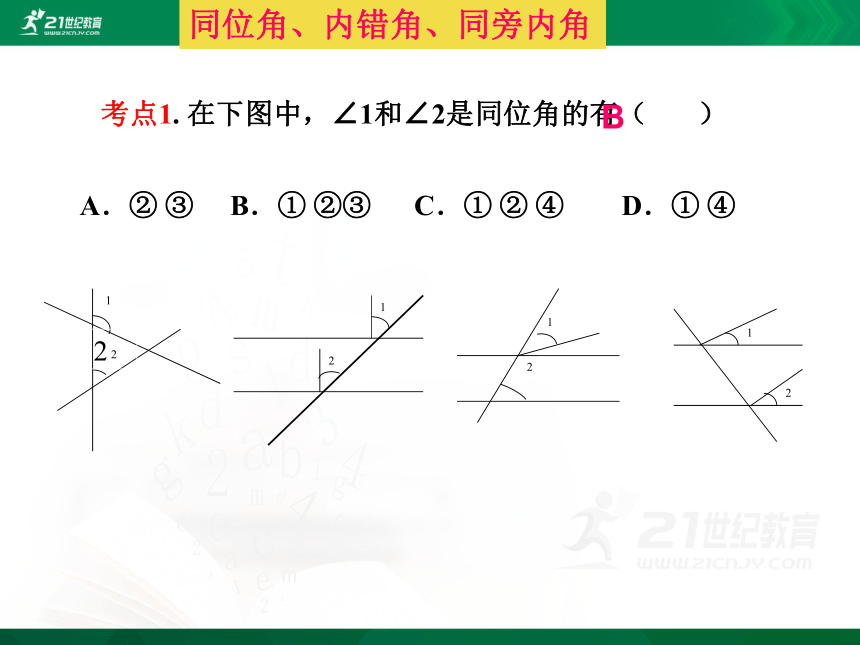
考点1. 在下图中，∠1和∠2是同位角的有（ ）
A．② ③ B．① ②③ C．① ② ④ D．① ④
1
2
1
2
同位角、内错角、同旁内角
B
2
1
1
2
2
2.找出图中的同位角、内错角、同旁内角
(只限用数字表示的角)
图①中同位角有: ∠1与∠3, ∠6与∠3
内错角有: ∠1与∠4, ∠4与∠6
同旁内角有: ∠1与∠2, ∠5与∠6
3.图②中同位角有: ∠1与∠4,
内错角有: ∠1与∠7, ∠3与∠6 ,∠2与∠5
同旁内角有: ∠2与∠7, ∠7与∠6,
∠2与∠6, ∠3与∠5,
∠3与∠4, ∠4与∠5
练习
6
5
4
3
2
1
图①
7
6
5
4
3
2
1
图②
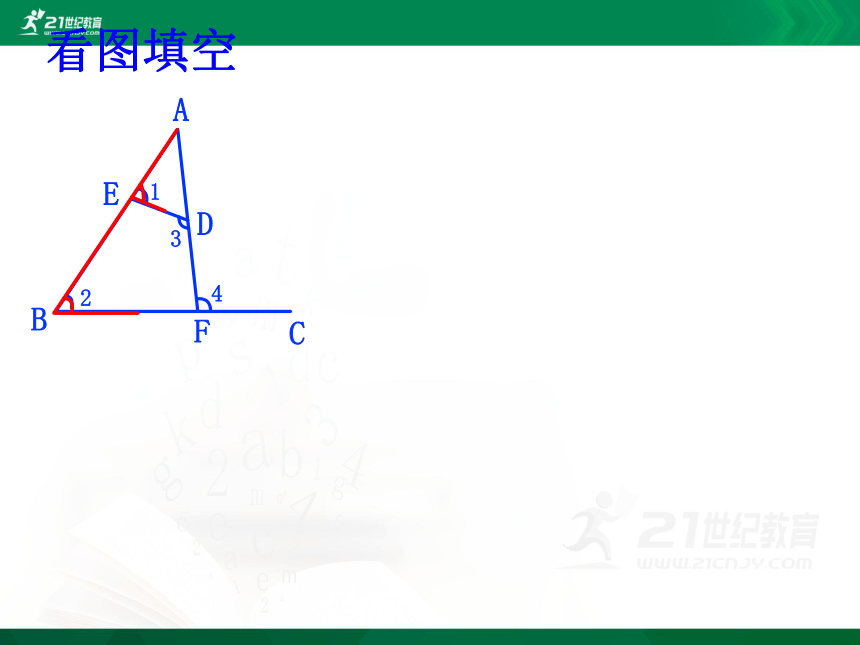
看图填空
×
判断：
1、不相交的两条直线叫做平行线。
2、在同一平面内不相交的两条直线
叫做平行线。
在同一平面内、
注意
平行线体现三点：
不相交、
两条直线。
在同一平面内
不相交
两条直线
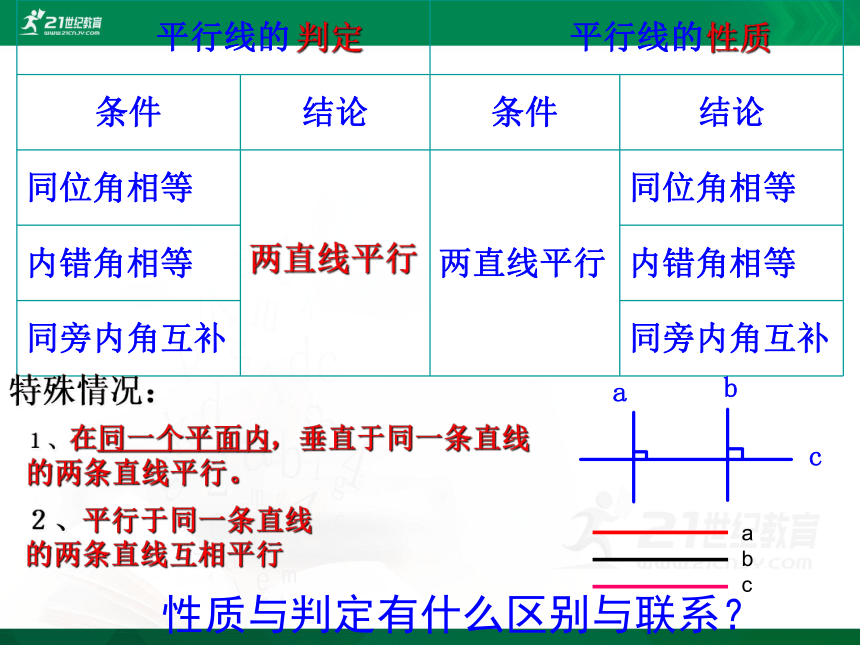
平行线的 平行线的
条件 结论 条件 结论
同位角相等 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
性质与判定有什么区别与联系？
判定
性质
两直线平行
特殊情况：
１、在同一个平面内，垂直于同一条直线
的两条直线平行。
a
b
c
２、平行于同一条直线
的两条直线互相平行
A
B
C
D
E
F
1
2
3
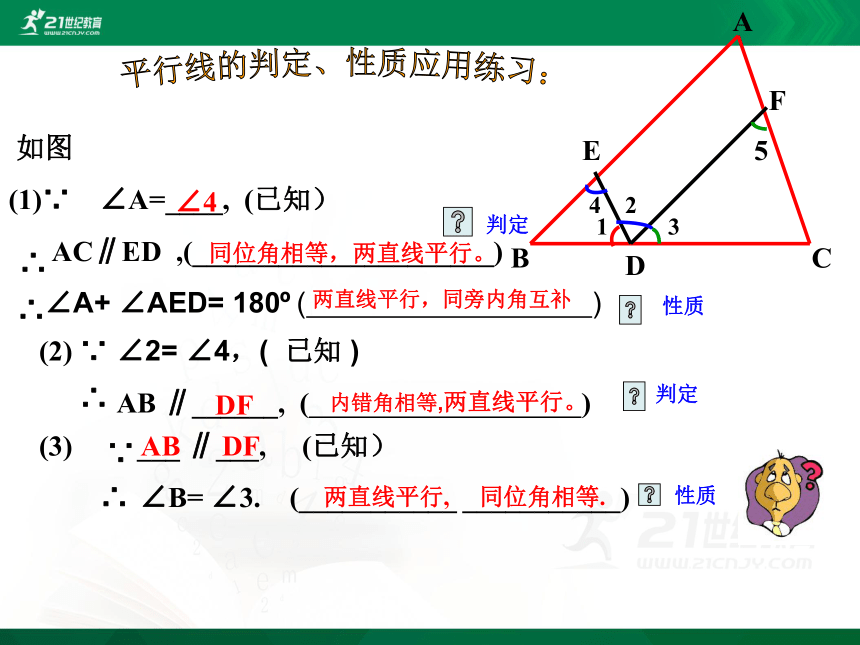
如图
(1)∵　∠A=____, (已知）
AC∥ED ,(_____________________)
∠A+ ∠AED= 180 ( )
(2) ∵ ∠2= ∠4，( 已知 )
AB ∥______, ( )
4
5
(3) ___ ∥___, (已知）
∠B= ∠3. (___________ ___________)
∠4
同位角相等，两直线平行。
DF
内错角相等,两直线平行。
AB
DF
两直线平行, 同位角相等.
判定
判定
性质
∴
∴
∴
∵
两直线平行，同旁内角互补
∴
性质
2、如图, 若∠3=∠4，则 ∥ ；
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD, 则∠ =∠ 。
BC
2
3、如图，∠D=70°，∠C= 110°,∠1=69°，
则∠B= ·
B
A
C
E
D
⌒
1
69°
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
4、如图，已知AB∥CD，补充什么条件，能得AD=BC？
6. 若两条平行线被第三条直线所截，则一组内错角的平分线互相（ ）
A 垂直 B 平行 C 重合 D 相交
5. 两条直线被第三条直线所截，则（ ）
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
7.夹在平行线间的两条线段相等，则两条线段所在的直线的位置关系是（ ）
A 平行 B 相交 C 平行或相交 D不能确定
D
B
D
例1、如图，已知CD⊥AB，GF⊥AB，DE∥BC
说明：∠1＝∠2的理由
∴∠1＝∠2（等量代换）
解∵CD⊥AB，GF⊥AB（已知）
∴CD∥GF（在同一平面内，垂直于同一直线的两条直线平行）
∴∠2＝∠DCB（两直线平行，同位角相等）
∵DE∥BC（已知）
∴∠1＝∠DCB（两直线平行，内错角相等）
变式练1: 如图，BD⊥AC，EF⊥AC，D、F分别为垂足，∠1＝∠2，试说明∠ADG ＝∠C 。
解： ∵ BD⊥AC，EF⊥AC
　　∴ EF∥DB
　　∴ ∠2=∠DBC(两直线平行,同位角相等）
　又∵ ∠1＝∠2
　　∴ ∠１=∠DBC
　　∴ DG∥BC(内错角相等，两直线平行)
　　∴∠ADG=∠C（两直线平行，同位角相等）
变式练2：如图， △ABC中， ∠B＝∠C，AE是外角∠DAC的平分线，那么AE ∥BC ，请完成推理过程。
解∵ ∠DAC是△ABC的一个外角
∴ ∠DAC＝∠B＋∠C
（
　　　　　　　　）
∵ ∠B＝∠C（　　　）
∴ ∠DAC＝2∠B（　　　　　）
∵ AE是∠DAC的平分线（　　）
∴ ∠DAC＝2∠ 　（　　　　　　）
∴ ∠B＝∠ （　　　　　　　　）
∴AE ∥BC　（　　　　　　　　　　）
（已知）
三角形的一个外角等于和它不相
邻的两内角之和
　已知
　　等量代换
　已知
DAE
DAE
　同位角相等，两直线平行
　角平分线的意义
　　等量代换
例2：如图，已知AB∥CD
猜想∠BED,∠B与∠D有什么关系
两平行线间凹凸角的关系问题
A
B
E
D
C
此类题的特征是: 添辅助线使之产生”三线八角”
如图AB∥CD，EF与GH交于点O，
试问∠1与∠2、 ∠3有怎样的等量关系？
A
B
C
D
E
F
G
H
O
1
2
3
解： ∠1与∠2， ∠3的关系是
∠3= ∠1＋ ∠2，理由如下：
过点O做OP ∥AB，由OP ∥AB，
得∠2= ∠4，
P
4
5
∵ AB∥CD ∴OP ∥ CD
∴ ∠ 1= ∠ 5（两直线平行，同位角相等）
而∠3= ∠4＋ ∠5，
∴ ∠3= ∠2＋ ∠1。
练习
α
500
例3：如图，平面镜OA，OB的夹角为50度，若要使一条光线经两个镜面反射后沿与OA平行的方向射出，你能求出入射角α度数吗？
镜面成像问题
此类题的特征是: 入射角=反射角
两块平面镜的夹角应为多少度
如图，两平面镜а、β的夹角为θ，入射光线AO平行于β入射到а上，经两次反射后的反射光线 平行于а，则角θ=_____度
а
β
θ
O
B
A
1
2
3
4
5
练习
例4：如图，m∥n，问图中有那些三角形的面积相等，为什么？
A
B
C
D
O
m
n
∟
∟
解:
△ ABC与△ BCD, △ ABD与△ACD, △ AOB与△ COD面积相等.
∵ △ ABC与△ BCD同底等高
∴ △ ABC与△ BCD面积相等
同理△ ABD与△ ACD面积相等.
∵ S△ ABC - S△ BOC= S△ ABC - S△ BOC
∴ △ AOB与△ COD面积相等.
两平行线间的等积问题
此类题的特征是: 等高
A
B
C
D
E
1、如图,点E是BC的中点,AD∥BC,求△ ABC与
△ CDE的面积之比
2:1
练习
　1、 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
2、如图，CD是△ABC的中线，延长CD至E，使CD=DE.试判断AC与BE是否平行，并说明理由.
A
B
C
D
E
解: AC∥BE理由如下:
CD=DE
∠ADC= ∠BDE
AD=BD
∴ △ ADC ≌ △ BDE(SAS)
∴∠1= ∠2
∴AC ∥ BE
1
2
D
F
C
A
E
B
3、如图所示, 已知AB//CD ,AD//BC, BF平分∠ABC ,DE平分∠ADC,则 DE//FB,请说明理由.
4、 如图，A、F、C、D四点在一直线上，AF ＝ CD，AB//DE，且AB ＝ DE，判断EF和BC是否平行，并说明理由。
5.已知:∠1＝∠2,∠C＝∠D,
说明:DF∥AC
6.已知:∠A＝∠F,∠C＝∠D,
说明:DB∥EC
A
B
C
D
E
F
1
2
7、如图，DE∥BC,你能推出 ∠BAC＋∠B+∠C=180°？还有其它方法吗？
A
B
C
D
E
⌒
⌒
1
2
8、如图，CD平分∠ACB，DE∥AC，且∠1=35°，则∠2是多少度？
A
B
C
D
E
1
2
9、如图，在甲、乙两地之间要修一条笔直的公路，从甲地测得公路的走向是北偏东42 °.甲、乙两地同时开工，若干天后公路准确接通，乙地所修公路的走向是南偏西多少度？为什么？
甲
乙
北
北
42 °
南偏西42 °
10、如图，已知AB∥CD，
试再添上一个条件，
使∠1=∠2成立
11。如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1=∠2，∠3=80°．求∠BCA的度数．
探究思考：
1.如图，AB∥CD，直线FE与两平行线交于点G、H，形成的同位角的角平分线的位置上有什么关系？
A
B
C
D
E
F
G
H
问：
(1)选择其中一对同位角，如：∠AGE与∠CHG看看它们的平分线有什么位置关系？
M
N
(2)其他的同位角也满足吗？你得到什么结论？
(3)思考: 两直线平行,内错角的角平分线满足什么位置关系 同旁内角呢
A
B
C
M
N
2、如图,折线ABC是一片农田中的道路.现需把它改成一条直路,并使道路两边的面积保持不变,道路的一个端点为点A,问应怎样改 要求画出示意图,并说明理由.
O
∴线段AN就是所求的道路改直路线。
折叠三角形纸片ABC，使点A落在BC边上的点F，切折痕DE∥BC。若∠B=50°，求∠BDF的度数，并说明理由。
A
B
C
D
E
F
变一变：将一条两边沿互相平行的纸带按如图折叠，∠1=30度，请求出∠2的度数。
1
2
折叠问题
此类题的特征是:找平行线定角
A
B
C
1
2
3
4
E
F
∠CAB =75°
有一条长方形纸带，按如图所示沿AB折叠时，当∠1=30°求纸带重叠部分中∠CAB的度数。
练习