2022-2023学年浙教版数学七年级下册3.7整式的除法 课件(共26张PPT)
文档属性
| 名称 | 2022-2023学年浙教版数学七年级下册3.7整式的除法 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 700.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-12 00:00:00 | ||
图片预览







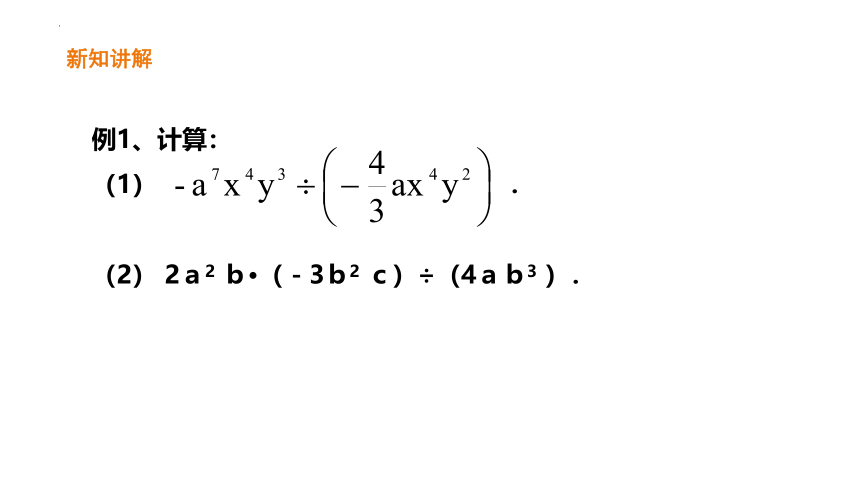
文档简介
(共26张PPT)
3.7 整式的除法
复习导入
亲爱的同学们,上节课我们学习
过同底数幂的除法法则,请同学们回忆一下,并写出来。
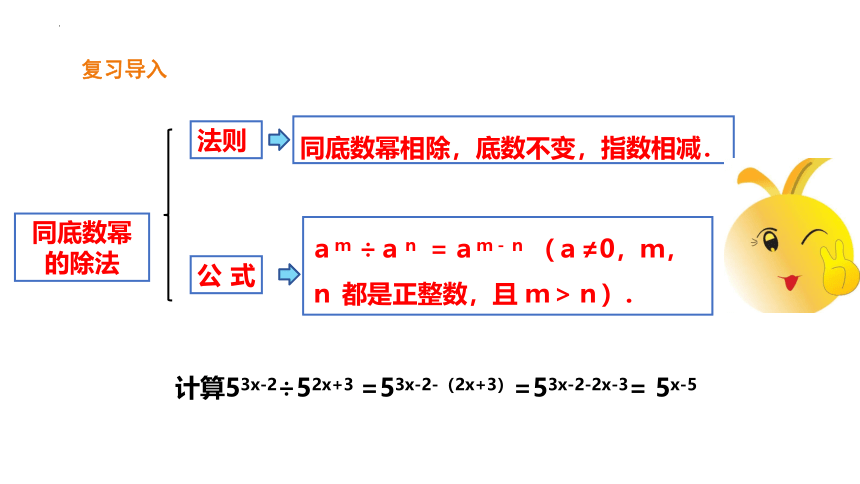
公式
法则
同底数幂的除法
am ÷an =am-n (a≠0,m,n 都是正整数,且 m>n).
同底数幂相除,底数不变,指数相减.
复习导入
计算53x-2÷52x+3
=53x-2-(2x+3)=53x-2-2x-3= 5x-5
新知讲解
本节中,我们将学习整式的除法,包括单项式除以单项式和多项式除以单项式. 我们前面学过的同底数幂相除是单项式相除的特殊情况.
新知讲解
天宫一号目标飞行器与神舟八号飞船第一次对接前,天宫一号在环地球轨道上飞行一周所需的时间为6.0×103秒,行程为4.7×107米.那么天宫一号飞行的速度为每秒多少米?
4.7×107÷ (6.0×103)≈7.8×103
新知讲解
解决上述问题时,你是怎样计算的? 由此你能找到计算(3a8)÷(2a4 )的方法吗? 计算 (6a3b4 )÷(3a2b)呢?
(3a8)÷(2a4 )=
(6a3b4 )÷(3a2b)=2ab3
新知讲解
我们有以下单项式除以单项式的法则:(14a3b2x)÷(4ab2 )
单项式相除,把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
新知讲解
一般地,两个单项式相除,可以转化为系数与系数相除以及同底数幂相除.
新知讲解
例1、计算:
(1) .
(2) 2a2 b·(-3b2 c)÷(4ab3 ).
新知讲解
解:(1)
新知讲解
(2) 2a2 b·(-3b2 c)÷(4ab3 )
新知讲解
做一做
先填空,再用适当的方法验证计算的正确性.
(1)(625+125+50)÷25
=( )÷( )+( )÷( )+( )÷( )
=________.
(2)(4a+6)÷2=( )÷2+( )÷2= ________ .
625 25 125 25 50 25
32
4a
6
2a+3
新知讲解
做一做
(3)(2a2 -a)÷(-2a)
=( )÷(-2a)+( )÷(-2a)= ________.
从上述第(2),(3)题的计算中,你能归纳出多项式除以单项式的运算方法吗?
2a2
-a
-a+0.5
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)
新知讲解
我们有以下多项式除以单项式的法则:
新知讲解
例2、计算:
(1)(14a3 -7a2)÷(7a).
(2)(15x3y5 -10x4y4 -20x3y2 )÷(-5x3y2 ).
新知讲解
解 (1)(14a3-7a2)÷(7a)
=(14a3)÷(7a)+(-7a2 )÷(7a)
=2a2-a.
新知讲解
(2)(15x3 y5 -10x4 y4 -20x3 y2 )÷(-5x3 y2 )
=(15x3y5 )÷(-5x3 y2)+(-10x4 y4 )÷(-5x3 y2)
+(-20x3 y2 )÷(-5x3 y2 )
=-3y3 +2xy2 +4.
课堂练习
1、计算:
(x-2)(x+6)-(6x4-4x3-2x2)÷(-2x2)
解:原式=x2+4x-12-(-3x2+2x+1)
=x2+4x-12+3x2-2x-1
=4x2+2x-13.
课堂练习
2、计算:[(m+n)(m-n)+(m-n) 2-4m(m-n)]÷2m.
解:[(m+n)(m-n)+(m-n)2-4m(m-n)]÷2m
=(m2-n2+m2-2mn+n2-4m2+4mn)÷2m
=(-2m2+2mn)÷2m
课堂练习
3、已知某长方形面积为4a2-6ab+2a,它的一边长为2a,求这个长方形的周长.
解:长方形的另一边长为:
(4a2-6ab+2a)÷(2a)=2a-3b+1,
所以长方形的周长为:
2(2a-3b+1+2a)=8a-6b+2.
观察下列各式:
(x-1)÷(x-1)=1;
(x2-1)÷(x-1)=x+1;
(x3-1)÷(x-1)=x2+x+1;
(x4-1)÷(x-1)=x3+x2+x+1;……
(x8-1)÷(x-1)=x7+x6+x5+...+x+1;
中考链接
(1)根据上面各式的规律可得
(xn-1)÷(x-1)=_______________.
(2)利用(1)的结论求22019+22018+...+2+1的值;
(3)若1+x+x2+...+x2018=0且x-1≠0,求x2019的值。
解:(1)
∵ (x-1)÷(x-1)=1;
(x2-1)÷(x-1)=x+1;
(x3-1)÷(x-1)=x2+x+1;
(x4-1)÷(x-1)=x3+x2+x+1;……
∴ (xn-1)÷(x-1)=xn-1+xn-2+ +1
中考链接
(2)22019+22018+...+2+1
=(22020-1)÷(2-1)
=22020-1;
(3)∵1+x+x2+...+x2018=(x2019-1)÷(x-1)=0
∵x-1≠0
∴x2019-1=0
∴x2019=1.
课堂总结
多项式除以单项式
两个单项式相除
整式
的除法
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
(a+b+c)÷m
=a÷m+b÷m+c÷m(m≠0)
单项式相除,把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
板书设计
3.7 整式的除法
一、两个单项式相除
二、多项式除以单项式
(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)
3.7 整式的除法
复习导入
亲爱的同学们,上节课我们学习
过同底数幂的除法法则,请同学们回忆一下,并写出来。
公式
法则
同底数幂的除法
am ÷an =am-n (a≠0,m,n 都是正整数,且 m>n).
同底数幂相除,底数不变,指数相减.
复习导入
计算53x-2÷52x+3
=53x-2-(2x+3)=53x-2-2x-3= 5x-5
新知讲解
本节中,我们将学习整式的除法,包括单项式除以单项式和多项式除以单项式. 我们前面学过的同底数幂相除是单项式相除的特殊情况.
新知讲解
天宫一号目标飞行器与神舟八号飞船第一次对接前,天宫一号在环地球轨道上飞行一周所需的时间为6.0×103秒,行程为4.7×107米.那么天宫一号飞行的速度为每秒多少米?
4.7×107÷ (6.0×103)≈7.8×103
新知讲解
解决上述问题时,你是怎样计算的? 由此你能找到计算(3a8)÷(2a4 )的方法吗? 计算 (6a3b4 )÷(3a2b)呢?
(3a8)÷(2a4 )=
(6a3b4 )÷(3a2b)=2ab3
新知讲解
我们有以下单项式除以单项式的法则:(14a3b2x)÷(4ab2 )
单项式相除,把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
新知讲解
一般地,两个单项式相除,可以转化为系数与系数相除以及同底数幂相除.
新知讲解
例1、计算:
(1) .
(2) 2a2 b·(-3b2 c)÷(4ab3 ).
新知讲解
解:(1)
新知讲解
(2) 2a2 b·(-3b2 c)÷(4ab3 )
新知讲解
做一做
先填空,再用适当的方法验证计算的正确性.
(1)(625+125+50)÷25
=( )÷( )+( )÷( )+( )÷( )
=________.
(2)(4a+6)÷2=( )÷2+( )÷2= ________ .
625 25 125 25 50 25
32
4a
6
2a+3
新知讲解
做一做
(3)(2a2 -a)÷(-2a)
=( )÷(-2a)+( )÷(-2a)= ________.
从上述第(2),(3)题的计算中,你能归纳出多项式除以单项式的运算方法吗?
2a2
-a
-a+0.5
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)
新知讲解
我们有以下多项式除以单项式的法则:
新知讲解
例2、计算:
(1)(14a3 -7a2)÷(7a).
(2)(15x3y5 -10x4y4 -20x3y2 )÷(-5x3y2 ).
新知讲解
解 (1)(14a3-7a2)÷(7a)
=(14a3)÷(7a)+(-7a2 )÷(7a)
=2a2-a.
新知讲解
(2)(15x3 y5 -10x4 y4 -20x3 y2 )÷(-5x3 y2 )
=(15x3y5 )÷(-5x3 y2)+(-10x4 y4 )÷(-5x3 y2)
+(-20x3 y2 )÷(-5x3 y2 )
=-3y3 +2xy2 +4.
课堂练习
1、计算:
(x-2)(x+6)-(6x4-4x3-2x2)÷(-2x2)
解:原式=x2+4x-12-(-3x2+2x+1)
=x2+4x-12+3x2-2x-1
=4x2+2x-13.
课堂练习
2、计算:[(m+n)(m-n)+(m-n) 2-4m(m-n)]÷2m.
解:[(m+n)(m-n)+(m-n)2-4m(m-n)]÷2m
=(m2-n2+m2-2mn+n2-4m2+4mn)÷2m
=(-2m2+2mn)÷2m
课堂练习
3、已知某长方形面积为4a2-6ab+2a,它的一边长为2a,求这个长方形的周长.
解:长方形的另一边长为:
(4a2-6ab+2a)÷(2a)=2a-3b+1,
所以长方形的周长为:
2(2a-3b+1+2a)=8a-6b+2.
观察下列各式:
(x-1)÷(x-1)=1;
(x2-1)÷(x-1)=x+1;
(x3-1)÷(x-1)=x2+x+1;
(x4-1)÷(x-1)=x3+x2+x+1;……
(x8-1)÷(x-1)=x7+x6+x5+...+x+1;
中考链接
(1)根据上面各式的规律可得
(xn-1)÷(x-1)=_______________.
(2)利用(1)的结论求22019+22018+...+2+1的值;
(3)若1+x+x2+...+x2018=0且x-1≠0,求x2019的值。
解:(1)
∵ (x-1)÷(x-1)=1;
(x2-1)÷(x-1)=x+1;
(x3-1)÷(x-1)=x2+x+1;
(x4-1)÷(x-1)=x3+x2+x+1;……
∴ (xn-1)÷(x-1)=xn-1+xn-2+ +1
中考链接
(2)22019+22018+...+2+1
=(22020-1)÷(2-1)
=22020-1;
(3)∵1+x+x2+...+x2018=(x2019-1)÷(x-1)=0
∵x-1≠0
∴x2019-1=0
∴x2019=1.
课堂总结
多项式除以单项式
两个单项式相除
整式
的除法
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
(a+b+c)÷m
=a÷m+b÷m+c÷m(m≠0)
单项式相除,把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
板书设计
3.7 整式的除法
一、两个单项式相除
二、多项式除以单项式
(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
