1.2 同位角、内错角、同旁内角 同步练习(含答案)
文档属性
| 名称 | 1.2 同位角、内错角、同旁内角 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 19:14:37 | ||
图片预览




文档简介
1.2 同位角、内错角、同旁内角
1.如图,∠1的同旁内角是( )
A.∠2 B.∠3 C.∠4 D.∠5
第1题图 第2题图 第4题图
2.如图,∠B的同位角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.【2022·杭州萧山区调研】下列图形中,∠1与∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个
4.【2022·杭州拱墅区期末】如图,下列说法正确的是( )
A.∠1和∠2是内错角 B.∠1和∠3是内错角
C.∠1和∠3是同位角 D.∠2和∠3是同旁内角
5.如图,∠1和∠2是内错角,可看成是直线( )
A.AB,BC被CE所截构成的 B.DC,EC被AB所截构成的
C.EC,EB被BC所截构成的 D.DC,EB被EC所截构成的
第5题图 第6题图 第7题图
6.如图,如果∠α=135°,那么∠β的同位角等于________°,∠β的内错角等于________°,∠β的同旁内角等于________°.
7.如图,两条直线被第三条直线所截,∠1是∠2的内错角,∠2是∠3的同旁内角. 若3∠1=∠3,∠2∶∠3=1∶2,则∠1=____,∠2=____,∠3=____.
8.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是________.(填序号)
9.【2022·杭州之江实验中学期中】如图,下列说法中,错误的是( )
A.∠3与∠B是同旁内角 B.∠A与∠1是同位角
C.∠2与∠3是内错角 D.∠1与∠B是同位角
第9题图 第10题图 第11题图
10.如图,与∠B是同旁内角的角有( )
A.1个 B.2个 C.3个 D.4个
11.如图,下列说法正确的是( )
A.∠1和∠2是内错角 B.∠1和∠5是同位角 C.∠1和∠2是同旁内角 D.∠1和∠4是内错角
12.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( )
13.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ,内错角是 ,同旁内角是 .
第13题图 第14题图 第15题图
14.如图,∠B与∠1是两条直线 和 被直线 所截得到的一对 角;∠2和∠4是两条直线 和 被直线 所截得到的一对 角;∠ACB和∠3是两条直线 和 被第三条直线 所截得到的一对 角.
15.如图所示,同位角有a对,内错角有b对,同旁内角有c对,则的值是 .
16.根据图形填空:
(1)直线ED,BC被直线AB所截,则∠1和 是同位角;
(2)直线ED,BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠5是直线AB,AF被直线 所截构成的同旁内角;
(4)∠2和∠4是直线AB, 被直线BC所截构成的 角.
17.两条直线被第三条直线所截,得到∠1,∠2,∠3,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
18.已知:
如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始角∠1跳到终点角∠3,可以写出其中两种不同的路径,
路径1:∠1∠9∠3.
路径2:∠1∠12∠6∠10∠3.
试一试:
(1)从起始角∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8
19.探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
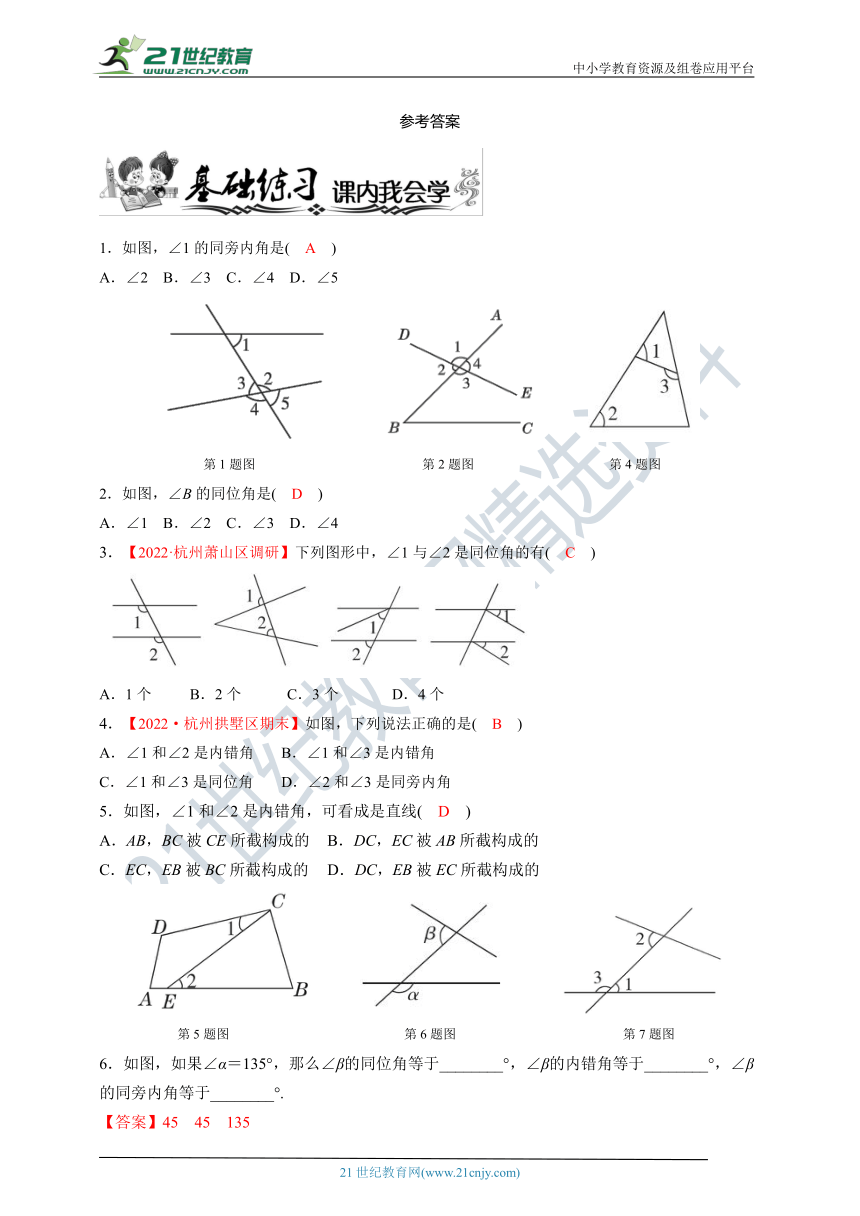
1.如图,∠1的同旁内角是( A )
A.∠2 B.∠3 C.∠4 D.∠5
第1题图 第2题图 第4题图
2.如图,∠B的同位角是( D )
A.∠1 B.∠2 C.∠3 D.∠4
3.【2022·杭州萧山区调研】下列图形中,∠1与∠2是同位角的有( C )
A.1个 B.2个 C.3个 D.4个
4.【2022·杭州拱墅区期末】如图,下列说法正确的是( B )
A.∠1和∠2是内错角 B.∠1和∠3是内错角
C.∠1和∠3是同位角 D.∠2和∠3是同旁内角
5.如图,∠1和∠2是内错角,可看成是直线( D )
A.AB,BC被CE所截构成的 B.DC,EC被AB所截构成的
C.EC,EB被BC所截构成的 D.DC,EB被EC所截构成的
第5题图 第6题图 第7题图
6.如图,如果∠α=135°,那么∠β的同位角等于________°,∠β的内错角等于________°,∠β的同旁内角等于________°.
【答案】45 45 135
7.如图,两条直线被第三条直线所截,∠1是∠2的内错角,∠2是∠3的同旁内角. 若3∠1=∠3,∠2∶∠3=1∶2,则∠1=____,∠2=____,∠3=____.
【答案】45° 67.5° 135°
8.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是________.(填序号)
【答案】①②③
9.【2022·杭州之江实验中学期中】如图,下列说法中,错误的是( D )
A.∠3与∠B是同旁内角 B.∠A与∠1是同位角
C.∠2与∠3是内错角 D.∠1与∠B是同位角
第9题图 第10题图 第11题图
10.如图,与∠B是同旁内角的角有( C )
A.1个 B.2个 C.3个 D.4个
11.如图,下列说法正确的是( C )
A.∠1和∠2是内错角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠1和∠4是内错角
12.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( C )
13.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ∠1与∠B,∠4与∠B ,内错角是 ∠2与∠5,∠3与∠4 ,同旁内角是 ∠B和∠3,∠B和∠5,∠2与∠4,∠3与∠5 .
第13题图 第14题图 第15题图
14.如图,∠B与∠1是两条直线 DE 和 BC 被直线 AB 所截得到的一对 同位 角;∠2和∠4是两条直线 DE 和 BC 被直线 DC 所截得到的一对 内错 角;∠ACB和∠3是两条直线 DE 和 BC 被第三条直线 AC 所截得到的一对 同旁内 角.
15.如图所示,同位角有a对,内错角有b对,同旁内角有c对,则的值是 .
【答案】2
16.根据图形填空:
(1)直线ED,BC被直线AB所截,则∠1和 是同位角;
(2)直线ED,BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠5是直线AB,AF被直线 所截构成的同旁内角;
(4)∠2和∠4是直线AB, 被直线BC所截构成的 角.
【答案】∠2 ∠4 ED AF 同位
17.两条直线被第三条直线所截,得到∠1,∠2,∠3,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
解:如图(画图不唯一,符合题意即可).
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
解:设∠3=x,则∠2=2x,∠1=4x.
∵∠1+∠3=180°,
∴5x=180°,解得x=36°.
∴∠1=144°,∠2=72°,∠3=36°.
18.已知:
如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始角∠1跳到终点角∠3,可以写出其中两种不同的路径,
路径1:∠1∠9∠3.
路径2:∠1∠12∠6∠10∠3.
试一试:
(1)从起始角∠1跳到终点角∠8;
解:路径:∠1 ∠12 ∠8(答案不唯一).
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8
解:从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8.
路径:∠1∠10∠5∠8.
19.探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
【答案】4 2 2
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
【答案】12 6 6
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
【答案】2n(n-1) n(n-1) n(n-1)
【思路点拨】(1)要求同位角、内错角和同旁内角的对数,图①中的图形是“三线八角”的基本图形,所以容易得出;
(2)把图②中的图形进行拆分得3个“三线八角”的基本图形,即可求出;
(3)当有n条水平直线时,可以拆分成个“三线八角”的基本图形,从而得出规律.
【点规律】本题中的规律也可以这样总结:当n条水平直线被一条竖直直线所截时,内错角和同旁内角各有n(n-1)对,而同位角的对数是内错角的对数的2倍,因此有2n(n-1)对
1.如图,∠1的同旁内角是( )
A.∠2 B.∠3 C.∠4 D.∠5
第1题图 第2题图 第4题图
2.如图,∠B的同位角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.【2022·杭州萧山区调研】下列图形中,∠1与∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个
4.【2022·杭州拱墅区期末】如图,下列说法正确的是( )
A.∠1和∠2是内错角 B.∠1和∠3是内错角
C.∠1和∠3是同位角 D.∠2和∠3是同旁内角
5.如图,∠1和∠2是内错角,可看成是直线( )
A.AB,BC被CE所截构成的 B.DC,EC被AB所截构成的
C.EC,EB被BC所截构成的 D.DC,EB被EC所截构成的
第5题图 第6题图 第7题图
6.如图,如果∠α=135°,那么∠β的同位角等于________°,∠β的内错角等于________°,∠β的同旁内角等于________°.
7.如图,两条直线被第三条直线所截,∠1是∠2的内错角,∠2是∠3的同旁内角. 若3∠1=∠3,∠2∶∠3=1∶2,则∠1=____,∠2=____,∠3=____.
8.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是________.(填序号)
9.【2022·杭州之江实验中学期中】如图,下列说法中,错误的是( )
A.∠3与∠B是同旁内角 B.∠A与∠1是同位角
C.∠2与∠3是内错角 D.∠1与∠B是同位角
第9题图 第10题图 第11题图
10.如图,与∠B是同旁内角的角有( )
A.1个 B.2个 C.3个 D.4个
11.如图,下列说法正确的是( )
A.∠1和∠2是内错角 B.∠1和∠5是同位角 C.∠1和∠2是同旁内角 D.∠1和∠4是内错角
12.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( )
13.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ,内错角是 ,同旁内角是 .
第13题图 第14题图 第15题图
14.如图,∠B与∠1是两条直线 和 被直线 所截得到的一对 角;∠2和∠4是两条直线 和 被直线 所截得到的一对 角;∠ACB和∠3是两条直线 和 被第三条直线 所截得到的一对 角.
15.如图所示,同位角有a对,内错角有b对,同旁内角有c对,则的值是 .
16.根据图形填空:
(1)直线ED,BC被直线AB所截,则∠1和 是同位角;
(2)直线ED,BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠5是直线AB,AF被直线 所截构成的同旁内角;
(4)∠2和∠4是直线AB, 被直线BC所截构成的 角.
17.两条直线被第三条直线所截,得到∠1,∠2,∠3,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
18.已知:
如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始角∠1跳到终点角∠3,可以写出其中两种不同的路径,
路径1:∠1∠9∠3.
路径2:∠1∠12∠6∠10∠3.
试一试:
(1)从起始角∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8
19.探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,∠1的同旁内角是( A )
A.∠2 B.∠3 C.∠4 D.∠5
第1题图 第2题图 第4题图
2.如图,∠B的同位角是( D )
A.∠1 B.∠2 C.∠3 D.∠4
3.【2022·杭州萧山区调研】下列图形中,∠1与∠2是同位角的有( C )
A.1个 B.2个 C.3个 D.4个
4.【2022·杭州拱墅区期末】如图,下列说法正确的是( B )
A.∠1和∠2是内错角 B.∠1和∠3是内错角
C.∠1和∠3是同位角 D.∠2和∠3是同旁内角
5.如图,∠1和∠2是内错角,可看成是直线( D )
A.AB,BC被CE所截构成的 B.DC,EC被AB所截构成的
C.EC,EB被BC所截构成的 D.DC,EB被EC所截构成的
第5题图 第6题图 第7题图
6.如图,如果∠α=135°,那么∠β的同位角等于________°,∠β的内错角等于________°,∠β的同旁内角等于________°.
【答案】45 45 135
7.如图,两条直线被第三条直线所截,∠1是∠2的内错角,∠2是∠3的同旁内角. 若3∠1=∠3,∠2∶∠3=1∶2,则∠1=____,∠2=____,∠3=____.
【答案】45° 67.5° 135°
8.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是________.(填序号)
【答案】①②③
9.【2022·杭州之江实验中学期中】如图,下列说法中,错误的是( D )
A.∠3与∠B是同旁内角 B.∠A与∠1是同位角
C.∠2与∠3是内错角 D.∠1与∠B是同位角
第9题图 第10题图 第11题图
10.如图,与∠B是同旁内角的角有( C )
A.1个 B.2个 C.3个 D.4个
11.如图,下列说法正确的是( C )
A.∠1和∠2是内错角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠1和∠4是内错角
12.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( C )
13.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ∠1与∠B,∠4与∠B ,内错角是 ∠2与∠5,∠3与∠4 ,同旁内角是 ∠B和∠3,∠B和∠5,∠2与∠4,∠3与∠5 .
第13题图 第14题图 第15题图
14.如图,∠B与∠1是两条直线 DE 和 BC 被直线 AB 所截得到的一对 同位 角;∠2和∠4是两条直线 DE 和 BC 被直线 DC 所截得到的一对 内错 角;∠ACB和∠3是两条直线 DE 和 BC 被第三条直线 AC 所截得到的一对 同旁内 角.
15.如图所示,同位角有a对,内错角有b对,同旁内角有c对,则的值是 .
【答案】2
16.根据图形填空:
(1)直线ED,BC被直线AB所截,则∠1和 是同位角;
(2)直线ED,BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠5是直线AB,AF被直线 所截构成的同旁内角;
(4)∠2和∠4是直线AB, 被直线BC所截构成的 角.
【答案】∠2 ∠4 ED AF 同位
17.两条直线被第三条直线所截,得到∠1,∠2,∠3,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
解:如图(画图不唯一,符合题意即可).
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
解:设∠3=x,则∠2=2x,∠1=4x.
∵∠1+∠3=180°,
∴5x=180°,解得x=36°.
∴∠1=144°,∠2=72°,∠3=36°.
18.已知:
如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始角∠1跳到终点角∠3,可以写出其中两种不同的路径,
路径1:∠1∠9∠3.
路径2:∠1∠12∠6∠10∠3.
试一试:
(1)从起始角∠1跳到终点角∠8;
解:路径:∠1 ∠12 ∠8(答案不唯一).
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点角∠8
解:从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点角∠8.
路径:∠1∠10∠5∠8.
19.探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
【答案】4 2 2
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
【答案】12 6 6
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
【答案】2n(n-1) n(n-1) n(n-1)
【思路点拨】(1)要求同位角、内错角和同旁内角的对数,图①中的图形是“三线八角”的基本图形,所以容易得出;
(2)把图②中的图形进行拆分得3个“三线八角”的基本图形,即可求出;
(3)当有n条水平直线时,可以拆分成个“三线八角”的基本图形,从而得出规律.
【点规律】本题中的规律也可以这样总结:当n条水平直线被一条竖直直线所截时,内错角和同旁内角各有n(n-1)对,而同位角的对数是内错角的对数的2倍,因此有2n(n-1)对
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
