1.3.1 利用同位角判定两直线平行 同步练习(含答案)
文档属性
| 名称 | 1.3.1 利用同位角判定两直线平行 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 19:13:02 | ||
图片预览




文档简介
1.3 平行线的判定
第1课时 利用同位角判定两直线平行
1.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
第1题图 第2题图 第3题图
2.【2022·宁波市镇海区蛟川书院期末】如图,点E在AC的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠1=∠2 B.∠A=∠DCE C.∠D=∠DCE D.∠D+∠ACD=180°
3.对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠2+∠3=∠4 B.∠2=∠4
C.∠1=∠4 D.∠3=∠4
4.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD C.CA平分∠BCD D.AC平分∠BAD
第4题图 第5题图 第7题图
5.如图,已知直线AB,CD被直线EF所截,∠AEF=∠CFH,∠1=∠2,则图中所有的平行线有( )
A.AB∥CD B.PE∥QF
C.AB∥CD和PE∥QF D.PE∥CD
6.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列选项成立的是( )
A.a⊥c B.b⊥d C.a⊥d D.以上都不对
7.如图,由图中的数据,可知平行的直线是____________.
8.已知某品牌遮阳伞的剖面示意图如图所示,若AG同时平分∠BAC与∠EDF,且∠BAC=∠EDF,判断AC,DF是否平行,并说明理由.
9.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短在同一平面内,垂直于同一条
直线的两条直线互相平行
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
第9题图 第11题图 第12题图
10.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次左拐50°,第二次左拐130°
11.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,要使直线b与直线c平行,可将直线b绕点A逆时针旋转( )
A.15° B.30° C.45° D.60°
12.小明把一副三角板按如图所示的方式摆放,其中BC,DF在同一条直线上,可以得到______∥______,依据是_____________________________________________.
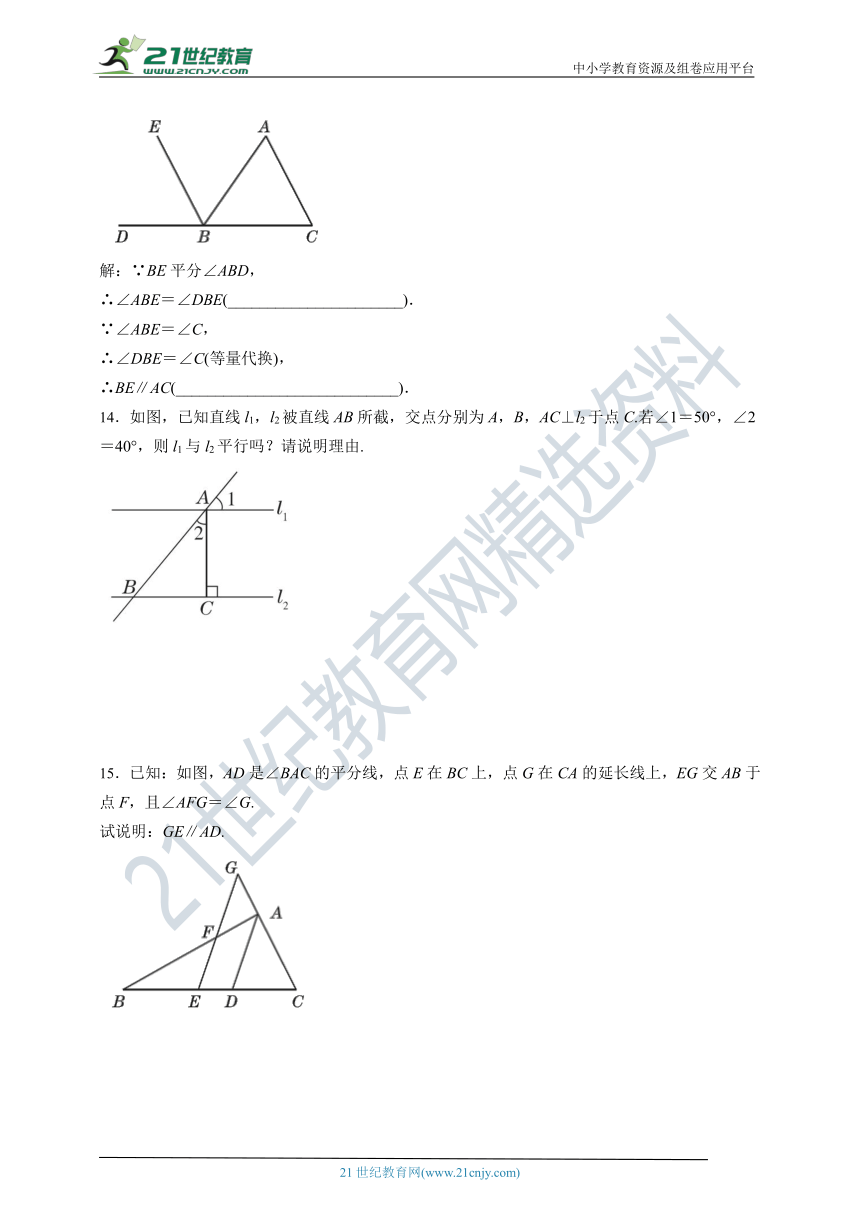
13.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
解:∵BE平分∠ABD,
∴∠ABE=∠DBE(______________________).
∵∠ABE=∠C,
∴∠DBE=∠C(等量代换),
∴BE∥AC(____________________________).
14.如图,已知直线l1,l2被直线AB所截,交点分别为A,B,AC⊥l2于点C.若∠1=50°,∠2=40°,则l1与l2平行吗?请说明理由.
15.已知:如图,AD是∠BAC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.
试说明:GE∥AD.
16.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)请说明AB∥CD.
(2)试问BM与DN是否平行?为什么?
17.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.
问:CE与DF的位置关系怎样?试说明理由.
18.(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由;
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
19.如图,EF⊥BC于点F,DE⊥AB,DE交BC于点D.若∠B=∠ADE,则AD与EF平行吗?请说明理由.
20.如图,MN⊥AB于点D,∠ABC=120°,∠BCF=30°,试判断直线MN与EF的位置关系,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,∠1=120°,要使a∥b,则∠2的大小是( D )
A.60° B.80° C.100° D.120°
第1题图 第2题图 第3题图
2.【2022·宁波市镇海区蛟川书院期末】如图,点E在AC的延长线上,下列条件中,能判定AB∥CD的是( B )
A.∠1=∠2 B.∠A=∠DCE C.∠D=∠DCE D.∠D+∠ACD=180°
3.对于图中标记的各角,下列条件能够推理得到a∥b的是( A )
A.∠2+∠3=∠4 B.∠2=∠4
C.∠1=∠4 D.∠3=∠4
4.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( B )
A.AD∥BC B.AB∥CD C.CA平分∠BCD D.AC平分∠BAD
第4题图 第5题图 第7题图
5.如图,已知直线AB,CD被直线EF所截,∠AEF=∠CFH,∠1=∠2,则图中所有的平行线有( C )
A.AB∥CD B.PE∥QF
C.AB∥CD和PE∥QF D.PE∥CD
6.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列选项成立的是( C )
A.a⊥c B.b⊥d C.a⊥d D.以上都不对
【解析】∵a⊥b,b⊥c,∴a∥c.
∵b⊥c,c⊥d,∴b∥d.
∵b∥d,a⊥b,
∴a⊥d.故C正确.
7.如图,由图中的数据,可知平行的直线是____________.
【答案】EF和GH
8.已知某品牌遮阳伞的剖面示意图如图所示,若AG同时平分∠BAC与∠EDF,且∠BAC=∠EDF,判断AC,DF是否平行,并说明理由.
解:AC∥DF.理由如下:
∵AG平分∠BAC,∴∠GAC=∠BAC.
∵AG平分∠EDF,∴∠GDF=∠EDF.
∵∠BAC=∠EDF,
∴∠GAC=∠GDF.∴AC∥DF.
9.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( B )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短在同一平面内,垂直于同一条
直线的两条直线互相平行
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
第9题图 第11题图 第12题图
10.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( A )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次左拐50°,第二次左拐130°
11.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,要使直线b与直线c平行,可将直线b绕点A逆时针旋转( A )
A.15° B.30° C.45° D.60°
12.小明把一副三角板按如图所示的方式摆放,其中BC,DF在同一条直线上,可以得到______∥______,依据是_____________________________________________.
【答案】AC DE 在同一平面内,垂直于同一条直线的两条直线互相平行
13.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
解:∵BE平分∠ABD,
∴∠ABE=∠DBE(______________________).
∵∠ABE=∠C,
∴∠DBE=∠C(等量代换),
∴BE∥AC(____________________________).
【答案】角平分线的定义
同位角相等,两直线平行
14.如图,已知直线l1,l2被直线AB所截,交点分别为A,B,AC⊥l2于点C.若∠1=50°,∠2=40°,则l1与l2平行吗?请说明理由.
解:l1∥l2.理由如下:如图.
∵∠1=50°,∠2=40°,
∴∠3=180°-∠1-∠2=90°,
∴AC⊥l1. 又∵AC⊥l2,∴l1∥l2.
15.已知:如图,AD是∠BAC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.
试说明:GE∥AD.
解:∵∠FAG+∠BAC=180°,∠FAG+∠G+∠AFG=180°,
∴∠BAC=∠G+∠AFG
又∵∠AFG=∠G,
∴∠BAC=2∠G.
∵AD是∠BAC的平分线,
∴∠BAC=2∠DAC,
∴2∠G=2∠DAC(等量代换).
∴∠G=∠DAC.
∴GE∥AD (同位角相等,两直线平行).
16.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)请说明AB∥CD.
解:∵AB⊥EF,CD⊥EF,∴AB∥CD.
(2)试问BM与DN是否平行?为什么?
解:BM∥DN.理由如下:
∵AB⊥EF,CD⊥EF,
∴∠ABE=∠CDE=90°.
∵∠1=∠2,∴∠ABE-∠1=∠CDE-∠2,即∠MBE=∠NDE.
∴BM∥DN.
17.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.
问:CE与DF的位置关系怎样?试说明理由.
解:CE∥DF.理由如下:
∵BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ABC,∠BCE=∠ACB.
∵∠ABC=∠ACB,∴∠DBC=∠BCE.
∵∠DBF=∠F,∴∠BCE=∠F.
∴CE∥DF.
18.(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由;
解:AB∥CD.理由如下.
∵AB⊥EF,CD⊥EF,∴AB∥CD.
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
解:如图,延长NO′交AB于点P.
∵OM平分∠EOB,O′N平分∠CO′F,
∴∠EOM=∠FO′N=45°.
∵∠FO′N=∠EO′P,
∴∠EOM=∠EO′P=45°.
∴OM∥O′N.
19.如图,EF⊥BC于点F,DE⊥AB,DE交BC于点D.若∠B=∠ADE,则AD与EF平行吗?请说明理由.
解:AD∥EF.理由如下:
∵EF⊥BC,∴∠EFB=90°.
∴∠B+∠BEF=90°.
∵DE⊥AB,∴∠DEA=90°.
∴∠ADE+∠DAB=90°.
∵∠B=∠ADE,∴∠BEF=∠DAB.∴AD∥EF.
20.如图,MN⊥AB于点D,∠ABC=120°,∠BCF=30°,试判断直线MN与EF的位置关系,并说明理由.
解:MN∥EF. 理由如下:延长AB交EF于点G.
∵∠ABC=120°,
∴∠GBC=180°-∠ABC=60°.
∵∠GBC+∠BGC+∠BCF=180°,∠BCF=30°,
∴∠BGC=180°-∠GBC-∠BCF=90°,∴AG⊥EF.
又∵AB⊥MN,∴MN∥EF.
第1课时 利用同位角判定两直线平行
1.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
第1题图 第2题图 第3题图
2.【2022·宁波市镇海区蛟川书院期末】如图,点E在AC的延长线上,下列条件中,能判定AB∥CD的是( )
A.∠1=∠2 B.∠A=∠DCE C.∠D=∠DCE D.∠D+∠ACD=180°
3.对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠2+∠3=∠4 B.∠2=∠4
C.∠1=∠4 D.∠3=∠4
4.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD C.CA平分∠BCD D.AC平分∠BAD
第4题图 第5题图 第7题图
5.如图,已知直线AB,CD被直线EF所截,∠AEF=∠CFH,∠1=∠2,则图中所有的平行线有( )
A.AB∥CD B.PE∥QF
C.AB∥CD和PE∥QF D.PE∥CD
6.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列选项成立的是( )
A.a⊥c B.b⊥d C.a⊥d D.以上都不对
7.如图,由图中的数据,可知平行的直线是____________.
8.已知某品牌遮阳伞的剖面示意图如图所示,若AG同时平分∠BAC与∠EDF,且∠BAC=∠EDF,判断AC,DF是否平行,并说明理由.
9.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短在同一平面内,垂直于同一条
直线的两条直线互相平行
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
第9题图 第11题图 第12题图
10.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次左拐50°,第二次左拐130°
11.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,要使直线b与直线c平行,可将直线b绕点A逆时针旋转( )
A.15° B.30° C.45° D.60°
12.小明把一副三角板按如图所示的方式摆放,其中BC,DF在同一条直线上,可以得到______∥______,依据是_____________________________________________.
13.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
解:∵BE平分∠ABD,
∴∠ABE=∠DBE(______________________).
∵∠ABE=∠C,
∴∠DBE=∠C(等量代换),
∴BE∥AC(____________________________).
14.如图,已知直线l1,l2被直线AB所截,交点分别为A,B,AC⊥l2于点C.若∠1=50°,∠2=40°,则l1与l2平行吗?请说明理由.
15.已知:如图,AD是∠BAC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.
试说明:GE∥AD.
16.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)请说明AB∥CD.
(2)试问BM与DN是否平行?为什么?
17.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.
问:CE与DF的位置关系怎样?试说明理由.
18.(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由;
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
19.如图,EF⊥BC于点F,DE⊥AB,DE交BC于点D.若∠B=∠ADE,则AD与EF平行吗?请说明理由.
20.如图,MN⊥AB于点D,∠ABC=120°,∠BCF=30°,试判断直线MN与EF的位置关系,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,∠1=120°,要使a∥b,则∠2的大小是( D )
A.60° B.80° C.100° D.120°
第1题图 第2题图 第3题图
2.【2022·宁波市镇海区蛟川书院期末】如图,点E在AC的延长线上,下列条件中,能判定AB∥CD的是( B )
A.∠1=∠2 B.∠A=∠DCE C.∠D=∠DCE D.∠D+∠ACD=180°
3.对于图中标记的各角,下列条件能够推理得到a∥b的是( A )
A.∠2+∠3=∠4 B.∠2=∠4
C.∠1=∠4 D.∠3=∠4
4.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( B )
A.AD∥BC B.AB∥CD C.CA平分∠BCD D.AC平分∠BAD
第4题图 第5题图 第7题图
5.如图,已知直线AB,CD被直线EF所截,∠AEF=∠CFH,∠1=∠2,则图中所有的平行线有( C )
A.AB∥CD B.PE∥QF
C.AB∥CD和PE∥QF D.PE∥CD
6.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列选项成立的是( C )
A.a⊥c B.b⊥d C.a⊥d D.以上都不对
【解析】∵a⊥b,b⊥c,∴a∥c.
∵b⊥c,c⊥d,∴b∥d.
∵b∥d,a⊥b,
∴a⊥d.故C正确.
7.如图,由图中的数据,可知平行的直线是____________.
【答案】EF和GH
8.已知某品牌遮阳伞的剖面示意图如图所示,若AG同时平分∠BAC与∠EDF,且∠BAC=∠EDF,判断AC,DF是否平行,并说明理由.
解:AC∥DF.理由如下:
∵AG平分∠BAC,∴∠GAC=∠BAC.
∵AG平分∠EDF,∴∠GDF=∠EDF.
∵∠BAC=∠EDF,
∴∠GAC=∠GDF.∴AC∥DF.
9.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( B )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短在同一平面内,垂直于同一条
直线的两条直线互相平行
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
第9题图 第11题图 第12题图
10.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( A )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次左拐50°,第二次左拐130°
11.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,要使直线b与直线c平行,可将直线b绕点A逆时针旋转( A )
A.15° B.30° C.45° D.60°
12.小明把一副三角板按如图所示的方式摆放,其中BC,DF在同一条直线上,可以得到______∥______,依据是_____________________________________________.
【答案】AC DE 在同一平面内,垂直于同一条直线的两条直线互相平行
13.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
解:∵BE平分∠ABD,
∴∠ABE=∠DBE(______________________).
∵∠ABE=∠C,
∴∠DBE=∠C(等量代换),
∴BE∥AC(____________________________).
【答案】角平分线的定义
同位角相等,两直线平行
14.如图,已知直线l1,l2被直线AB所截,交点分别为A,B,AC⊥l2于点C.若∠1=50°,∠2=40°,则l1与l2平行吗?请说明理由.
解:l1∥l2.理由如下:如图.
∵∠1=50°,∠2=40°,
∴∠3=180°-∠1-∠2=90°,
∴AC⊥l1. 又∵AC⊥l2,∴l1∥l2.
15.已知:如图,AD是∠BAC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.
试说明:GE∥AD.
解:∵∠FAG+∠BAC=180°,∠FAG+∠G+∠AFG=180°,
∴∠BAC=∠G+∠AFG
又∵∠AFG=∠G,
∴∠BAC=2∠G.
∵AD是∠BAC的平分线,
∴∠BAC=2∠DAC,
∴2∠G=2∠DAC(等量代换).
∴∠G=∠DAC.
∴GE∥AD (同位角相等,两直线平行).
16.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2.
(1)请说明AB∥CD.
解:∵AB⊥EF,CD⊥EF,∴AB∥CD.
(2)试问BM与DN是否平行?为什么?
解:BM∥DN.理由如下:
∵AB⊥EF,CD⊥EF,
∴∠ABE=∠CDE=90°.
∵∠1=∠2,∴∠ABE-∠1=∠CDE-∠2,即∠MBE=∠NDE.
∴BM∥DN.
17.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.
问:CE与DF的位置关系怎样?试说明理由.
解:CE∥DF.理由如下:
∵BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ABC,∠BCE=∠ACB.
∵∠ABC=∠ACB,∴∠DBC=∠BCE.
∵∠DBF=∠F,∴∠BCE=∠F.
∴CE∥DF.
18.(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由;
解:AB∥CD.理由如下.
∵AB⊥EF,CD⊥EF,∴AB∥CD.
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
解:如图,延长NO′交AB于点P.
∵OM平分∠EOB,O′N平分∠CO′F,
∴∠EOM=∠FO′N=45°.
∵∠FO′N=∠EO′P,
∴∠EOM=∠EO′P=45°.
∴OM∥O′N.
19.如图,EF⊥BC于点F,DE⊥AB,DE交BC于点D.若∠B=∠ADE,则AD与EF平行吗?请说明理由.
解:AD∥EF.理由如下:
∵EF⊥BC,∴∠EFB=90°.
∴∠B+∠BEF=90°.
∵DE⊥AB,∴∠DEA=90°.
∴∠ADE+∠DAB=90°.
∵∠B=∠ADE,∴∠BEF=∠DAB.∴AD∥EF.
20.如图,MN⊥AB于点D,∠ABC=120°,∠BCF=30°,试判断直线MN与EF的位置关系,并说明理由.
解:MN∥EF. 理由如下:延长AB交EF于点G.
∵∠ABC=120°,
∴∠GBC=180°-∠ABC=60°.
∵∠GBC+∠BGC+∠BCF=180°,∠BCF=30°,
∴∠BGC=180°-∠GBC-∠BCF=90°,∴AG⊥EF.
又∵AB⊥MN,∴MN∥EF.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
