1.3.2 利用内错角、同旁内角判定两直线平行 同步练习(含答案)
文档属性
| 名称 | 1.3.2 利用内错角、同旁内角判定两直线平行 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 19:11:57 | ||
图片预览



文档简介
1.3 平行线的判定
第2课时 利用内错角、同旁内角判定两直线平行
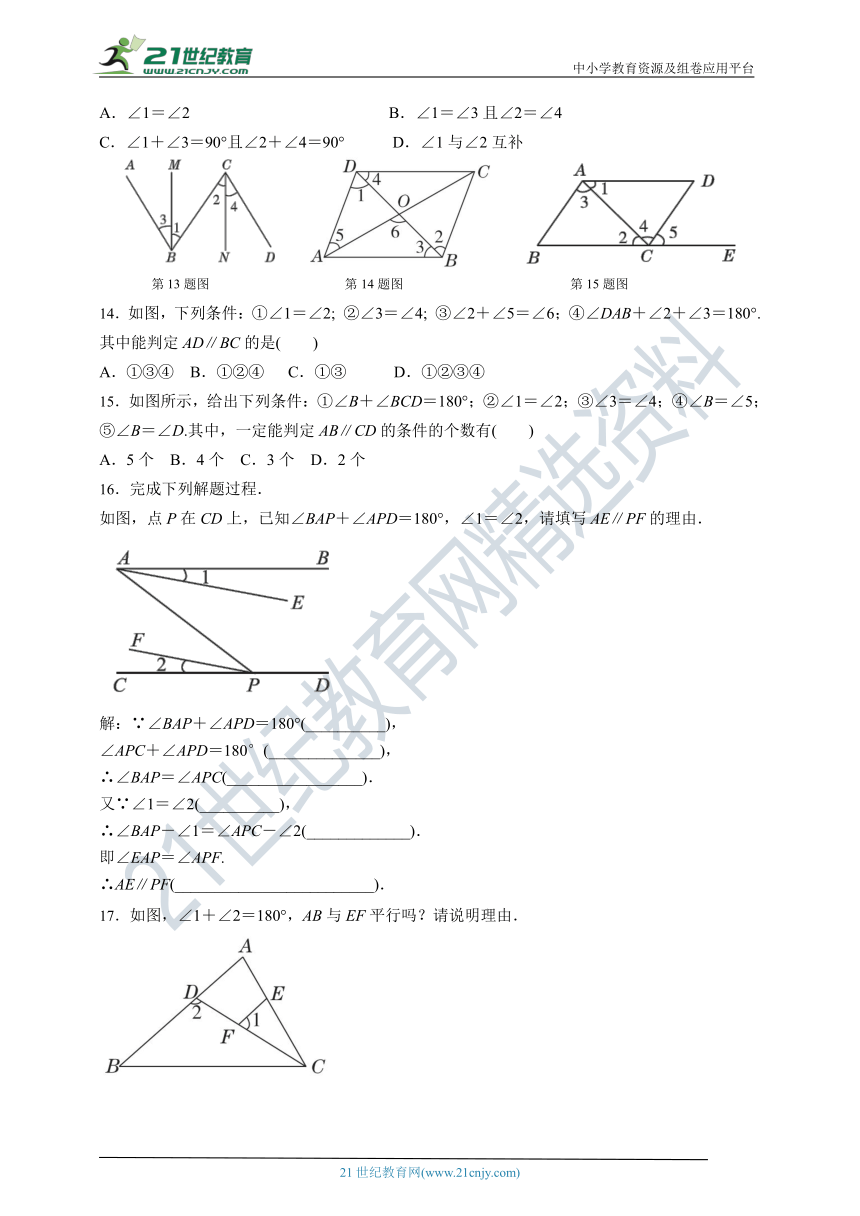
1.下列图形中,由∠1=∠2能得到AB∥CD的是( )
2.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠A=∠ABE D.∠C=∠ABC
第2题图 第4题图 第5题图
3.如图,下列四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图①,展开后测得∠1=∠2 B.如图②,展开后测得∠1=∠2且∠3=∠4
C.如图③,测得∠1=∠2 D.如图④,展开后测得∠1+∠2=180°
4.如图,在四边形ABCD中,连结AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
5.如图,已知∠1=∠2,∠3=∠4,那么下列结论成立的是( )
A.∠1=∠3 B.AE∥CD C.AB∥CD D.AE∥DF
6.小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到________,依据是__________________________.
第6题图 第7题图 第8题图
7.如图,已知∠ACB=∠ABC,∠A=68°,则当∠ECB=________°时,AB∥CE.
8.如图,AE平分∠BAC交BD于点E.若∠2=122°,要使AC∥BD,则∠1=________°.
9.如图,点E在AC上,且∠A=∠CED+∠D.AB与CD平行吗?请说明理由.
10.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若要使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15° B.30° C.45° D.60°
第10题图 第11题图 第12题图
11.如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
12.如图,点E在BC的延长线上,下列条件中,能判定CD∥AB的是( )
①∠1=∠4;②∠2=∠3;③∠5=∠B;
④∠DCB+∠B=180°.
A.①②③④ B.①②③ C.①③④ D.①②
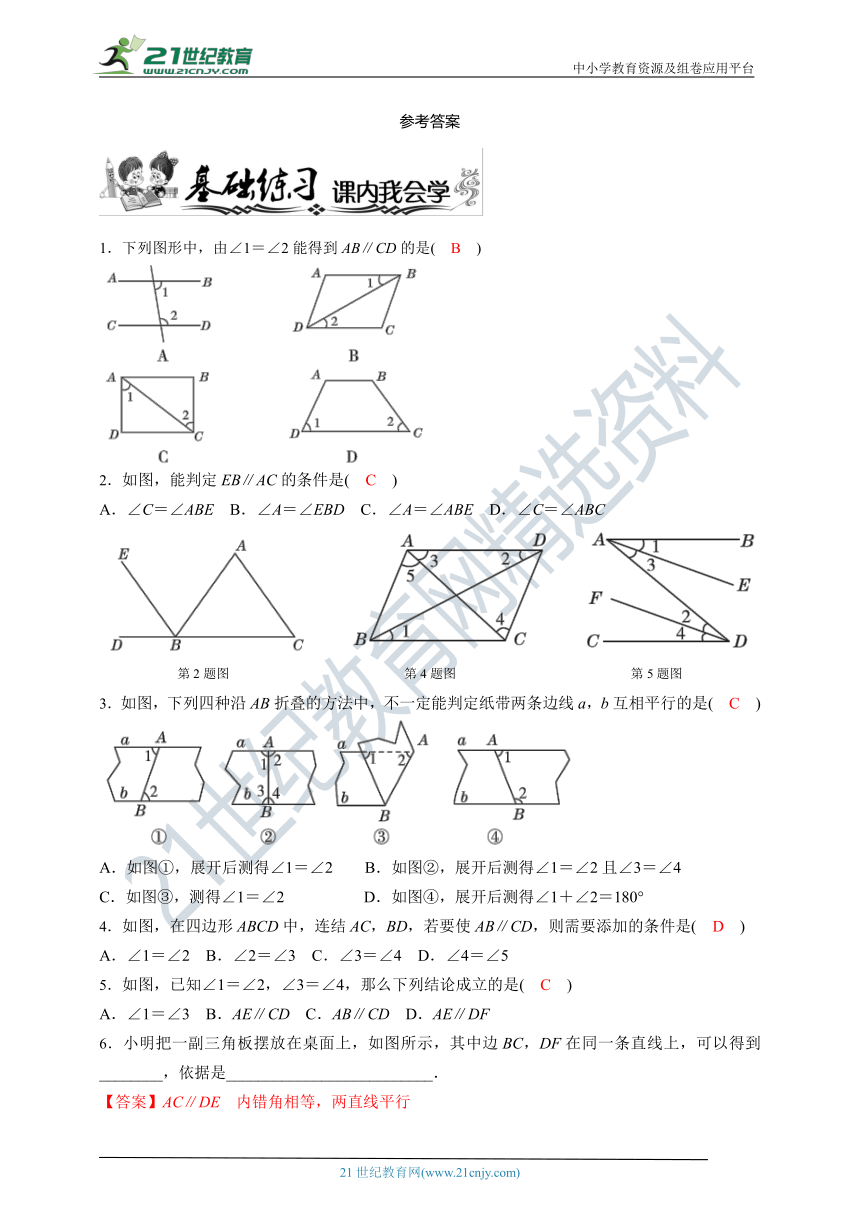
13.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1与∠2互补
第13题图 第14题图 第15题图
14.如图,下列条件:①∠1=∠2; ②∠3=∠4; ③∠2+∠5=∠6;④∠DAB+∠2+∠3=180°.其中能判定AD∥BC的是( )
A.①③④ B.①②④ C.①③ D.①②③④
15.如图所示,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件的个数有( )
A.5个 B.4个 C.3个 D.2个
16.完成下列解题过程.
如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.
解:∵∠BAP+∠APD=180°(__________),
∠APC+∠APD=180°(______________),
∴∠BAP=∠APC(_________________).
又∵∠1=∠2(__________),
∴∠BAP-∠1=∠APC-∠2(_____________).
即∠EAP=∠APF.
∴AE∥PF(_________________________).
17.如图,∠1+∠2=180°,AB与EF平行吗?请说明理由.
18.如图,已知∠DAC=∠ACB,∠D+∠DFE=180°,试说明:EF∥BC.
19.我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中同样如此.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3,请判断c与d是否平行,并说明理由.
20.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,试说明AB∥EF的理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列图形中,由∠1=∠2能得到AB∥CD的是( B )
2.如图,能判定EB∥AC的条件是( C )
A.∠C=∠ABE B.∠A=∠EBD C.∠A=∠ABE D.∠C=∠ABC
第2题图 第4题图 第5题图
3.如图,下列四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( C )
A.如图①,展开后测得∠1=∠2 B.如图②,展开后测得∠1=∠2且∠3=∠4
C.如图③,测得∠1=∠2 D.如图④,展开后测得∠1+∠2=180°
4.如图,在四边形ABCD中,连结AC,BD,若要使AB∥CD,则需要添加的条件是( D )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
5.如图,已知∠1=∠2,∠3=∠4,那么下列结论成立的是( C )
A.∠1=∠3 B.AE∥CD C.AB∥CD D.AE∥DF
6.小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到________,依据是__________________________.
【答案】AC∥DE 内错角相等,两直线平行
第6题图 第7题图 第8题图
7.如图,已知∠ACB=∠ABC,∠A=68°,则当∠ECB=________°时,AB∥CE.
【答案】56
8.如图,AE平分∠BAC交BD于点E.若∠2=122°,要使AC∥BD,则∠1=________°.
【答案】64
9.如图,点E在AC上,且∠A=∠CED+∠D.AB与CD平行吗?请说明理由.
解:AB∥CD.
理由:∵∠C+∠CED+∠D=180°,
∴∠C=180°-(∠CED+∠D).
又∵∠A=∠CED+∠D,
∴∠A+∠C=180°,∴AB∥CD(同旁内角互补,两直线平行).
10.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若要使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A )
A.15° B.30° C.45° D.60°
第10题图 第11题图 第12题图
11.如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( C )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
【解析】∠1=∠2可判定AB∥CD,∠DAB+∠D=180°可判定AB∥CD,∠3=∠4可判定AD∥BC,∠B=∠DCE可判定AB∥CD,故选C.
12.如图,点E在BC的延长线上,下列条件中,能判定CD∥AB的是( C )
①∠1=∠4;②∠2=∠3;③∠5=∠B;
④∠DCB+∠B=180°.
A.①②③④ B.①②③ C.①③④ D.①②
13.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( D )
A.∠1=∠2 B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1与∠2互补
第13题图 第14题图 第15题图
14.如图,下列条件:①∠1=∠2; ②∠3=∠4; ③∠2+∠5=∠6;④∠DAB+∠2+∠3=180°.其中能判定AD∥BC的是( A )
A.①③④ B.①②④ C.①③ D.①②③④
15.如图所示,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件的个数有( C )
A.5个 B.4个 C.3个 D.2个
16.完成下列解题过程.
如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.
解:∵∠BAP+∠APD=180°(__________),
∠APC+∠APD=180°(______________),
∴∠BAP=∠APC(_________________).
又∵∠1=∠2(__________),
∴∠BAP-∠1=∠APC-∠2(_____________).
即∠EAP=∠APF.
∴AE∥PF(_________________________).
【答案】已知 邻补角的性质 同角的补角相等 已知 等式的性质 内错角相等,两直线平行
17.如图,∠1+∠2=180°,AB与EF平行吗?请说明理由.
解:AB∥EF.
理由:∵∠1+∠2=180°,
∠DFE+∠1=180°,
∴∠2=∠DFE,∴AB∥EF.
18.如图,已知∠DAC=∠ACB,∠D+∠DFE=180°,试说明:EF∥BC.
解:∵∠DAC=∠ACB,
∴AD∥BC.∴∠D+∠BCD=180°.
又∵∠D+∠DFE=180°,
∴∠BCD=∠DFE.∴EF∥BC.
19.我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中同样如此.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3,请判断c与d是否平行,并说明理由.
解:c∥d.理由如下:如图,
∵∠2+∠5=∠3+∠6=180°,∠2=∠3,
∴∠5=∠6(等角的补角相等).
∵∠1=∠4,
∴∠1+∠5=∠4+∠6,
∴c∥d(内错角相等,两直线平行).
20.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,试说明AB∥EF的理由.
解:如图,双向延长CD交AB与EF于G,H两点,
∵∠BGC+∠B+∠GCB=180°,
∠GCB+∠BCD=180°,
∴∠BGC+∠B=∠BCD.
∵∠B=25°,∠BCD=45°,
∴∠BGC=20°.
同理可得:∠CDE=∠E+∠DHE.
∵∠CDE=30°,∠E=10°,∴∠DHE=20°.
∴∠BGC=∠DHE,
∴AB∥EF.
第2课时 利用内错角、同旁内角判定两直线平行
1.下列图形中,由∠1=∠2能得到AB∥CD的是( )
2.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠A=∠ABE D.∠C=∠ABC
第2题图 第4题图 第5题图
3.如图,下列四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图①,展开后测得∠1=∠2 B.如图②,展开后测得∠1=∠2且∠3=∠4
C.如图③,测得∠1=∠2 D.如图④,展开后测得∠1+∠2=180°
4.如图,在四边形ABCD中,连结AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
5.如图,已知∠1=∠2,∠3=∠4,那么下列结论成立的是( )
A.∠1=∠3 B.AE∥CD C.AB∥CD D.AE∥DF
6.小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到________,依据是__________________________.
第6题图 第7题图 第8题图
7.如图,已知∠ACB=∠ABC,∠A=68°,则当∠ECB=________°时,AB∥CE.
8.如图,AE平分∠BAC交BD于点E.若∠2=122°,要使AC∥BD,则∠1=________°.
9.如图,点E在AC上,且∠A=∠CED+∠D.AB与CD平行吗?请说明理由.
10.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若要使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15° B.30° C.45° D.60°
第10题图 第11题图 第12题图
11.如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
12.如图,点E在BC的延长线上,下列条件中,能判定CD∥AB的是( )
①∠1=∠4;②∠2=∠3;③∠5=∠B;
④∠DCB+∠B=180°.
A.①②③④ B.①②③ C.①③④ D.①②
13.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1与∠2互补
第13题图 第14题图 第15题图
14.如图,下列条件:①∠1=∠2; ②∠3=∠4; ③∠2+∠5=∠6;④∠DAB+∠2+∠3=180°.其中能判定AD∥BC的是( )
A.①③④ B.①②④ C.①③ D.①②③④
15.如图所示,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件的个数有( )
A.5个 B.4个 C.3个 D.2个
16.完成下列解题过程.
如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.
解:∵∠BAP+∠APD=180°(__________),
∠APC+∠APD=180°(______________),
∴∠BAP=∠APC(_________________).
又∵∠1=∠2(__________),
∴∠BAP-∠1=∠APC-∠2(_____________).
即∠EAP=∠APF.
∴AE∥PF(_________________________).
17.如图,∠1+∠2=180°,AB与EF平行吗?请说明理由.
18.如图,已知∠DAC=∠ACB,∠D+∠DFE=180°,试说明:EF∥BC.
19.我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中同样如此.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3,请判断c与d是否平行,并说明理由.
20.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,试说明AB∥EF的理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列图形中,由∠1=∠2能得到AB∥CD的是( B )
2.如图,能判定EB∥AC的条件是( C )
A.∠C=∠ABE B.∠A=∠EBD C.∠A=∠ABE D.∠C=∠ABC
第2题图 第4题图 第5题图
3.如图,下列四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( C )
A.如图①,展开后测得∠1=∠2 B.如图②,展开后测得∠1=∠2且∠3=∠4
C.如图③,测得∠1=∠2 D.如图④,展开后测得∠1+∠2=180°
4.如图,在四边形ABCD中,连结AC,BD,若要使AB∥CD,则需要添加的条件是( D )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5
5.如图,已知∠1=∠2,∠3=∠4,那么下列结论成立的是( C )
A.∠1=∠3 B.AE∥CD C.AB∥CD D.AE∥DF
6.小明把一副三角板摆放在桌面上,如图所示,其中边BC,DF在同一条直线上,可以得到________,依据是__________________________.
【答案】AC∥DE 内错角相等,两直线平行
第6题图 第7题图 第8题图
7.如图,已知∠ACB=∠ABC,∠A=68°,则当∠ECB=________°时,AB∥CE.
【答案】56
8.如图,AE平分∠BAC交BD于点E.若∠2=122°,要使AC∥BD,则∠1=________°.
【答案】64
9.如图,点E在AC上,且∠A=∠CED+∠D.AB与CD平行吗?请说明理由.
解:AB∥CD.
理由:∵∠C+∠CED+∠D=180°,
∴∠C=180°-(∠CED+∠D).
又∵∠A=∠CED+∠D,
∴∠A+∠C=180°,∴AB∥CD(同旁内角互补,两直线平行).
10.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若要使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A )
A.15° B.30° C.45° D.60°
第10题图 第11题图 第12题图
11.如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( C )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
【解析】∠1=∠2可判定AB∥CD,∠DAB+∠D=180°可判定AB∥CD,∠3=∠4可判定AD∥BC,∠B=∠DCE可判定AB∥CD,故选C.
12.如图,点E在BC的延长线上,下列条件中,能判定CD∥AB的是( C )
①∠1=∠4;②∠2=∠3;③∠5=∠B;
④∠DCB+∠B=180°.
A.①②③④ B.①②③ C.①③④ D.①②
13.如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( D )
A.∠1=∠2 B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90° D.∠1与∠2互补
第13题图 第14题图 第15题图
14.如图,下列条件:①∠1=∠2; ②∠3=∠4; ③∠2+∠5=∠6;④∠DAB+∠2+∠3=180°.其中能判定AD∥BC的是( A )
A.①③④ B.①②④ C.①③ D.①②③④
15.如图所示,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件的个数有( C )
A.5个 B.4个 C.3个 D.2个
16.完成下列解题过程.
如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.
解:∵∠BAP+∠APD=180°(__________),
∠APC+∠APD=180°(______________),
∴∠BAP=∠APC(_________________).
又∵∠1=∠2(__________),
∴∠BAP-∠1=∠APC-∠2(_____________).
即∠EAP=∠APF.
∴AE∥PF(_________________________).
【答案】已知 邻补角的性质 同角的补角相等 已知 等式的性质 内错角相等,两直线平行
17.如图,∠1+∠2=180°,AB与EF平行吗?请说明理由.
解:AB∥EF.
理由:∵∠1+∠2=180°,
∠DFE+∠1=180°,
∴∠2=∠DFE,∴AB∥EF.
18.如图,已知∠DAC=∠ACB,∠D+∠DFE=180°,试说明:EF∥BC.
解:∵∠DAC=∠ACB,
∴AD∥BC.∴∠D+∠BCD=180°.
又∵∠D+∠DFE=180°,
∴∠BCD=∠DFE.∴EF∥BC.
19.我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中同样如此.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3,请判断c与d是否平行,并说明理由.
解:c∥d.理由如下:如图,
∵∠2+∠5=∠3+∠6=180°,∠2=∠3,
∴∠5=∠6(等角的补角相等).
∵∠1=∠4,
∴∠1+∠5=∠4+∠6,
∴c∥d(内错角相等,两直线平行).
20.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,试说明AB∥EF的理由.
解:如图,双向延长CD交AB与EF于G,H两点,
∵∠BGC+∠B+∠GCB=180°,
∠GCB+∠BCD=180°,
∴∠BGC+∠B=∠BCD.
∵∠B=25°,∠BCD=45°,
∴∠BGC=20°.
同理可得:∠CDE=∠E+∠DHE.
∵∠CDE=30°,∠E=10°,∴∠DHE=20°.
∴∠BGC=∠DHE,
∴AB∥EF.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
