1.4.1 两直线平行,同位角相等 同步练习(含答案)
文档属性
| 名称 | 1.4.1 两直线平行,同位角相等 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 19:21:47 | ||
图片预览




文档简介
1.4 平行线的性质
第1课时 两直线平行,同位角相等
1.如图,已知直线a∥b,∠1=60°,则∠2的度数是( )
A.45° B.55° C.60° D.120°
第1题图 第2题图 第3题图
2.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
3.如图,已知直线a,b,c,d,c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的大小是( )
A.30° B.40° C.50° D.60°
4.【2021·台州】一把直尺与一块直角三角板按如图所示方式摆放,若∠1=47°,则∠2=( )
A.40° B.43° C.45° D.47°
第4题图 第5题图 第6题图
5.如图,直线a,b被c所截,a∥b,若∠3=3∠2,则∠1的度数为( )
A.30° B.45° C.50° D.60°
6.如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40° B.50° C.150° D.140°
7.如图,AB∥CD,∠α=45°,∠D=∠C,那么∠D=________°,∠C=________°.
第7题图 第8题图
8.有一条长方形纸带,沿AB折叠后如图所示,若∠1=30°,则∠CAB=______°.
9.是某种品牌的标志图案,其中蕴涵着许多几何知识.如图,BC∥AD,BE∥AF.
(1)试说明∠A=∠B;
(2)若∠DOB=132°,求∠A的度数.
10.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( )
A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD
第10题图 第11题图 第12题图
11.如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( )
A.80° B.70° C. 60° D.50°
12.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从点E射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.75°36′ B.75°12′ C.74°36′ D.74°12′
13.【2022·宁波市镇海区蛟川书院期末】一条两边沿互相平行的围巾折叠后的示意图如图所示,已知∠DAB-∠ABC=20°,且DF∥CG,则3∠DAB+∠ABC=( )
A.180° B.150° C.160° D.200°
第13题图 第14题图
14.如图,AB∥CD,EF∥GH,试探究∠1与∠4的数量关系,并说明理由.
解:∠1+∠4=180°.理由如下:
∵AB∥CD,EF∥GH,
∴∠2=∠3,∠________=∠________(________________________).
∴∠2=∠5(__________).
15.【2022·金华市孝顺教育集团期末·学科综合】如图①,赤道式日晷是中国古代最经典和传统的计时仪器,由底座、晷面、晷针三部分组成,其中底座面与日晷所处地地球半径垂直.
(1)晷针与晷面的夹角为__________;
(2)如图②,日晷所处地的纬度α为39.8°,若太阳光(平行光)与日晷底座的夹角为60°,则太阳光和日晷晷面所夹锐角的角度为________.
16.如图,在三角形ABC中,∠A:∠B:∠C=5:3:4,P是三角形ABC内一点,过点P作DE∥AB,分别交AC,BC于点D,E,作FG∥AC,分别交AB,BC于点F,G,作HQ∥BC,分别交AB,AC于点Q,H.则∠1=________,∠2=________,∠3=________.
17.如图,直线AB∥CD,DE∥BC.
(1)判断∠B与∠D的数量关系,并说明理由.
(2)设∠B=(2x+15)°,∠D=(65-3x)°,求∠1的度数.
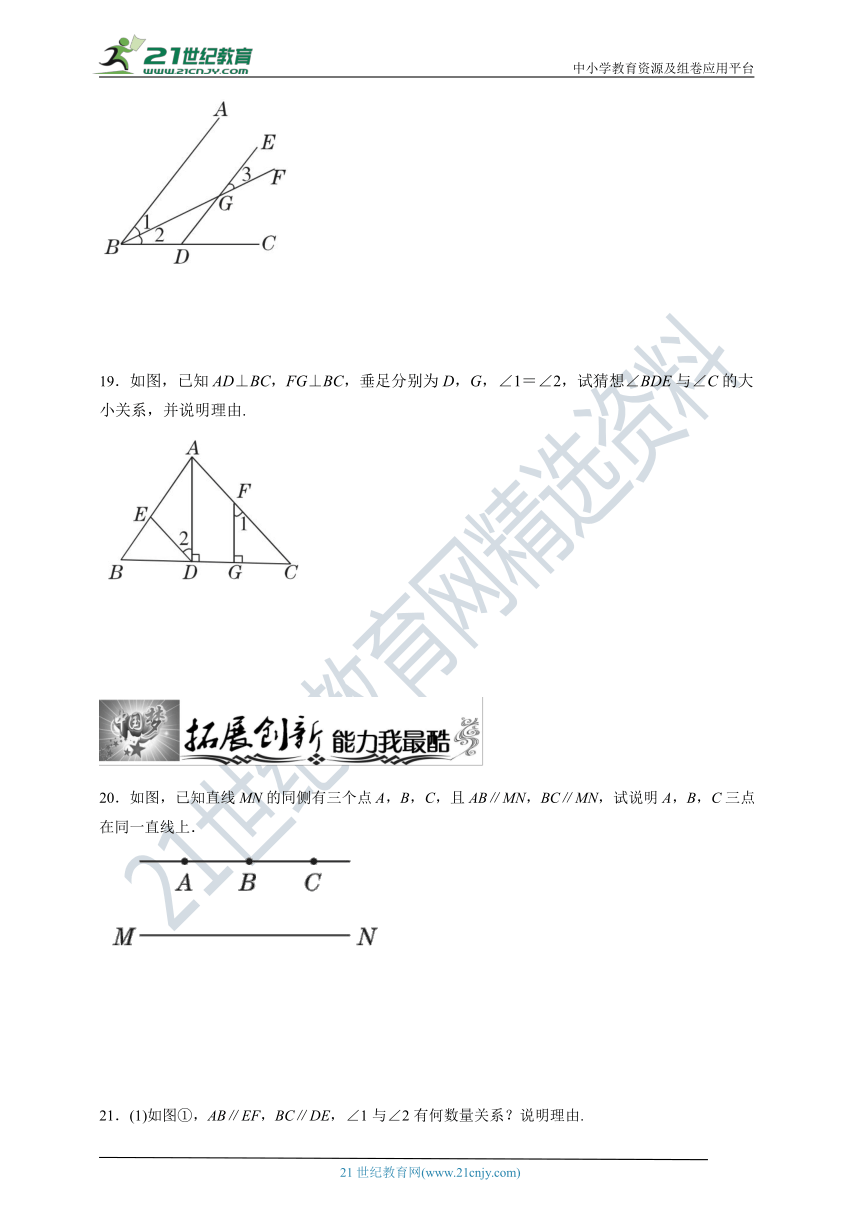
18.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
19.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,试猜想∠BDE与∠C的大小关系,并说明理由.
20.如图,已知直线MN的同侧有三个点A,B,C,且AB∥MN,BC∥MN,试说明A,B,C三点在同一直线上.
21.(1)如图①,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
(2)如图②,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
(3)由(1)(2)可得结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角______________.
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,求这两个角的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,已知直线a∥b,∠1=60°,则∠2的度数是( C )
A.45° B.55° C.60° D.120°
第1题图 第2题图 第3题图
2.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( C )
A.36° B.52° C.72° D.80°
3.如图,已知直线a,b,c,d,c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的大小是( C )
A.30° B.40° C.50° D.60°
4.【2021·台州】一把直尺与一块直角三角板按如图所示方式摆放,若∠1=47°,则∠2=( B )
A.40° B.43° C.45° D.47°
第4题图 第5题图 第6题图
5.如图,直线a,b被c所截,a∥b,若∠3=3∠2,则∠1的度数为( B )
A.30° B.45° C.50° D.60°
6.如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( D )
A.40° B.50° C.150° D.140°
7.如图,AB∥CD,∠α=45°,∠D=∠C,那么∠D=________°,∠C=________°.
【答案】45 45
第7题图 第8题图
8.有一条长方形纸带,沿AB折叠后如图所示,若∠1=30°,则∠CAB=______°.
【答案】75
9.是某种品牌的标志图案,其中蕴涵着许多几何知识.如图,BC∥AD,BE∥AF.
(1)试说明∠A=∠B;
解:∵BC∥AD,
∴∠B=∠DOE.
∵BE∥AF,
∴∠DOE=∠A,
∴∠A=∠B.
(2)若∠DOB=132°,求∠A的度数.
解:∵∠DOB=132°,
∴∠DOE=180°-∠DOB=48°,
∴∠A=48°.
10.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( B )
A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD
第10题图 第11题图 第12题图
11.如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( B )
A.80° B.70° C. 60° D.50°
12.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从点E射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( B )
A.75°36′ B.75°12′ C.74°36′ D.74°12′
13.【2022·宁波市镇海区蛟川书院期末】一条两边沿互相平行的围巾折叠后的示意图如图所示,已知∠DAB-∠ABC=20°,且DF∥CG,则3∠DAB+∠ABC=( D )
A.180° B.150° C.160° D.200°
第13题图 第14题图
14.如图,AB∥CD,EF∥GH,试探究∠1与∠4的数量关系,并说明理由.
解:∠1+∠4=180°.理由如下:
∵AB∥CD,EF∥GH,
∴∠2=∠3,∠________=∠________(________________________).
∴∠2=∠5(__________).
【答案】3 5 两直线平行,同位角相等 等量代换
15.【2022·金华市孝顺教育集团期末·学科综合】如图①,赤道式日晷是中国古代最经典和传统的计时仪器,由底座、晷面、晷针三部分组成,其中底座面与日晷所处地地球半径垂直.
(1)晷针与晷面的夹角为__________;
(2)如图②,日晷所处地的纬度α为39.8°,若太阳光(平行光)与日晷底座的夹角为60°,则太阳光和日晷晷面所夹锐角的角度为________.
【答案】90° 9.8°
16.如图,在三角形ABC中,∠A:∠B:∠C=5:3:4,P是三角形ABC内一点,过点P作DE∥AB,分别交AC,BC于点D,E,作FG∥AC,分别交AB,BC于点F,G,作HQ∥BC,分别交AB,AC于点Q,H.则∠1=________,∠2=________,∠3=________.
【答案】45° 60° 75°
17.如图,直线AB∥CD,DE∥BC.
(1)判断∠B与∠D的数量关系,并说明理由.
解:∠B=∠D.
理由如下:∵AB∥CD,∴∠B=∠1.
∵DE∥BC,∴∠1=∠D.
∴∠B=∠D.
(2)设∠B=(2x+15)°,∠D=(65-3x)°,求∠1的度数.
解:由2x+15=65-3x,解得x=10,
∴∠B=35°.∴∠1=35°.
18.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
解:∵BF平分∠ABC,∠2=26°,
∴∠1=∠2,∠ABC=2∠2=52°.
又∵∠2=∠3,∴∠1=∠3.
∴AB∥DE.∴∠EDC=∠ABC=52°.
19.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,试猜想∠BDE与∠C的大小关系,并说明理由.
解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC,∴AD∥FG.
∴∠1=∠DAC.
又∵∠1=∠2,∴∠2=∠DAC.
∴DE∥AC.∴∠BDE=∠C.
20.如图,已知直线MN的同侧有三个点A,B,C,且AB∥MN,BC∥MN,试说明A,B,C三点在同一直线上.
解:如图,过点B任作一条直线PQ交MN于点Q.
∵AB∥MN,
∴∠PBA=∠PQM.
∵BC∥MN,
∴∠PBC=∠PQN.
∵∠PQM+∠PQN=180°,
∴∠ABC=∠PBA+∠PBC=180°,
∴A,B,C三点在同一直线上.
21.(1)如图①,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
解:∠1=∠2.理由:如图①,
∵AB∥EF,∴∠3=∠2.
∵BC∥DE,∴∠3=∠1.
∴∠1=∠2.
(2)如图②,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
解:∠1+∠2=180°.
理由:如图②,∵AB∥EF,
∴∠2=∠4.
∵BC∥DE,∴∠3=∠1.
∵∠3+∠4=180°,∴∠1+∠2=180°.
(3)由(1)(2)可得结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角______________.
【答案】相等或互补
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,求这两个角的度数.
解:设一个角的度数为x°,另一个角的度数为(2x-60)°.
根据(3)中结论可得2x-60=x或2x-60+x=180,
解得x=60或x=80.
当x=60时,2x-60=60,
当x=80时,2x-60=100.
∴这两个角的度数分别为60°,60° 或100°,80°.
第1课时 两直线平行,同位角相等
1.如图,已知直线a∥b,∠1=60°,则∠2的度数是( )
A.45° B.55° C.60° D.120°
第1题图 第2题图 第3题图
2.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
3.如图,已知直线a,b,c,d,c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的大小是( )
A.30° B.40° C.50° D.60°
4.【2021·台州】一把直尺与一块直角三角板按如图所示方式摆放,若∠1=47°,则∠2=( )
A.40° B.43° C.45° D.47°
第4题图 第5题图 第6题图
5.如图,直线a,b被c所截,a∥b,若∠3=3∠2,则∠1的度数为( )
A.30° B.45° C.50° D.60°
6.如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40° B.50° C.150° D.140°
7.如图,AB∥CD,∠α=45°,∠D=∠C,那么∠D=________°,∠C=________°.
第7题图 第8题图
8.有一条长方形纸带,沿AB折叠后如图所示,若∠1=30°,则∠CAB=______°.
9.是某种品牌的标志图案,其中蕴涵着许多几何知识.如图,BC∥AD,BE∥AF.
(1)试说明∠A=∠B;
(2)若∠DOB=132°,求∠A的度数.
10.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( )
A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD
第10题图 第11题图 第12题图
11.如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( )
A.80° B.70° C. 60° D.50°
12.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从点E射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.75°36′ B.75°12′ C.74°36′ D.74°12′
13.【2022·宁波市镇海区蛟川书院期末】一条两边沿互相平行的围巾折叠后的示意图如图所示,已知∠DAB-∠ABC=20°,且DF∥CG,则3∠DAB+∠ABC=( )
A.180° B.150° C.160° D.200°
第13题图 第14题图
14.如图,AB∥CD,EF∥GH,试探究∠1与∠4的数量关系,并说明理由.
解:∠1+∠4=180°.理由如下:
∵AB∥CD,EF∥GH,
∴∠2=∠3,∠________=∠________(________________________).
∴∠2=∠5(__________).
15.【2022·金华市孝顺教育集团期末·学科综合】如图①,赤道式日晷是中国古代最经典和传统的计时仪器,由底座、晷面、晷针三部分组成,其中底座面与日晷所处地地球半径垂直.
(1)晷针与晷面的夹角为__________;
(2)如图②,日晷所处地的纬度α为39.8°,若太阳光(平行光)与日晷底座的夹角为60°,则太阳光和日晷晷面所夹锐角的角度为________.
16.如图,在三角形ABC中,∠A:∠B:∠C=5:3:4,P是三角形ABC内一点,过点P作DE∥AB,分别交AC,BC于点D,E,作FG∥AC,分别交AB,BC于点F,G,作HQ∥BC,分别交AB,AC于点Q,H.则∠1=________,∠2=________,∠3=________.
17.如图,直线AB∥CD,DE∥BC.
(1)判断∠B与∠D的数量关系,并说明理由.
(2)设∠B=(2x+15)°,∠D=(65-3x)°,求∠1的度数.
18.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
19.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,试猜想∠BDE与∠C的大小关系,并说明理由.
20.如图,已知直线MN的同侧有三个点A,B,C,且AB∥MN,BC∥MN,试说明A,B,C三点在同一直线上.
21.(1)如图①,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
(2)如图②,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
(3)由(1)(2)可得结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角______________.
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,求这两个角的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,已知直线a∥b,∠1=60°,则∠2的度数是( C )
A.45° B.55° C.60° D.120°
第1题图 第2题图 第3题图
2.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( C )
A.36° B.52° C.72° D.80°
3.如图,已知直线a,b,c,d,c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的大小是( C )
A.30° B.40° C.50° D.60°
4.【2021·台州】一把直尺与一块直角三角板按如图所示方式摆放,若∠1=47°,则∠2=( B )
A.40° B.43° C.45° D.47°
第4题图 第5题图 第6题图
5.如图,直线a,b被c所截,a∥b,若∠3=3∠2,则∠1的度数为( B )
A.30° B.45° C.50° D.60°
6.如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( D )
A.40° B.50° C.150° D.140°
7.如图,AB∥CD,∠α=45°,∠D=∠C,那么∠D=________°,∠C=________°.
【答案】45 45
第7题图 第8题图
8.有一条长方形纸带,沿AB折叠后如图所示,若∠1=30°,则∠CAB=______°.
【答案】75
9.是某种品牌的标志图案,其中蕴涵着许多几何知识.如图,BC∥AD,BE∥AF.
(1)试说明∠A=∠B;
解:∵BC∥AD,
∴∠B=∠DOE.
∵BE∥AF,
∴∠DOE=∠A,
∴∠A=∠B.
(2)若∠DOB=132°,求∠A的度数.
解:∵∠DOB=132°,
∴∠DOE=180°-∠DOB=48°,
∴∠A=48°.
10.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( B )
A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD
第10题图 第11题图 第12题图
11.如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( B )
A.80° B.70° C. 60° D.50°
12.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从点E射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( B )
A.75°36′ B.75°12′ C.74°36′ D.74°12′
13.【2022·宁波市镇海区蛟川书院期末】一条两边沿互相平行的围巾折叠后的示意图如图所示,已知∠DAB-∠ABC=20°,且DF∥CG,则3∠DAB+∠ABC=( D )
A.180° B.150° C.160° D.200°
第13题图 第14题图
14.如图,AB∥CD,EF∥GH,试探究∠1与∠4的数量关系,并说明理由.
解:∠1+∠4=180°.理由如下:
∵AB∥CD,EF∥GH,
∴∠2=∠3,∠________=∠________(________________________).
∴∠2=∠5(__________).
【答案】3 5 两直线平行,同位角相等 等量代换
15.【2022·金华市孝顺教育集团期末·学科综合】如图①,赤道式日晷是中国古代最经典和传统的计时仪器,由底座、晷面、晷针三部分组成,其中底座面与日晷所处地地球半径垂直.
(1)晷针与晷面的夹角为__________;
(2)如图②,日晷所处地的纬度α为39.8°,若太阳光(平行光)与日晷底座的夹角为60°,则太阳光和日晷晷面所夹锐角的角度为________.
【答案】90° 9.8°
16.如图,在三角形ABC中,∠A:∠B:∠C=5:3:4,P是三角形ABC内一点,过点P作DE∥AB,分别交AC,BC于点D,E,作FG∥AC,分别交AB,BC于点F,G,作HQ∥BC,分别交AB,AC于点Q,H.则∠1=________,∠2=________,∠3=________.
【答案】45° 60° 75°
17.如图,直线AB∥CD,DE∥BC.
(1)判断∠B与∠D的数量关系,并说明理由.
解:∠B=∠D.
理由如下:∵AB∥CD,∴∠B=∠1.
∵DE∥BC,∴∠1=∠D.
∴∠B=∠D.
(2)设∠B=(2x+15)°,∠D=(65-3x)°,求∠1的度数.
解:由2x+15=65-3x,解得x=10,
∴∠B=35°.∴∠1=35°.
18.如图,已知BF平分∠ABC,交DE于点G,∠2=∠3=26°,求∠EDC的度数.
解:∵BF平分∠ABC,∠2=26°,
∴∠1=∠2,∠ABC=2∠2=52°.
又∵∠2=∠3,∴∠1=∠3.
∴AB∥DE.∴∠EDC=∠ABC=52°.
19.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,试猜想∠BDE与∠C的大小关系,并说明理由.
解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC,∴AD∥FG.
∴∠1=∠DAC.
又∵∠1=∠2,∴∠2=∠DAC.
∴DE∥AC.∴∠BDE=∠C.
20.如图,已知直线MN的同侧有三个点A,B,C,且AB∥MN,BC∥MN,试说明A,B,C三点在同一直线上.
解:如图,过点B任作一条直线PQ交MN于点Q.
∵AB∥MN,
∴∠PBA=∠PQM.
∵BC∥MN,
∴∠PBC=∠PQN.
∵∠PQM+∠PQN=180°,
∴∠ABC=∠PBA+∠PBC=180°,
∴A,B,C三点在同一直线上.
21.(1)如图①,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
解:∠1=∠2.理由:如图①,
∵AB∥EF,∴∠3=∠2.
∵BC∥DE,∴∠3=∠1.
∴∠1=∠2.
(2)如图②,AB∥EF,BC∥DE,∠1与∠2有何数量关系?说明理由.
解:∠1+∠2=180°.
理由:如图②,∵AB∥EF,
∴∠2=∠4.
∵BC∥DE,∴∠3=∠1.
∵∠3+∠4=180°,∴∠1+∠2=180°.
(3)由(1)(2)可得结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角______________.
【答案】相等或互补
(4)若两个角的两边分别平行,且一个角比另一个角的2倍少60°,求这两个角的度数.
解:设一个角的度数为x°,另一个角的度数为(2x-60)°.
根据(3)中结论可得2x-60=x或2x-60+x=180,
解得x=60或x=80.
当x=60时,2x-60=60,
当x=80时,2x-60=100.
∴这两个角的度数分别为60°,60° 或100°,80°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
