1.4.2 平行线的内错角、同旁内角性质 同步练习(含答案)
文档属性
| 名称 | 1.4.2 平行线的内错角、同旁内角性质 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 00:00:00 | ||
图片预览


文档简介
1.4 平行线的性质
第2课时 平行线的内错角、同旁内角性质
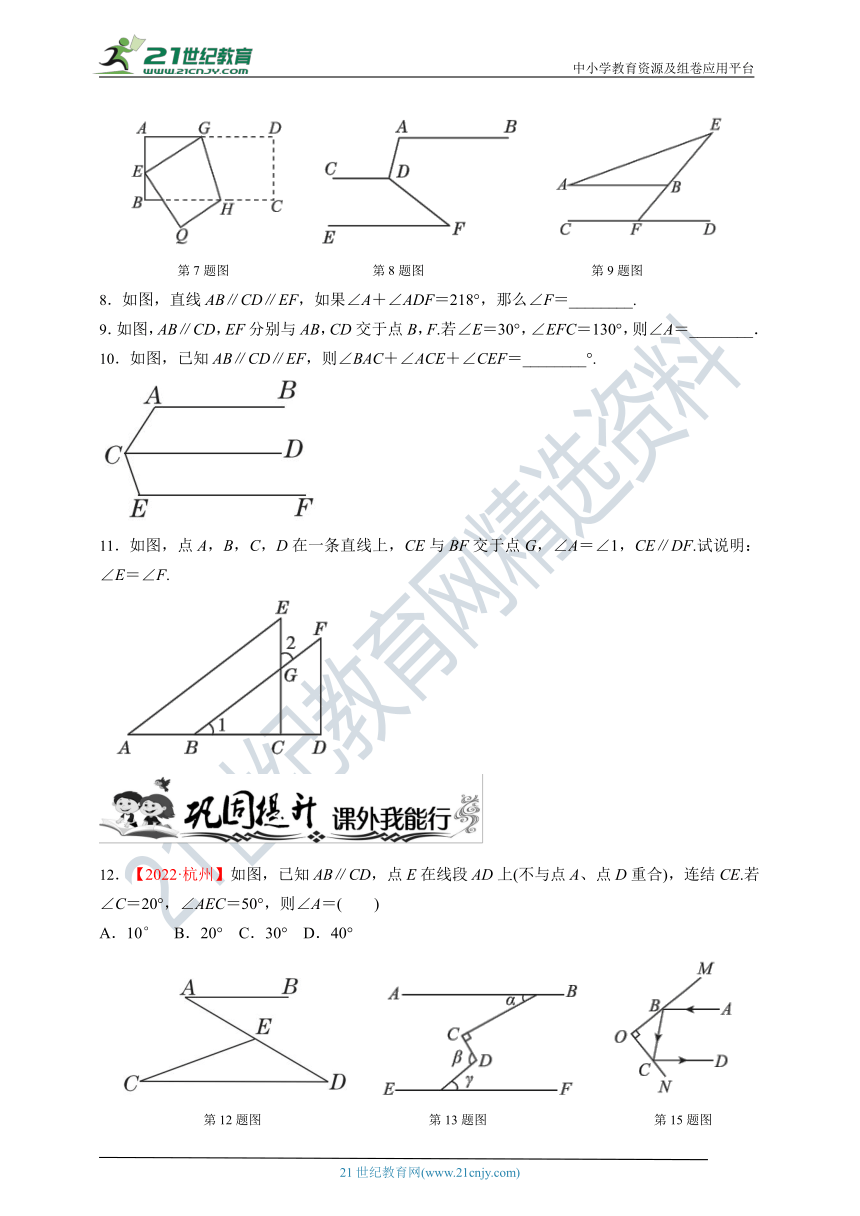
1.如图,已知AB∥CD,下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
第1题图 第2题图 第3题图
2.如图,已知a∥b,则图中与∠1互补的角有( )
A.2个 B.3个 C.4个 D.5个
3.如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( )
A.45° B.60° C.75° D.85°
4.【2022·绍兴】如图,把一块直角三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
第4题图 第5题图 第6题图
5.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
A.50° B.45° C.40° D.30°
6.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为( )
A.10° B.20° C.30° D.40°
7.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
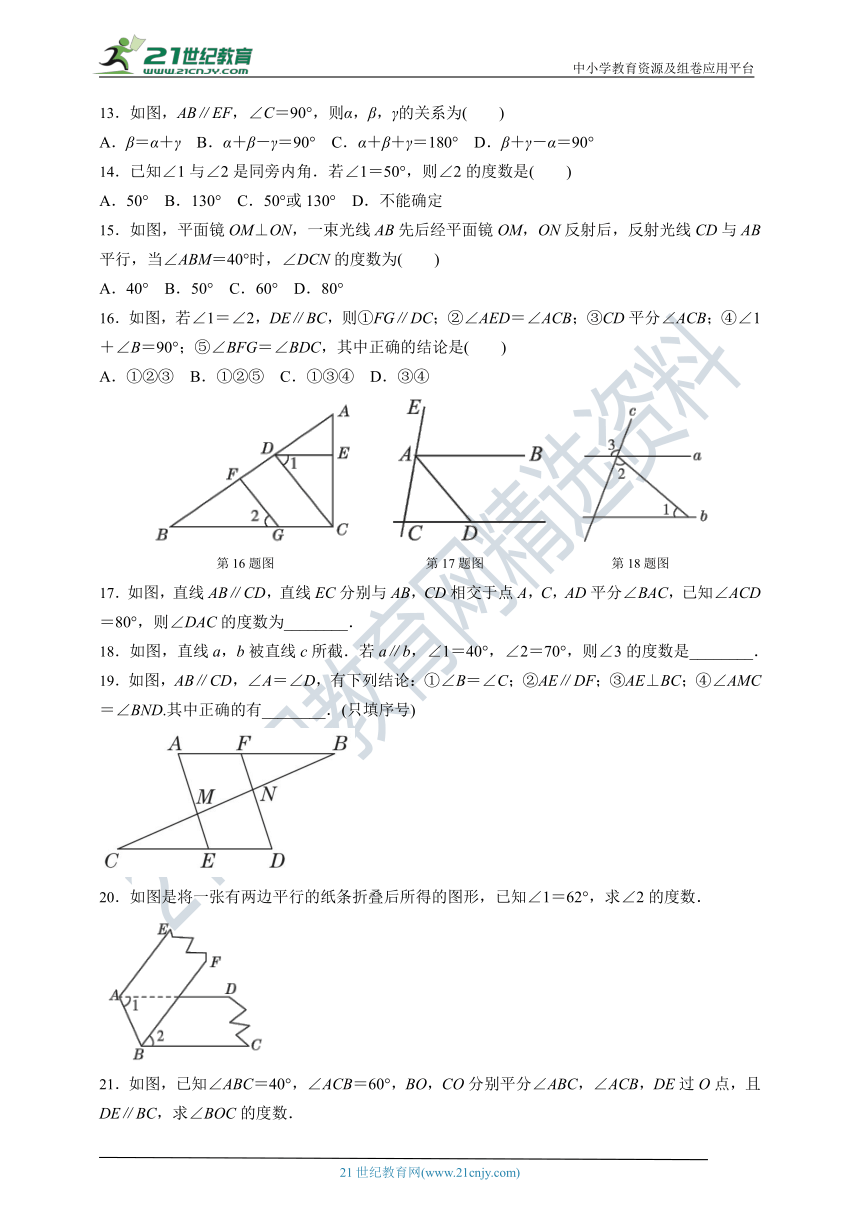
第7题图 第8题图 第9题图
8.如图,直线AB∥CD∥EF,如果∠A+∠ADF=218°,那么∠F=________.
9.如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=________.
10.如图,已知AB∥CD∥EF,则∠BAC+∠ACE+∠CEF=________°.
11.如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.试说明:∠E=∠F.
12.【2022·杭州】如图,已知AB∥CD,点E在线段AD上(不与点A、点D重合),连结CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
第12题图 第13题图 第15题图
13.如图,AB∥EF,∠C=90°,则α,β,γ的关系为( )
A.β=α+γ B.α+β-γ=90° C.α+β+γ=180° D.β+γ-α=90°
14.已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
15.如图,平面镜OM⊥ON,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )
A.40° B.50° C.60° D.80°
16.如图,若∠1=∠2,DE∥BC,则①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )
A.①②③ B.①②⑤ C.①③④ D.③④
第16题图 第17题图 第18题图
17.如图,直线AB∥CD,直线EC分别与AB,CD相交于点A,C,AD平分∠BAC,已知∠ACD=80°,则∠DAC的度数为________.
18.如图,直线a,b被直线c所截.若a∥b,∠1=40°,∠2=70°,则∠3的度数是________.
19.如图,AB∥CD,∠A=∠D,有下列结论:①∠B=∠C;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有________.(只填序号)
20.如图是将一张有两边平行的纸条折叠后所得的图形,已知∠1=62°,求∠2的度数.
21.如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.
22.有一天小明同学用《几何画板》画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连结BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②③④所示的图形.这时他突然一想:∠B,∠D与∠BED之间是否存在某种数量关系呢?接着小明同学通过《几何画板》的“度量角度”和“计算”等功能,找到了这三个角之间的数量关系.
(1)请你探讨图①至图④中,∠B,∠D与∠BED之间的数量关系.图①中,∠BED=__________;图②中,∠BED=________________;图③中,∠BED=__________;图④中,∠BED=__________.
(2)选图③说明你发现的数量关系:
如图⑤,过点E作EF∥AB,
则∠FEB=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
又∵∠BED=________________,
∴∠BED=____________.
(3)仿照(2)中的解答过程,说明你在图④中发现的数量关系.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
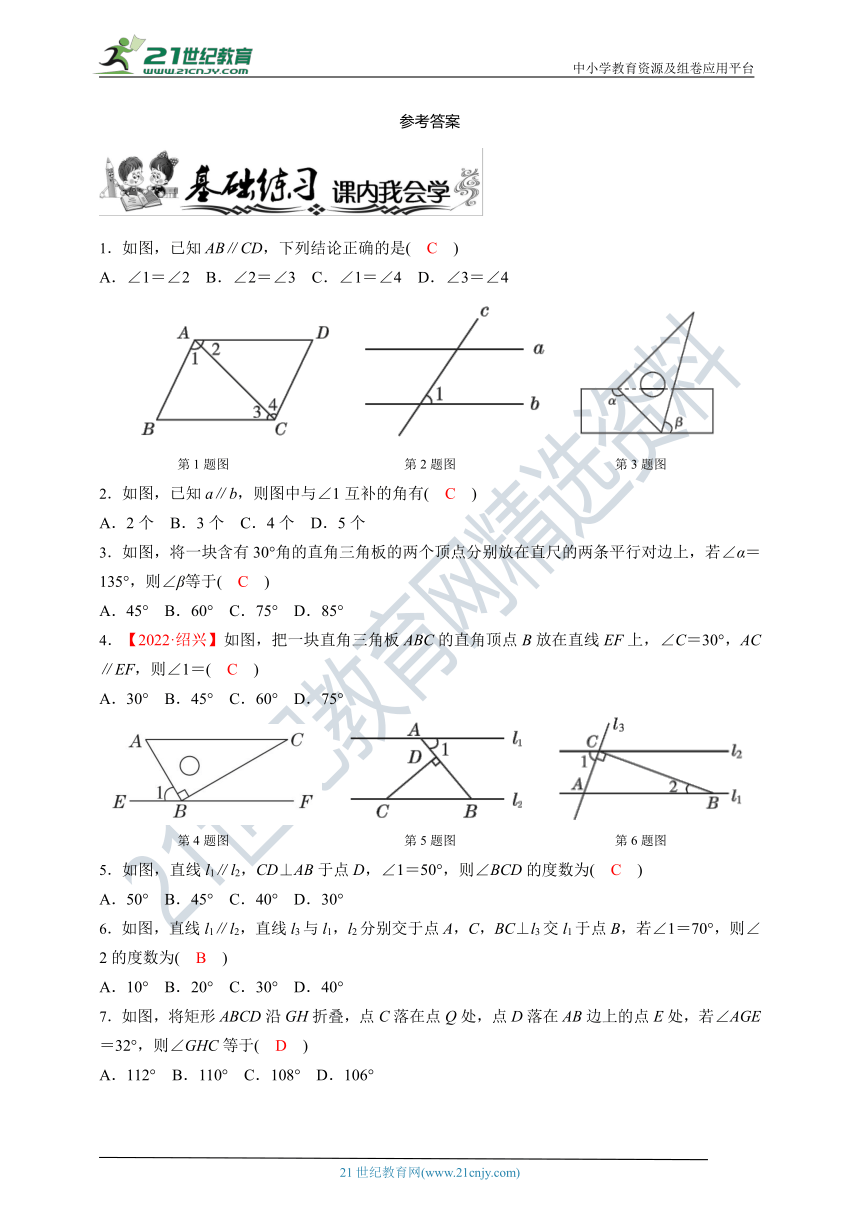
1.如图,已知AB∥CD,下列结论正确的是( C )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
第1题图 第2题图 第3题图
2.如图,已知a∥b,则图中与∠1互补的角有( C )
A.2个 B.3个 C.4个 D.5个
3.如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( C )
A.45° B.60° C.75° D.85°
4.【2022·绍兴】如图,把一块直角三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( C )
A.30° B.45° C.60° D.75°
第4题图 第5题图 第6题图
5.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( C )
A.50° B.45° C.40° D.30°
6.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为( B )
A.10° B.20° C.30° D.40°
7.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( D )
A.112° B.110° C.108° D.106°
第7题图 第8题图 第9题图
8.如图,直线AB∥CD∥EF,如果∠A+∠ADF=218°,那么∠F=________.
【答案】38°
9.如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=________.
【答案】20°
10.如图,已知AB∥CD∥EF,则∠BAC+∠ACE+∠CEF=________°.
【答案】360
11.如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.试说明:∠E=∠F.
解:∵∠A=∠1,
∴AE∥BF.∴∠E=∠2.
∵CE∥DF,∴∠2=∠F.
∴∠E=∠F.
12.【2022·杭州】如图,已知AB∥CD,点E在线段AD上(不与点A、点D重合),连结CE.若∠C=20°,∠AEC=50°,则∠A=( C )
A.10° B.20° C.30° D.40°
第12题图 第13题图 第15题图
13.如图,AB∥EF,∠C=90°,则α,β,γ的关系为( B )
A.β=α+γ B.α+β-γ=90° C.α+β+γ=180° D.β+γ-α=90°
14.已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( D )
A.50° B.130° C.50°或130° D.不能确定
15.如图,平面镜OM⊥ON,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( B )
A.40° B.50° C.60° D.80°
16.如图,若∠1=∠2,DE∥BC,则①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( B )
A.①②③ B.①②⑤ C.①③④ D.③④
【解析】∵DE∥BC,∴∠DCB=∠1,∠AED=∠ACB,故②正确;∵∠1=∠2,∴∠2=∠DCB,∴FG∥DC,故①正确;∴∠BFG=∠BDC,故⑤正确;而CD不一定平分∠ACB,∠1+∠B不一定等于90°,故③④错误,故选B.
第16题图 第17题图 第18题图
17.如图,直线AB∥CD,直线EC分别与AB,CD相交于点A,C,AD平分∠BAC,已知∠ACD=80°,则∠DAC的度数为________.
【答案】50°
18.如图,直线a,b被直线c所截.若a∥b,∠1=40°,∠2=70°,则∠3的度数是________.
【答案】110°
19.如图,AB∥CD,∠A=∠D,有下列结论:①∠B=∠C;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有________.(只填序号)
【答案】①②④
20.如图是将一张有两边平行的纸条折叠后所得的图形,已知∠1=62°,求∠2的度数.
解:延长CB至点G.
∵AD∥BC,∠1=62°,
∴∠ABG=62°.
由折叠可知∠ABG=∠ABF,
∴∠ABF=62°.
∴∠2=180°-62°-62°=56°.
21.如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.
解:因为DE∥BC,所以∠DOB=∠OBC,
∠EOC=∠OCB.
因为BO,CO分别平分∠ABC,∠ACB,
所以∠OBC=∠ABC=20°,∠OCB=∠ACB=30°,
所以∠DOB=20°,∠EOC=30°,
所以∠BOC=180°-∠DOB-∠EOC=130°.
22.有一天小明同学用《几何画板》画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连结BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②③④所示的图形.这时他突然一想:∠B,∠D与∠BED之间是否存在某种数量关系呢?接着小明同学通过《几何画板》的“度量角度”和“计算”等功能,找到了这三个角之间的数量关系.
(1)请你探讨图①至图④中,∠B,∠D与∠BED之间的数量关系.图①中,∠BED=__________;图②中,∠BED=________________;图③中,∠BED=__________;图④中,∠BED=__________.
【答案】∠B+∠D 360°-∠B-∠D ∠D-∠B ∠B-∠D
(2)选图③说明你发现的数量关系:
如图⑤,过点E作EF∥AB,
则∠FEB=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
又∵∠BED=________________,
∴∠BED=____________.
【答案】∠FED-∠FEB ∠D-∠B
(3)仿照(2)中的解答过程,说明你在图④中发现的数量关系.
解:过点E向左侧作EF∥AB,
则∠FEB=180°-∠B. ∵AB∥CD,∴EF∥CD.
∴∠FED=180°-∠D.
又∵∠BED=∠FED-∠FEB,
∴∠BED=(180°-∠D)-(180°-∠B)=∠B-∠D.
第2课时 平行线的内错角、同旁内角性质
1.如图,已知AB∥CD,下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
第1题图 第2题图 第3题图
2.如图,已知a∥b,则图中与∠1互补的角有( )
A.2个 B.3个 C.4个 D.5个
3.如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( )
A.45° B.60° C.75° D.85°
4.【2022·绍兴】如图,把一块直角三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
第4题图 第5题图 第6题图
5.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
A.50° B.45° C.40° D.30°
6.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为( )
A.10° B.20° C.30° D.40°
7.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
第7题图 第8题图 第9题图
8.如图,直线AB∥CD∥EF,如果∠A+∠ADF=218°,那么∠F=________.
9.如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=________.
10.如图,已知AB∥CD∥EF,则∠BAC+∠ACE+∠CEF=________°.
11.如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.试说明:∠E=∠F.
12.【2022·杭州】如图,已知AB∥CD,点E在线段AD上(不与点A、点D重合),连结CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
第12题图 第13题图 第15题图
13.如图,AB∥EF,∠C=90°,则α,β,γ的关系为( )
A.β=α+γ B.α+β-γ=90° C.α+β+γ=180° D.β+γ-α=90°
14.已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
15.如图,平面镜OM⊥ON,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )
A.40° B.50° C.60° D.80°
16.如图,若∠1=∠2,DE∥BC,则①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )
A.①②③ B.①②⑤ C.①③④ D.③④
第16题图 第17题图 第18题图
17.如图,直线AB∥CD,直线EC分别与AB,CD相交于点A,C,AD平分∠BAC,已知∠ACD=80°,则∠DAC的度数为________.
18.如图,直线a,b被直线c所截.若a∥b,∠1=40°,∠2=70°,则∠3的度数是________.
19.如图,AB∥CD,∠A=∠D,有下列结论:①∠B=∠C;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有________.(只填序号)
20.如图是将一张有两边平行的纸条折叠后所得的图形,已知∠1=62°,求∠2的度数.
21.如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.
22.有一天小明同学用《几何画板》画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连结BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②③④所示的图形.这时他突然一想:∠B,∠D与∠BED之间是否存在某种数量关系呢?接着小明同学通过《几何画板》的“度量角度”和“计算”等功能,找到了这三个角之间的数量关系.
(1)请你探讨图①至图④中,∠B,∠D与∠BED之间的数量关系.图①中,∠BED=__________;图②中,∠BED=________________;图③中,∠BED=__________;图④中,∠BED=__________.
(2)选图③说明你发现的数量关系:
如图⑤,过点E作EF∥AB,
则∠FEB=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
又∵∠BED=________________,
∴∠BED=____________.
(3)仿照(2)中的解答过程,说明你在图④中发现的数量关系.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,已知AB∥CD,下列结论正确的是( C )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
第1题图 第2题图 第3题图
2.如图,已知a∥b,则图中与∠1互补的角有( C )
A.2个 B.3个 C.4个 D.5个
3.如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( C )
A.45° B.60° C.75° D.85°
4.【2022·绍兴】如图,把一块直角三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( C )
A.30° B.45° C.60° D.75°
第4题图 第5题图 第6题图
5.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( C )
A.50° B.45° C.40° D.30°
6.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为( B )
A.10° B.20° C.30° D.40°
7.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( D )
A.112° B.110° C.108° D.106°
第7题图 第8题图 第9题图
8.如图,直线AB∥CD∥EF,如果∠A+∠ADF=218°,那么∠F=________.
【答案】38°
9.如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=________.
【答案】20°
10.如图,已知AB∥CD∥EF,则∠BAC+∠ACE+∠CEF=________°.
【答案】360
11.如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.试说明:∠E=∠F.
解:∵∠A=∠1,
∴AE∥BF.∴∠E=∠2.
∵CE∥DF,∴∠2=∠F.
∴∠E=∠F.
12.【2022·杭州】如图,已知AB∥CD,点E在线段AD上(不与点A、点D重合),连结CE.若∠C=20°,∠AEC=50°,则∠A=( C )
A.10° B.20° C.30° D.40°
第12题图 第13题图 第15题图
13.如图,AB∥EF,∠C=90°,则α,β,γ的关系为( B )
A.β=α+γ B.α+β-γ=90° C.α+β+γ=180° D.β+γ-α=90°
14.已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( D )
A.50° B.130° C.50°或130° D.不能确定
15.如图,平面镜OM⊥ON,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( B )
A.40° B.50° C.60° D.80°
16.如图,若∠1=∠2,DE∥BC,则①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( B )
A.①②③ B.①②⑤ C.①③④ D.③④
【解析】∵DE∥BC,∴∠DCB=∠1,∠AED=∠ACB,故②正确;∵∠1=∠2,∴∠2=∠DCB,∴FG∥DC,故①正确;∴∠BFG=∠BDC,故⑤正确;而CD不一定平分∠ACB,∠1+∠B不一定等于90°,故③④错误,故选B.
第16题图 第17题图 第18题图
17.如图,直线AB∥CD,直线EC分别与AB,CD相交于点A,C,AD平分∠BAC,已知∠ACD=80°,则∠DAC的度数为________.
【答案】50°
18.如图,直线a,b被直线c所截.若a∥b,∠1=40°,∠2=70°,则∠3的度数是________.
【答案】110°
19.如图,AB∥CD,∠A=∠D,有下列结论:①∠B=∠C;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有________.(只填序号)
【答案】①②④
20.如图是将一张有两边平行的纸条折叠后所得的图形,已知∠1=62°,求∠2的度数.
解:延长CB至点G.
∵AD∥BC,∠1=62°,
∴∠ABG=62°.
由折叠可知∠ABG=∠ABF,
∴∠ABF=62°.
∴∠2=180°-62°-62°=56°.
21.如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.
解:因为DE∥BC,所以∠DOB=∠OBC,
∠EOC=∠OCB.
因为BO,CO分别平分∠ABC,∠ACB,
所以∠OBC=∠ABC=20°,∠OCB=∠ACB=30°,
所以∠DOB=20°,∠EOC=30°,
所以∠BOC=180°-∠DOB-∠EOC=130°.
22.有一天小明同学用《几何画板》画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连结BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②③④所示的图形.这时他突然一想:∠B,∠D与∠BED之间是否存在某种数量关系呢?接着小明同学通过《几何画板》的“度量角度”和“计算”等功能,找到了这三个角之间的数量关系.
(1)请你探讨图①至图④中,∠B,∠D与∠BED之间的数量关系.图①中,∠BED=__________;图②中,∠BED=________________;图③中,∠BED=__________;图④中,∠BED=__________.
【答案】∠B+∠D 360°-∠B-∠D ∠D-∠B ∠B-∠D
(2)选图③说明你发现的数量关系:
如图⑤,过点E作EF∥AB,
则∠FEB=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
又∵∠BED=________________,
∴∠BED=____________.
【答案】∠FED-∠FEB ∠D-∠B
(3)仿照(2)中的解答过程,说明你在图④中发现的数量关系.
解:过点E向左侧作EF∥AB,
则∠FEB=180°-∠B. ∵AB∥CD,∴EF∥CD.
∴∠FED=180°-∠D.
又∵∠BED=∠FED-∠FEB,
∴∠BED=(180°-∠D)-(180°-∠B)=∠B-∠D.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
