1.4平行线的性质(2).

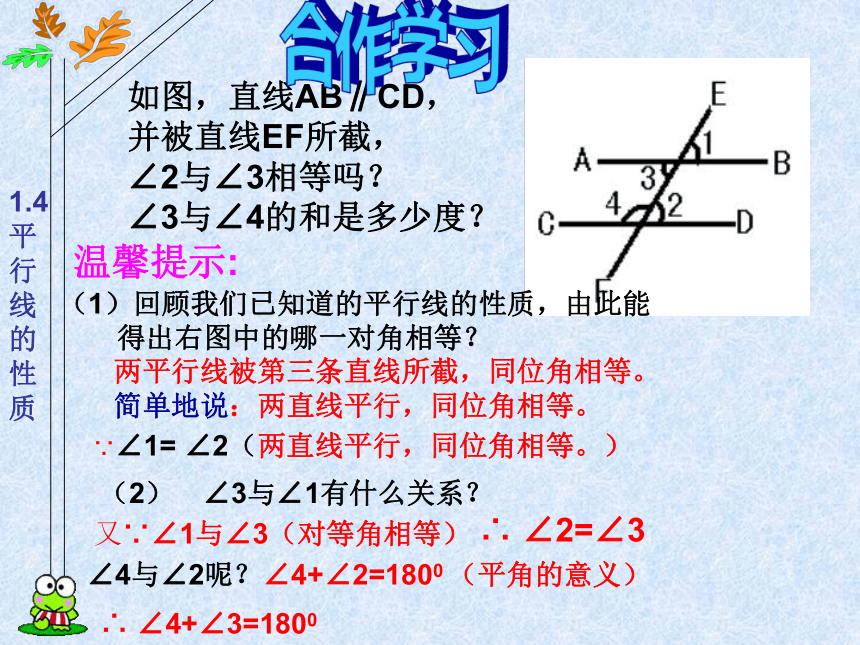
课件14张PPT。平行线的性质（2）泰顺六中 翁怀新2013年3月6日如图，直线AB∥CD，
并被直线EF所截，
∠2与∠3相等吗？
∠3与∠4的和是多少度？ 合作学习（2）　∠3与∠1有什么关系？两平行线被第三条直线所截，同位角相等。
简单地说：两直线平行，同位角相等。又∵∠1与∠3（对等角相等）∵∠1= ∠2（两直线平行，同位角相等。）（1）回顾我们已知道的平行线的性质，由此能
　　得出右图中的哪一对角相等？∴ ∠2=∠3∠4与∠2呢？∠4+∠2=1800 （平角的意义）∴ ∠4+∠3=1800 表 述 为:如图，AB，CD被EF所截，
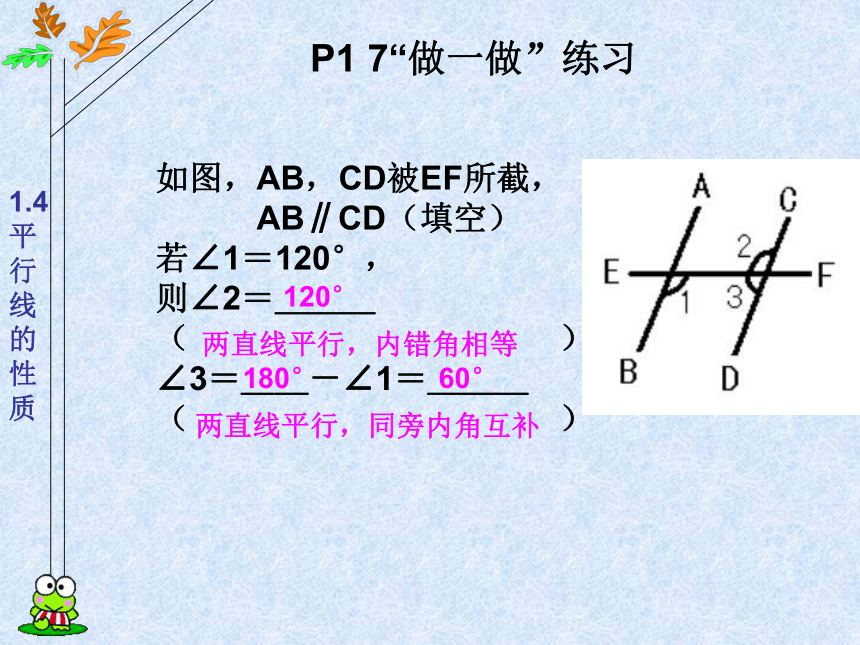
　　　AB∥CD（填空）
若∠1＝120°，
则∠2＝＿＿＿
（　　　　　　　　　　　）
∠3＝＿＿－∠1＝＿＿＿
（　　　　　　　　　　　）P1 7“做一做”练习180° 120° 60° 两直线平行，内错角相等 两直线平行，同旁内角互补 例3　
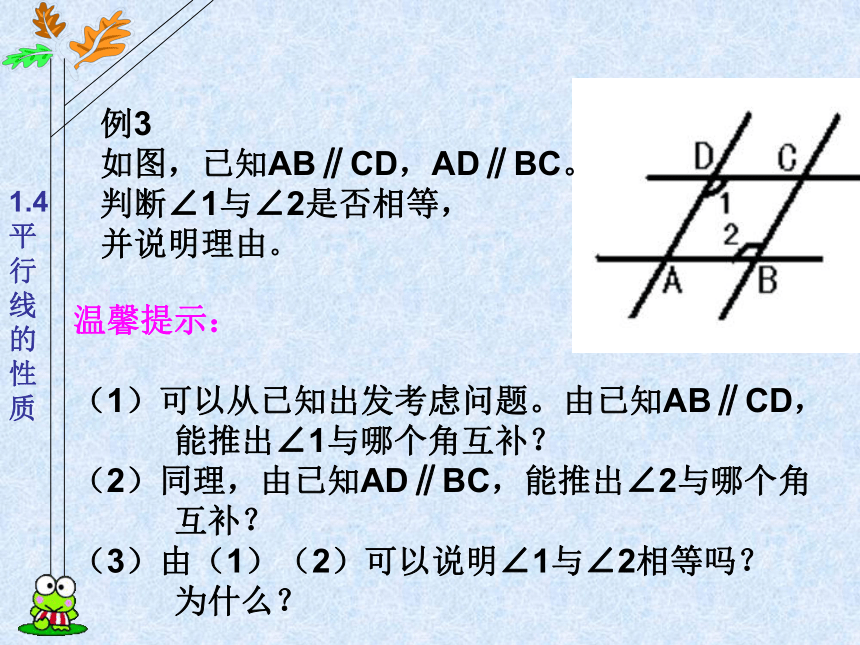
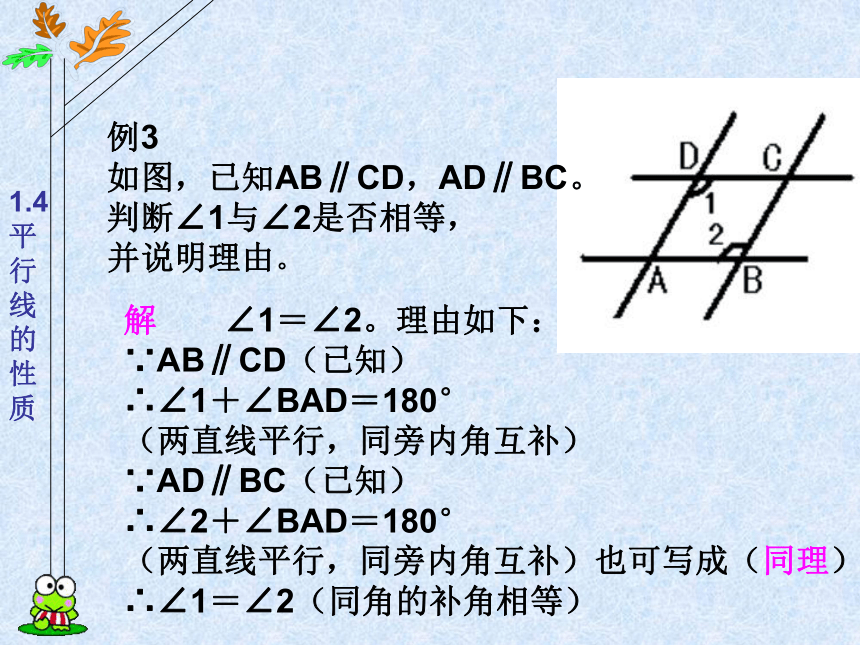
如图，已知AB∥CD，AD∥BC。
判断∠1与∠2是否相等，
并说明理由。温馨提示：
（1）可以从已知出发考虑问题。由已知AB∥CD，
　　　能推出∠1与哪个角互补？
（2）同理，由已知AD∥BC，能推出∠2与哪个角
　　　互补？
（3）由（1）（2）可以说明∠1与∠2相等吗？
　　　为什么？例3　
如图，已知AB∥CD，AD∥BC。
判断∠1与∠2是否相等，
并说明理由。解　　∠1＝∠2。理由如下：
∵AB∥CD（已知）
∴∠1＋∠BAD＝180°
（两直线平行，同旁内角互补）
∵AD∥BC（已知）
∴∠2＋∠BAD＝180°
（两直线平行，同旁内角互补）也可写成（同理）
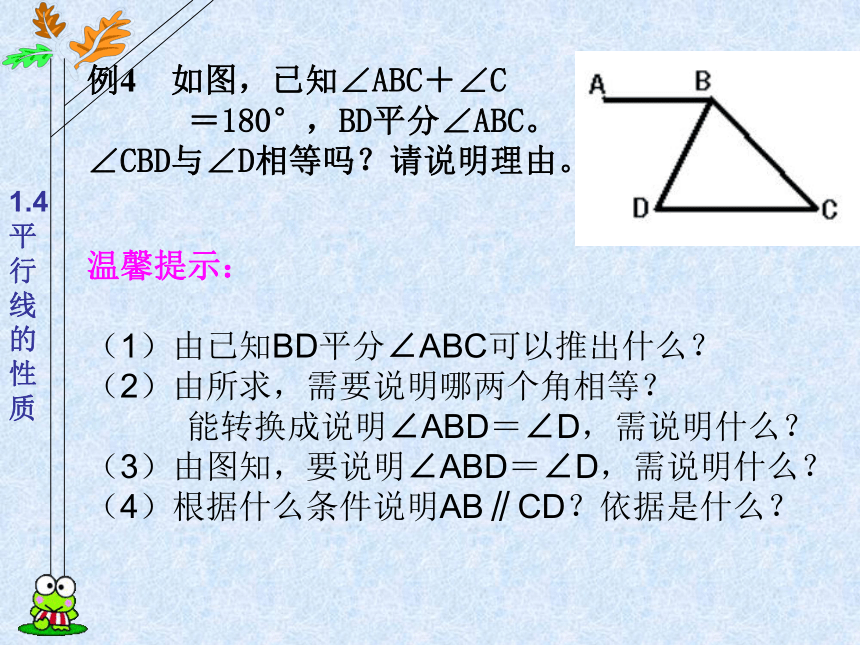
∴∠1＝∠2（同角的补角相等）例4　如图，已知∠ABC＋∠C
　　　＝180°，BD平分∠ABC。
∠CBD与∠D相等吗？请说明理由。温馨提示：
（1）由已知BD平分∠ABC可以推出什么？
（2）由所求，需要说明哪两个角相等？
　　　能转换成说明∠ABD＝∠D，需说明什么？
（3）由图知，要说明∠ABD＝∠D，需说明什么？
（4）根据什么条件说明AB∥CD？依据是什么？又∵BD平分∠ABC（已知）例4　如图，已知∠ABC＋∠C
　　　＝180°，BD平分∠ABC。
∠CBD与∠D相等吗？请说明理由。∴∠CBD＝∠D。(等量代换）解:　∠CBD＝∠D。理由如下：∵∠ABC＋∠C＝180°（已知）∴AB∥CD（同旁内角互补，两直线平行）∴∠D＝∠ABD　（两直线平行，内错角相等）（1）两直线平行，能得出什么结论？
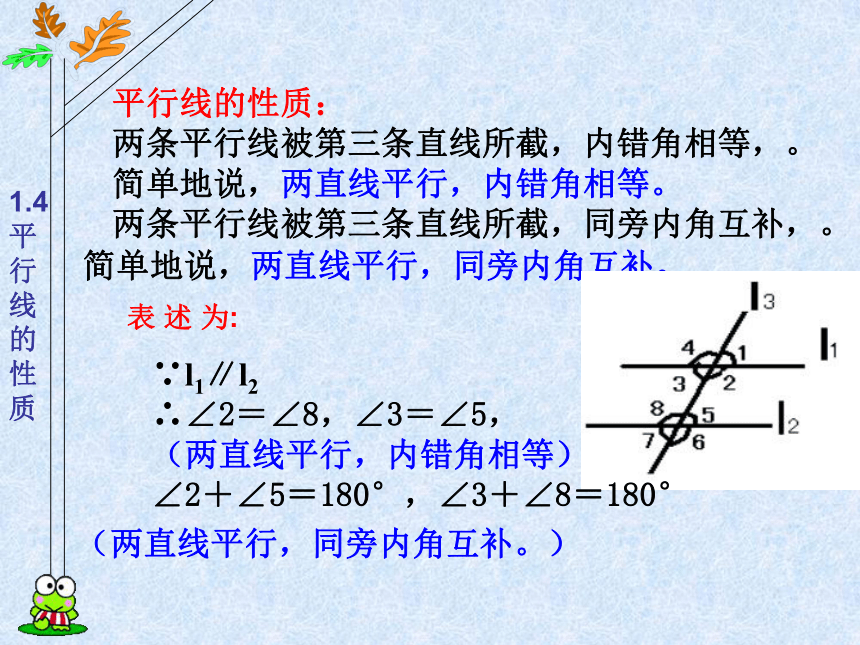
（2）有哪些条件可以得出两直线是平行的呢？ 课堂小结两条平行线被第三条直线所截，内错角相等。
简单地说，两直线平行，内错角相等。两条平行线被第三条直线所截，同旁内角互补。
简单地说，两直线平行，同旁内角互补。平行线的性质：上节课学过的平行线的性质是：两条平行线被第三条直线所截，同位角相等。
简单地说，两直线平行，同位角相等。课内练习P18课内练习：
T1　，T2　，T3课内练习1、如图：在墙面上安装一管道需经两次拐弯，拐弯后的管道与拐弯前的管道平行。若第一个弯道处∠B＝142o，那么第二个弯道处∠C为多少度?为什么?CBA∠D∠ACB两直线平行，内错角相等。3、如图：已知∠1＝∠2，∠3＝65o ，求∠4的度数?作业：
1、作业本（1）P3-4
2、课时训练P8-10再见