1.3 平行线的判定 课件(共33张PPT)
文档属性
| 名称 | 1.3 平行线的判定 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-28 17:15:10 | ||
图片预览







文档简介
(共33张PPT)
1.3 平行线的判定
数学(浙教版)
七年级 下册
第1章 平行线
学习目标
1.掌握平行线的三种判定方法,学会利用同位角、内错角和同旁内角来判定直线的平行关系;
2.学会利用平行线的判定方法进行简单的推理证明;
3.掌握垂直于同一直线的两条直线互相垂直的概念,并灵活运用来证明平行关系;
当堂检测
各抒己见:如何画平行线
已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行.
画法
1. 任意画一条直线L, 使L直线与AB垂直
2. 过点P画直线PQ和L垂直.
则PQ//AB,PQ就是所求画的直线
A
B
P
L
Q
90°
90°
导入新课
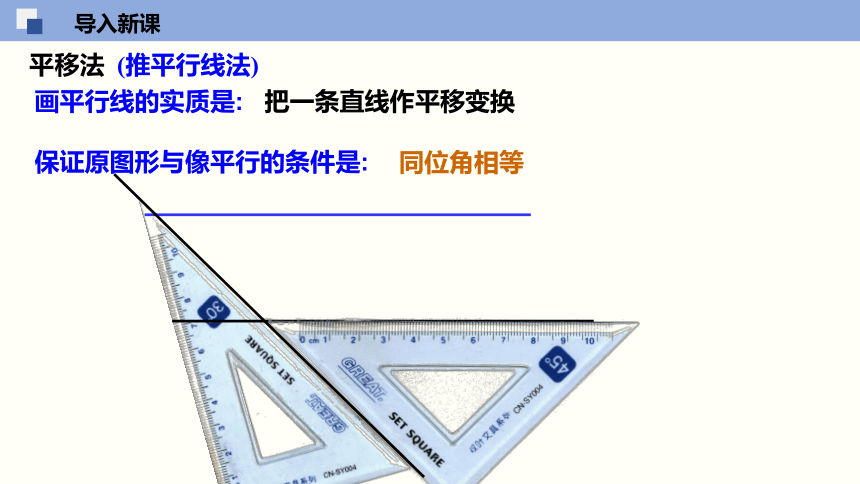
画平行线的实质是: 把一条直线作平移变换
保证原图形与像平行的条件是:
同位角相等
平移法 (推平行线法)
讲授新课
知识点一 同位角相等,两直线平行
b
A
2
1
a
B
(1)刚才的推平行线法可以看作是怎样的图形变换?
(2)在画图过程中,有没有始终相等的角?
(3)直线a,b位置关系如何?
思考
讲授新课
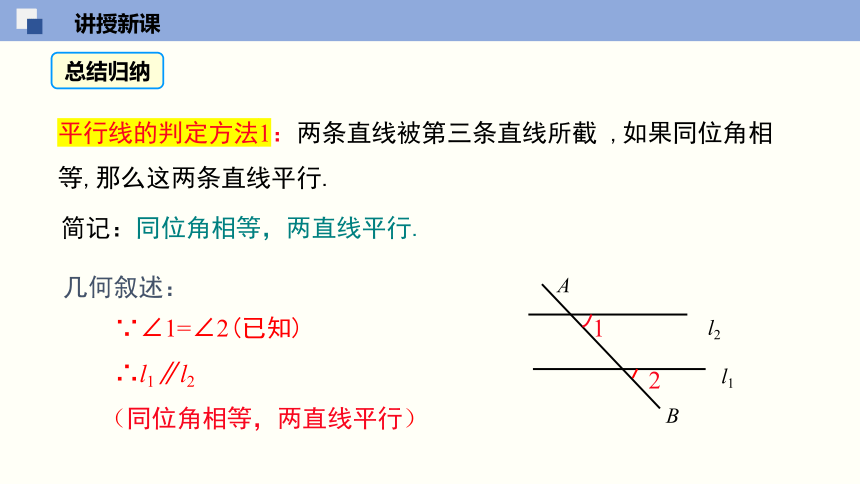
平行线的判定方法1:两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
简记:同位角相等,两直线平行.
几何叙述:
∵∠1=∠2(已知)
∴l1∥l2
(同位角相等,两直线平行)
1
2
l2
l1
A
B
总结归纳
讲授新课
典例精析
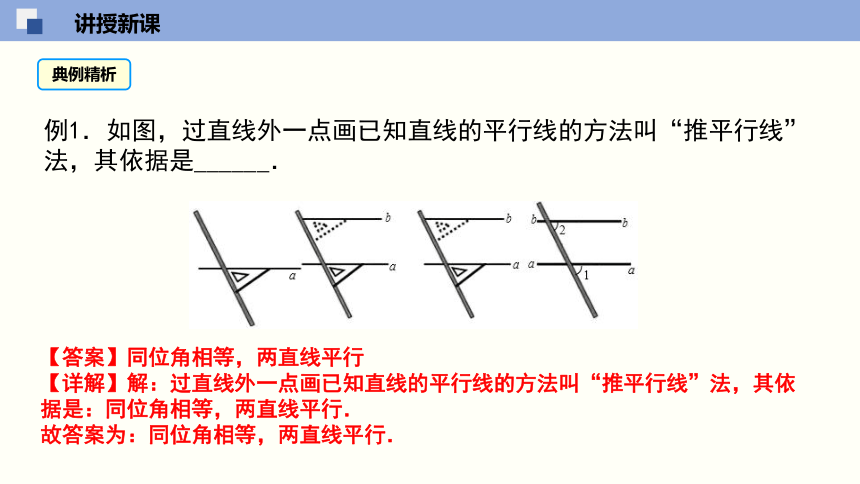
例1.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是______.
【答案】同位角相等,两直线平行
【详解】解:过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
讲授新课
练一练
1.同学们准备借助一副三角板画平行线.先画一条直线,再按如图所示的样子放置三角板.小颖认为AC∥DF,小静认为BC∥EF.你认为______的判断是正确的,依据是______.
讲授新课
【答案】 小静; 同位角相等,两条直线平行.
【分析】利用同位角相等,两条直线平行进行判断.
【详解】解:小静的判断正确.
理由如下:∵∠ABC=∠DEF=90°,
∴BC∥EF,
∵∠BAC=30°,∠EDF=45°,
∴AC与DF不平行,
∴小静的判断正确.
故答案为:小静;同位角相等,两条直线平行.
讲授新课
知识点二 内错角相等,两直线平行
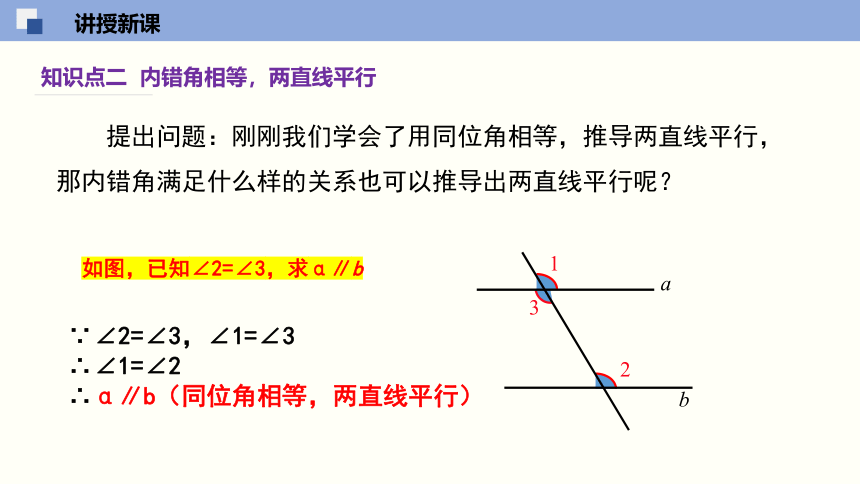
提出问题:刚刚我们学会了用同位角相等,推导两直线平行,那内错角满足什么样的关系也可以推导出两直线平行呢?
2
b
a
1
3
如图,已知∠2=∠3,求α∥b
∵∠2=∠3,∠1=∠3
∴∠1=∠2
∴α∥b(同位角相等,两直线平行)
讲授新课
平行线的判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简记:内错角相等,两直线平行.
几何叙述:
∵∠2=∠3(已知)
∴l1∥l2
(内错角相等,两直线平行)
总结归纳
2
l2
l1
1
3
讲授新课
典例精析
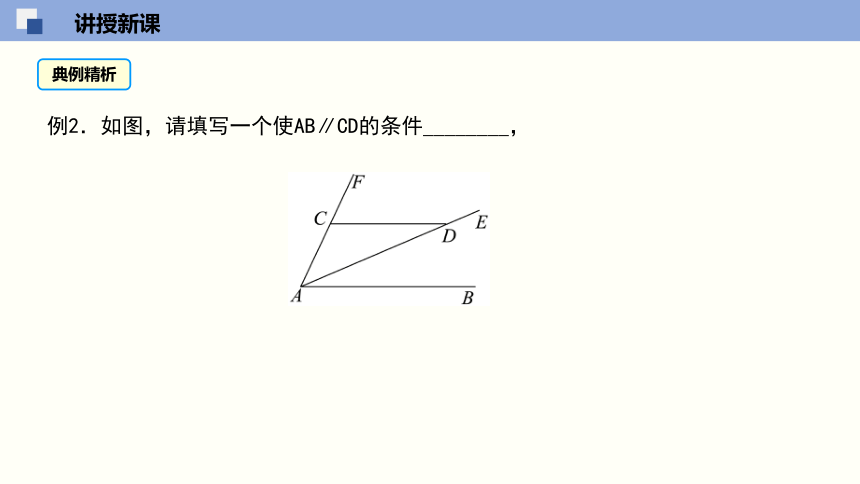
例2.如图,请填写一个使AB∥CD的条件________,
讲授新课
【答案】∠BAE=∠ADC 答案不唯一,
【分析】根据平行线的判定定理进行解答即可,
【详解】解:填写的条件为:∠BAE=∠ADC,
∵BAE=∠ADC,
∴AB∥CD(内错角相等,两直线平行),
故答案为:∠BAE=∠ADC 答案不唯一,
讲授新课
练一练
1.如图所示,请添加一个条件,使AD∥BC,可添加的条件是______.(只填一个即可)
【答案】∠2=∠4(答案不唯一)
【分析】根据平行线的判定解答即可.
【详解】解:当∠2=∠4时,AD∥BC,
故答案为:∠2=∠4(答案不唯一)
讲授新课
知识点三 同旁内角互补,两直线平行
如图,如果 1+ 2=180° 能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知)
1+ 3=180°(邻补角定义)
2= 3(同角的补角相等)
a//b (同位角相等,两直线平行)
2
b
a
1
3
讲授新课
平行线的判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简记:同旁内角互补相等,两直线平行.
几何叙述:
总结归纳
2
l2
l1
1
3
∵∠1+∠2=180°(已知)
∴l1∥l2
(同旁内角互补,两直线平行)
讲授新课
典例精析
例3.如图,因为∠1+∠2=180°(已知),因为∠3=∠1,∠2=∠4( ),所以∠3+∠4=180°,所以AB∥CD( ).
【答案】 对顶角相等 同旁内角互补两直线平行
【详解】解:因为∠1+∠2=180°(已知),
因为∠3=∠1,∠4=∠2(对顶角相等),
所以∠3+∠4=180°,
所以AB∥CD(同旁内角互补两直线平行).
讲授新课
练一练
1.如图,在下列给出的条件中,可以判定AB∥CD的有___________.
①∠1=∠2;②∠1=∠3;③∠2=∠4;④∠DAB+∠ABC=180°;⑤∠BAD+∠ADC=180°.
讲授新课
【详解】解;由∠1=∠2,不可以证明AB∥CD,故①错误;
由∠1=∠3,可以证明AB∥CD(内错角相等,两直线平行),故②正确;
由∠2=∠4,可以证明AB∥CD(内错角相等,两直线平行),故③正确;
由∠DAB+∠ABC=180°,不可以证明AB∥CD,故④错误;
由∠BAD+∠ADC=180°,可以证明AB∥CD(同旁内角互补,两直线平行),故⑤正确;
故答案为;②③⑤.
讲授新课
知识点四 垂直于同一直线的两条直线互相平行
思考:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
a
b
c
1
2
垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
你还能利用其他方法说明b//c吗?
思考:为什么要加“在同一平面内”这个条件?
讲授新课
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:如图,
讲授新课
垂直于同一条直线的两条直线平行.
几何叙述:
∵ b⊥a,c⊥a(已知)
∴b∥c(垂直于同一条直线的两条直线平行.)
a
b
c
1
2
归纳总结
讲授新课
典例精析
例4.如图, a⊥c,b⊥c,则直线a、b的关系是________
【详解】解:由图可知,两直线在同一平面内,
又∵a⊥c,b⊥c,
∴a∥b,
故答案为:a∥b.
讲授新课
练一练
1.如图,小红看到工人师傅用角尺画出工件边缘AB的垂线α和b,即可得到α∥b.请你帮小红从下列真命题中找到工人师傅画图的一个依据.真命题为:①连接直线外一点与直线上各点的所有线段中,垂线段最短;②在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行(选自人教版初中数学教科书七年级下册第14页例);③在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线;④经过直线外一点,有且只有一条直线与这条直线平行.”这个依据是__________.(只需填序号)
讲授新课
【详解】解:由题意:a⊥AB,b⊥AB,
∴α∥b(在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行),
故答案为:②.
当堂检测
1.如图下列不能判定AB∥CD的条件是( )
A.∠B+∠BCD=180° B.∠1=∠4
C.∠3=∠2 D.∠B=∠5
C、∵∠3=∠2,
∴AD∥BC(内错角相等,两直线平行)
∴本选项符合题意;
【分析】根据平行线的判定定理对选项进行逐一判断即可.
当堂检测
2.在下列说法中,正确的有( )
①两点确定一条直线;
②过一点有且只有一条直线与已知直线平行;
③垂直于同一条直线的两条直线垂直;
④平行于同一条直线的两条直线平行;
⑤过一点有且只有一条直线和已知直线垂直.
A.1个 B.2个 C.3个 D.4个
当堂检测
【详解】解:①两点确定一条直线,正确;
②应为过直线外一点有且只有一条直线与已知直线平行,故本小题错误;
③应为在同一平面内,垂直于同一条直线的两条直线平行,故本小题错误;
④平行于同一条直线的两条直线平行,正确;
⑤应为在同一个平面内,过一点有且只有一条直线和已知直线垂直,故本小题错误;
综上所述,说法正确的有①④共2个.
故选B.
当堂检测
3.如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这两条直线的位置关系是 ____,这是因为 ____.
【答案】 平行 同旁内角互补,两直线平行
【详解】解:一组同旁内角的度数比为3:2,差为36°
∴设较小的角为:x,则较大的为x+36°
∴(x+36°):x=3:2
∴x=72°,x+36°=108°
∵72°+108°=180°即同旁内角互补.
∴这两条直线的位置关系是平行
∴答案为:平行,同旁内角互补,两直线平行.
当堂检测
4.如图,把三角尺的直角顶点放在直线b上.若∠1= 50°,则当∠2=____时,a∥b.
【详解】解:如图,
∵三角尺的直角顶点在直线b上,∠1=20°,
∴∠3=180° 90° ∠1=40°,
又∵要使得a∥b,
∴只需要∠2=∠3=40°,
故答案为:40.
当堂检测
5.如图,AC与AB、CD相交于点A、C,AE平分∠CAB交CD于点E,∠ACD=40°,∠BAE=70°.试判断直线AB与CD的位置关系,并说明理由.
【详解】解:AB∥CD,理由如下:
∵AE平分∠CAB,∠BAE=70°,
∴∠BAC=2∠BAE=2×70°=140°,
∵∠ACD=40°,
∴∠BAC+∠ACD=140°+40°=180°,
∴AB∥CD.
课堂小结
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知) ∴a∥b
________相等 两直线平行 ∵ (已知) ∴a∥b _________互补 两直线平行 ∵ (已知) ∴a∥b 谢 谢~
1.3 平行线的判定
数学(浙教版)
七年级 下册
第1章 平行线
学习目标
1.掌握平行线的三种判定方法,学会利用同位角、内错角和同旁内角来判定直线的平行关系;
2.学会利用平行线的判定方法进行简单的推理证明;
3.掌握垂直于同一直线的两条直线互相垂直的概念,并灵活运用来证明平行关系;
当堂检测
各抒己见:如何画平行线
已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行.
画法
1. 任意画一条直线L, 使L直线与AB垂直
2. 过点P画直线PQ和L垂直.
则PQ//AB,PQ就是所求画的直线
A
B
P
L
Q
90°
90°
导入新课
画平行线的实质是: 把一条直线作平移变换
保证原图形与像平行的条件是:
同位角相等
平移法 (推平行线法)
讲授新课
知识点一 同位角相等,两直线平行
b
A
2
1
a
B
(1)刚才的推平行线法可以看作是怎样的图形变换?
(2)在画图过程中,有没有始终相等的角?
(3)直线a,b位置关系如何?
思考
讲授新课
平行线的判定方法1:两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
简记:同位角相等,两直线平行.
几何叙述:
∵∠1=∠2(已知)
∴l1∥l2
(同位角相等,两直线平行)
1
2
l2
l1
A
B
总结归纳
讲授新课
典例精析
例1.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是______.
【答案】同位角相等,两直线平行
【详解】解:过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
讲授新课
练一练
1.同学们准备借助一副三角板画平行线.先画一条直线,再按如图所示的样子放置三角板.小颖认为AC∥DF,小静认为BC∥EF.你认为______的判断是正确的,依据是______.
讲授新课
【答案】 小静; 同位角相等,两条直线平行.
【分析】利用同位角相等,两条直线平行进行判断.
【详解】解:小静的判断正确.
理由如下:∵∠ABC=∠DEF=90°,
∴BC∥EF,
∵∠BAC=30°,∠EDF=45°,
∴AC与DF不平行,
∴小静的判断正确.
故答案为:小静;同位角相等,两条直线平行.
讲授新课
知识点二 内错角相等,两直线平行
提出问题:刚刚我们学会了用同位角相等,推导两直线平行,那内错角满足什么样的关系也可以推导出两直线平行呢?
2
b
a
1
3
如图,已知∠2=∠3,求α∥b
∵∠2=∠3,∠1=∠3
∴∠1=∠2
∴α∥b(同位角相等,两直线平行)
讲授新课
平行线的判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简记:内错角相等,两直线平行.
几何叙述:
∵∠2=∠3(已知)
∴l1∥l2
(内错角相等,两直线平行)
总结归纳
2
l2
l1
1
3
讲授新课
典例精析
例2.如图,请填写一个使AB∥CD的条件________,
讲授新课
【答案】∠BAE=∠ADC 答案不唯一,
【分析】根据平行线的判定定理进行解答即可,
【详解】解:填写的条件为:∠BAE=∠ADC,
∵BAE=∠ADC,
∴AB∥CD(内错角相等,两直线平行),
故答案为:∠BAE=∠ADC 答案不唯一,
讲授新课
练一练
1.如图所示,请添加一个条件,使AD∥BC,可添加的条件是______.(只填一个即可)
【答案】∠2=∠4(答案不唯一)
【分析】根据平行线的判定解答即可.
【详解】解:当∠2=∠4时,AD∥BC,
故答案为:∠2=∠4(答案不唯一)
讲授新课
知识点三 同旁内角互补,两直线平行
如图,如果 1+ 2=180° 能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知)
1+ 3=180°(邻补角定义)
2= 3(同角的补角相等)
a//b (同位角相等,两直线平行)
2
b
a
1
3
讲授新课
平行线的判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简记:同旁内角互补相等,两直线平行.
几何叙述:
总结归纳
2
l2
l1
1
3
∵∠1+∠2=180°(已知)
∴l1∥l2
(同旁内角互补,两直线平行)
讲授新课
典例精析
例3.如图,因为∠1+∠2=180°(已知),因为∠3=∠1,∠2=∠4( ),所以∠3+∠4=180°,所以AB∥CD( ).
【答案】 对顶角相等 同旁内角互补两直线平行
【详解】解:因为∠1+∠2=180°(已知),
因为∠3=∠1,∠4=∠2(对顶角相等),
所以∠3+∠4=180°,
所以AB∥CD(同旁内角互补两直线平行).
讲授新课
练一练
1.如图,在下列给出的条件中,可以判定AB∥CD的有___________.
①∠1=∠2;②∠1=∠3;③∠2=∠4;④∠DAB+∠ABC=180°;⑤∠BAD+∠ADC=180°.
讲授新课
【详解】解;由∠1=∠2,不可以证明AB∥CD,故①错误;
由∠1=∠3,可以证明AB∥CD(内错角相等,两直线平行),故②正确;
由∠2=∠4,可以证明AB∥CD(内错角相等,两直线平行),故③正确;
由∠DAB+∠ABC=180°,不可以证明AB∥CD,故④错误;
由∠BAD+∠ADC=180°,可以证明AB∥CD(同旁内角互补,两直线平行),故⑤正确;
故答案为;②③⑤.
讲授新课
知识点四 垂直于同一直线的两条直线互相平行
思考:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
a
b
c
1
2
垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
你还能利用其他方法说明b//c吗?
思考:为什么要加“在同一平面内”这个条件?
讲授新课
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:如图,
讲授新课
垂直于同一条直线的两条直线平行.
几何叙述:
∵ b⊥a,c⊥a(已知)
∴b∥c(垂直于同一条直线的两条直线平行.)
a
b
c
1
2
归纳总结
讲授新课
典例精析
例4.如图, a⊥c,b⊥c,则直线a、b的关系是________
【详解】解:由图可知,两直线在同一平面内,
又∵a⊥c,b⊥c,
∴a∥b,
故答案为:a∥b.
讲授新课
练一练
1.如图,小红看到工人师傅用角尺画出工件边缘AB的垂线α和b,即可得到α∥b.请你帮小红从下列真命题中找到工人师傅画图的一个依据.真命题为:①连接直线外一点与直线上各点的所有线段中,垂线段最短;②在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行(选自人教版初中数学教科书七年级下册第14页例);③在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线;④经过直线外一点,有且只有一条直线与这条直线平行.”这个依据是__________.(只需填序号)
讲授新课
【详解】解:由题意:a⊥AB,b⊥AB,
∴α∥b(在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行),
故答案为:②.
当堂检测
1.如图下列不能判定AB∥CD的条件是( )
A.∠B+∠BCD=180° B.∠1=∠4
C.∠3=∠2 D.∠B=∠5
C、∵∠3=∠2,
∴AD∥BC(内错角相等,两直线平行)
∴本选项符合题意;
【分析】根据平行线的判定定理对选项进行逐一判断即可.
当堂检测
2.在下列说法中,正确的有( )
①两点确定一条直线;
②过一点有且只有一条直线与已知直线平行;
③垂直于同一条直线的两条直线垂直;
④平行于同一条直线的两条直线平行;
⑤过一点有且只有一条直线和已知直线垂直.
A.1个 B.2个 C.3个 D.4个
当堂检测
【详解】解:①两点确定一条直线,正确;
②应为过直线外一点有且只有一条直线与已知直线平行,故本小题错误;
③应为在同一平面内,垂直于同一条直线的两条直线平行,故本小题错误;
④平行于同一条直线的两条直线平行,正确;
⑤应为在同一个平面内,过一点有且只有一条直线和已知直线垂直,故本小题错误;
综上所述,说法正确的有①④共2个.
故选B.
当堂检测
3.如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这两条直线的位置关系是 ____,这是因为 ____.
【答案】 平行 同旁内角互补,两直线平行
【详解】解:一组同旁内角的度数比为3:2,差为36°
∴设较小的角为:x,则较大的为x+36°
∴(x+36°):x=3:2
∴x=72°,x+36°=108°
∵72°+108°=180°即同旁内角互补.
∴这两条直线的位置关系是平行
∴答案为:平行,同旁内角互补,两直线平行.
当堂检测
4.如图,把三角尺的直角顶点放在直线b上.若∠1= 50°,则当∠2=____时,a∥b.
【详解】解:如图,
∵三角尺的直角顶点在直线b上,∠1=20°,
∴∠3=180° 90° ∠1=40°,
又∵要使得a∥b,
∴只需要∠2=∠3=40°,
故答案为:40.
当堂检测
5.如图,AC与AB、CD相交于点A、C,AE平分∠CAB交CD于点E,∠ACD=40°,∠BAE=70°.试判断直线AB与CD的位置关系,并说明理由.
【详解】解:AB∥CD,理由如下:
∵AE平分∠CAB,∠BAE=70°,
∴∠BAC=2∠BAE=2×70°=140°,
∵∠ACD=40°,
∴∠BAC+∠ACD=140°+40°=180°,
∴AB∥CD.
课堂小结
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知) ∴a∥b
________相等 两直线平行 ∵ (已知) ∴a∥b _________互补 两直线平行 ∵ (已知) ∴a∥b 谢 谢~
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
