1.5 图形的平移 课件(共25张PPT)
文档属性
| 名称 | 1.5 图形的平移 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览





文档简介
图
形
的
平
移
授 课 人 :
01. 掌握平行线的性质.
02. 掌握分析问题的方法,提高解题能力.
03. 能用平行线的性质和判定进行简单的推理和计算.
目
标
情境导入
下面两个图形的变换各是什么变换?请说明理由。
轴对称变换:原图形和它的像能关于它们之间的一条竖向的直线对称.
平移变换:所有的点都沿同一方向运动了相等的距离.
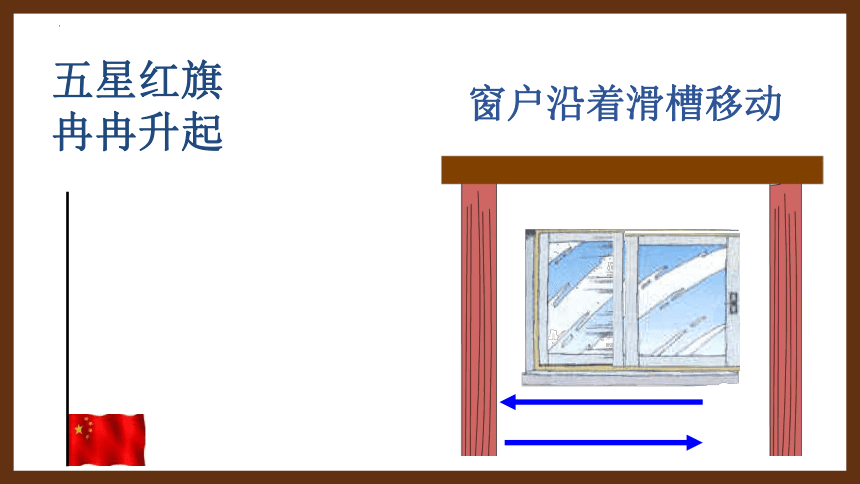
五星红旗冉冉升起
窗户沿着滑槽移动
飞机在天空飞行
上述这些运动现象都给我们带来了怎样一种感觉?
探究新知
知识点一:平移的概念
观察上面几组美丽的图案,它们有什么共同的特点?能否根据每幅图中的一部分绘制出整幅图案?
探究新知
思 考
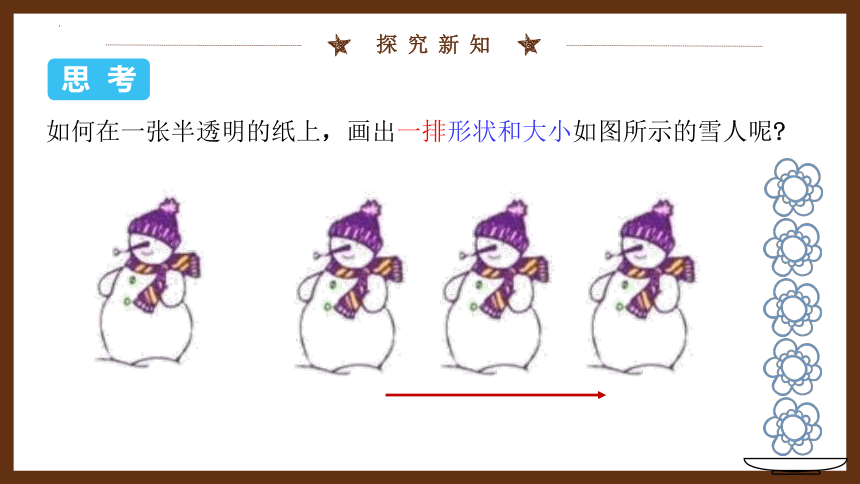
如何在一张半透明的纸上,画出一排形状和大小如图所示的雪人呢?
总结归纳
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如下图).
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移的要素:1.移动的方向;
2.移动的距离
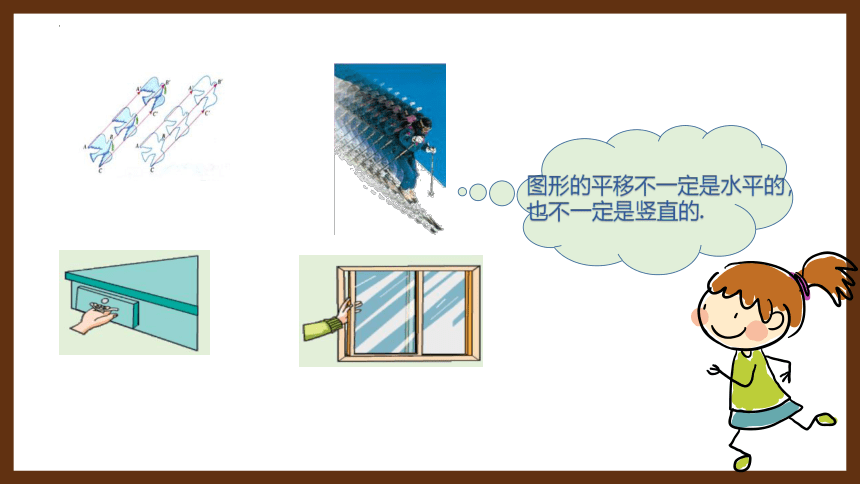
图形的平移不一定是水平的,
也不一定是竖直的.
典例精讲
例1 以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
D
探究新知
知识点二:平移的性质
思 考
如图,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A',帽顶B与B',纽扣C与C'),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
A
A
'
C
C
'
B
B
'
A
B
C
D
E
F
P
Q
E
F
A
B
C
D
总结归纳
图形平移的基本性质
平移的两个图形形状和大小完全相同
②对应线段平行(或在同一直线上)且相等,对应角相等;
③各对应点所连线段平行(或在同一直线上)且相等;
例2 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,
∠CDA与∠GHE之间有什么数量关系?
典例精讲
解:(1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
例3 如图,平移三角形ABC,使点A移动到点A',画出平移后的三角形A'B'C'.
A
B
C
A?
解:如图,连接AA',过点B作AA'的平行线l,
在l上截取BB'=AA',则点B'就是点B的对应点.类似地,
作出点C的对应点C',并进一步得到平移后的三角形A'B'C' .
A
B
C
A?
B?
l
A
B
C
A?
C?
B?
l
知识点三:平移的作图
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
总结归纳
随堂演练
1.下图中的变换属于平移的有哪些?
F
A
B
D
E
C
×
×
×
√
×
×
2.下列生活中的物体的运动情况可以看成平移的是( )
A.篮球运动员投篮时篮球的运动
B.飞机在跑道上滑行到停止的运动
C.空中放飞的风筝的运动
D.冷水加热过程中小气泡上升变为大气泡
B
3. 如图,将三角形ABC平移可得到三角形A′B′C′,则图中平行线共有( )
A.3对
B.4对
C.5对
D.6对
D
4. 如图,将三角形ABC 沿直线AB向右平移后到达三角形BDE的位置.若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
50°
5. 如图,将三角形ABC沿BC方向平移至三角形DEF处.
若EC=2BE=2,则CF的长为 .
1
6.如图,经过平移,四边形ABCD的顶点A移动到点A′,
作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
7. 如图,在三角形ABC中,AC=4 cm,BC=3 cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8 cm,DB=2 cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
解:(1)∵三角形ABC沿AB方向向右平移得到三角形DEF,
∴AD=BE=CF,BC=EF=3 cm.
∵AE=8 cm,DB=2 cm,
∴AD=BE=CF= ×(8-2)=3(cm).
(2)四边形AEFC的周长 =AE+EF+CF+AC=8+3+3+4=18(cm).
拓展提高
如图,将△ABC沿BC方向平移,得到△DEF,若AB=6,BC=8,DH=3,BE=4.
(1)若∠A=53°,求∠CHE的度数。
(2)求图中阴影部分的面积。
A
B
C
D
E
F
H
解:①∵△DEF是由△ABC平移得到的
∴∠D=∠A,AC∥DF
∴∠CHE=∠D
∴∠CHE=∠A=53°
②∵△DEF是由△ABC平移得到的
∴DE=AB=6∴HE=DE - DH=4.5
∵∠B=90°
∴四边形ABEH是梯形,S阴影=S△DEF - S△CEH
=S梯形ABEH= (AB+HE)×BE
= ×(6+4.5)×4=21
12
?
12
?
课堂小结
定--找--移--连
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等,对应角相等
平移的概念
平移的性质
平移作图
平移
各对应点所连线段平行(或在同一直线上)且相等
谢
谢
形
的
平
移
授 课 人 :
01. 掌握平行线的性质.
02. 掌握分析问题的方法,提高解题能力.
03. 能用平行线的性质和判定进行简单的推理和计算.
目
标
情境导入
下面两个图形的变换各是什么变换?请说明理由。
轴对称变换:原图形和它的像能关于它们之间的一条竖向的直线对称.
平移变换:所有的点都沿同一方向运动了相等的距离.
五星红旗冉冉升起
窗户沿着滑槽移动
飞机在天空飞行
上述这些运动现象都给我们带来了怎样一种感觉?
探究新知
知识点一:平移的概念
观察上面几组美丽的图案,它们有什么共同的特点?能否根据每幅图中的一部分绘制出整幅图案?
探究新知
思 考
如何在一张半透明的纸上,画出一排形状和大小如图所示的雪人呢?
总结归纳
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如下图).
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
平移的要素:1.移动的方向;
2.移动的距离
图形的平移不一定是水平的,
也不一定是竖直的.
典例精讲
例1 以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
D
探究新知
知识点二:平移的性质
思 考
如图,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A',帽顶B与B',纽扣C与C'),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
A
A
'
C
C
'
B
B
'
A
B
C
D
E
F
P
Q
E
F
A
B
C
D
总结归纳
图形平移的基本性质
平移的两个图形形状和大小完全相同
②对应线段平行(或在同一直线上)且相等,对应角相等;
③各对应点所连线段平行(或在同一直线上)且相等;
例2 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,
∠CDA与∠GHE之间有什么数量关系?
典例精讲
解:(1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
例3 如图,平移三角形ABC,使点A移动到点A',画出平移后的三角形A'B'C'.
A
B
C
A?
解:如图,连接AA',过点B作AA'的平行线l,
在l上截取BB'=AA',则点B'就是点B的对应点.类似地,
作出点C的对应点C',并进一步得到平移后的三角形A'B'C' .
A
B
C
A?
B?
l
A
B
C
A?
C?
B?
l
知识点三:平移的作图
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
总结归纳
随堂演练
1.下图中的变换属于平移的有哪些?
F
A
B
D
E
C
×
×
×
√
×
×
2.下列生活中的物体的运动情况可以看成平移的是( )
A.篮球运动员投篮时篮球的运动
B.飞机在跑道上滑行到停止的运动
C.空中放飞的风筝的运动
D.冷水加热过程中小气泡上升变为大气泡
B
3. 如图,将三角形ABC平移可得到三角形A′B′C′,则图中平行线共有( )
A.3对
B.4对
C.5对
D.6对
D
4. 如图,将三角形ABC 沿直线AB向右平移后到达三角形BDE的位置.若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
50°
5. 如图,将三角形ABC沿BC方向平移至三角形DEF处.
若EC=2BE=2,则CF的长为 .
1
6.如图,经过平移,四边形ABCD的顶点A移动到点A′,
作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
7. 如图,在三角形ABC中,AC=4 cm,BC=3 cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8 cm,DB=2 cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
解:(1)∵三角形ABC沿AB方向向右平移得到三角形DEF,
∴AD=BE=CF,BC=EF=3 cm.
∵AE=8 cm,DB=2 cm,
∴AD=BE=CF= ×(8-2)=3(cm).
(2)四边形AEFC的周长 =AE+EF+CF+AC=8+3+3+4=18(cm).
拓展提高
如图,将△ABC沿BC方向平移,得到△DEF,若AB=6,BC=8,DH=3,BE=4.
(1)若∠A=53°,求∠CHE的度数。
(2)求图中阴影部分的面积。
A
B
C
D
E
F
H
解:①∵△DEF是由△ABC平移得到的
∴∠D=∠A,AC∥DF
∴∠CHE=∠D
∴∠CHE=∠A=53°
②∵△DEF是由△ABC平移得到的
∴DE=AB=6∴HE=DE - DH=4.5
∵∠B=90°
∴四边形ABEH是梯形,S阴影=S△DEF - S△CEH
=S梯形ABEH= (AB+HE)×BE
= ×(6+4.5)×4=21
12
?
12
?
课堂小结
定--找--移--连
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等,对应角相等
平移的概念
平移的性质
平移作图
平移
各对应点所连线段平行(或在同一直线上)且相等
谢
谢
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
