浙教版(2012)七年级数学下册 第1章平行线单元测试卷(含解析)
文档属性
| 名称 | 浙教版(2012)七年级数学下册 第1章平行线单元测试卷(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 18:48:26 | ||
图片预览


文档简介
浙教版(2012)七年级数学下册单元测试卷
第1章 平 行 线
时间:100分 总分120分
一、选择题(每题3分,共24分)
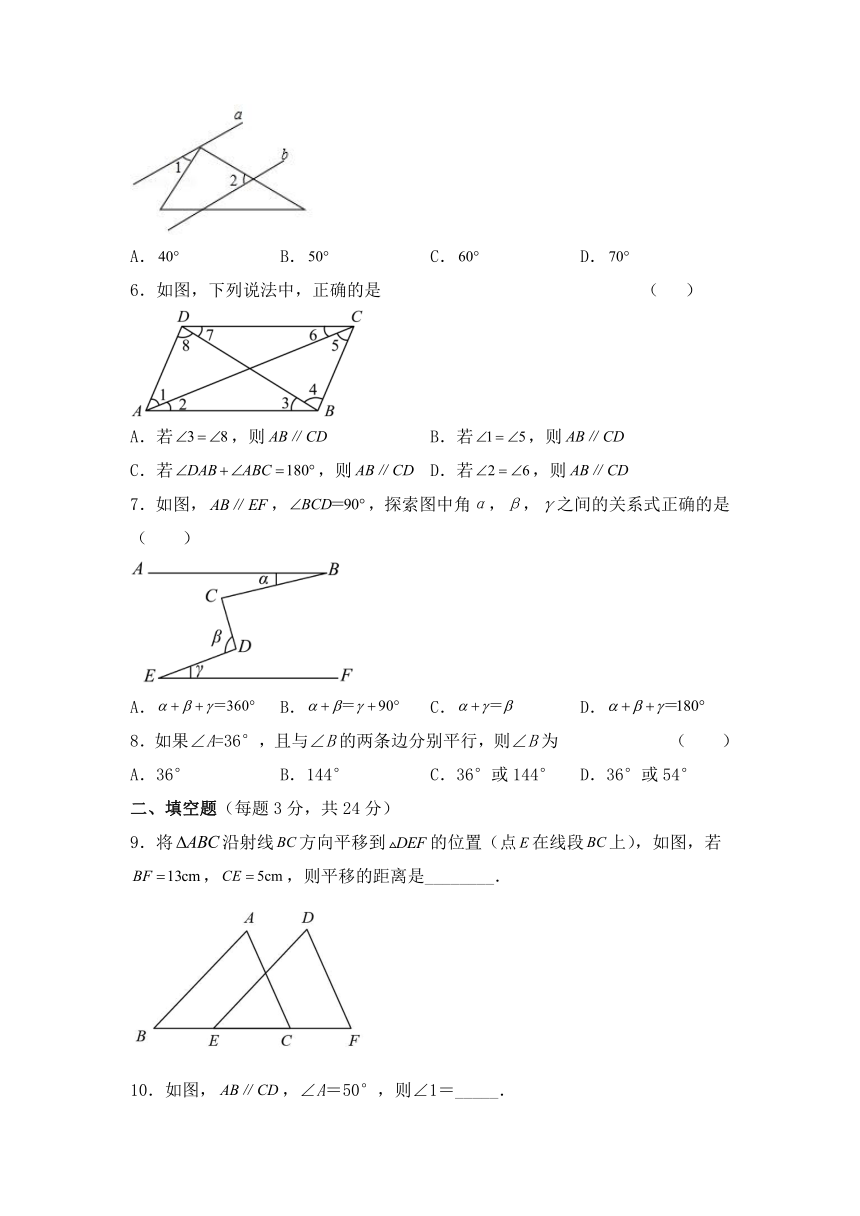
1.以下运动属于平移运动的是 ( )
A.彩旗飘飘 B.荡秋千 C.电梯升降 D.折纸
2.图中与是同位角的有 ( )
A.1个 B.2个 C.3个 D.4个
3.下列图形中,根据AB∥CD,能得到的是 ( )
A. B.
C. D.
4.如图,是的平分线,,若,则的度数为( )
A.17.5° B.35° C.55° D.70°
5.如图,已知a∥b,直角三角板的直角顶点在直线 a 上,若,则等于 ( )
A. B. C. D.
6.如图,下列说法中,正确的是 ( )
A.若,则 B.若,则
C.若,则 D.若,则
7.如图,,,探索图中角α,β,γ之间的关系式正确的是 ( )
A. B. C. D.
8.如果∠A=36°,且与∠B的两条边分别平行,则∠B为 ( )
A.36° B.144° C.36°或144° D.36°或54°
二、填空题(每题3分,共24分)
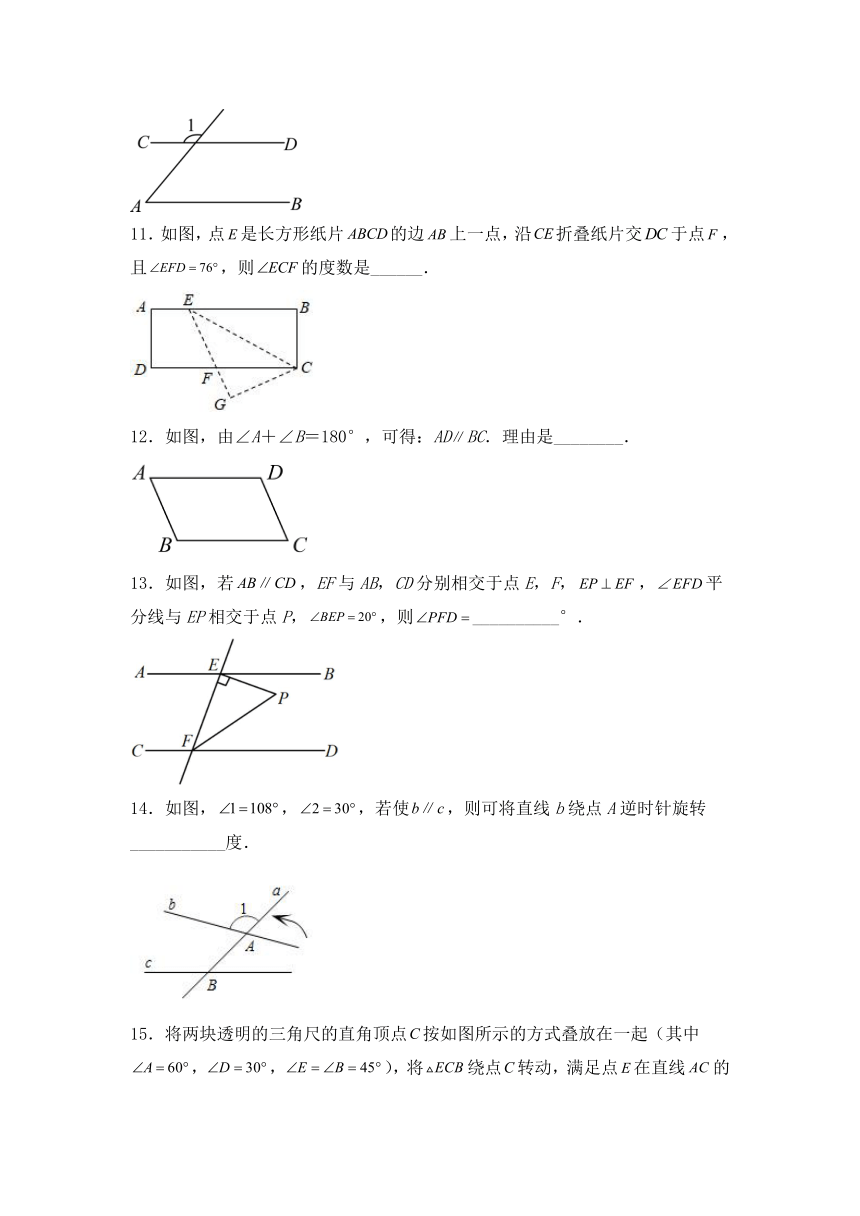
9.将沿射线方向平移到的位置(点在线段上),如图,若,,则平移的距离是________.
10.如图,,∠A=50°,则∠1=_____.
11.如图,点是长方形纸片的边上一点,沿折叠纸片交于点,且,则的度数是______.
12.如图,由∠A+∠B=180°,可得:ADBC.理由是________.
13.如图,若,EF与AB,CD分别相交于点E,F,,平分线与EP相交于点P,,则__________°.
14.如图,,,若使,则可将直线b绕点A逆时针旋转___________度.
15.将两块透明的三角尺的直角顶点按如图所示的方式叠放在一起(其中,,),将绕点转动,满足点在直线的上方,且小于,当这两块三角尺有一组边互相平行时,的度数为______.
16.沈阳市政府拟定在中央公园建设大型灯光秀,在某平行湖道两岸所在直线、安装探照灯,若灯P发出的光束自逆时针旋转至便立即回转,灯Q发出的光束自逆时针旋转至便立即回转,每天晚间两灯同时开启不停交叉照射巡视.设灯P光束转动的速度是10度/秒,灯Q光束转动的速度是4度/秒,在两灯同时开启后的35秒内,开启______秒时,两灯的光束互相垂直.
三、解答题(每题8分,共72分)
17.如图,网格中每个小正方形的边长均为1,点、、均在小正方形的顶点,把三角形平移得到三角形,使点的对应点为.
(1)请在图中画出三角形.
(2)连接、,直接写出三角形的面积为___________.
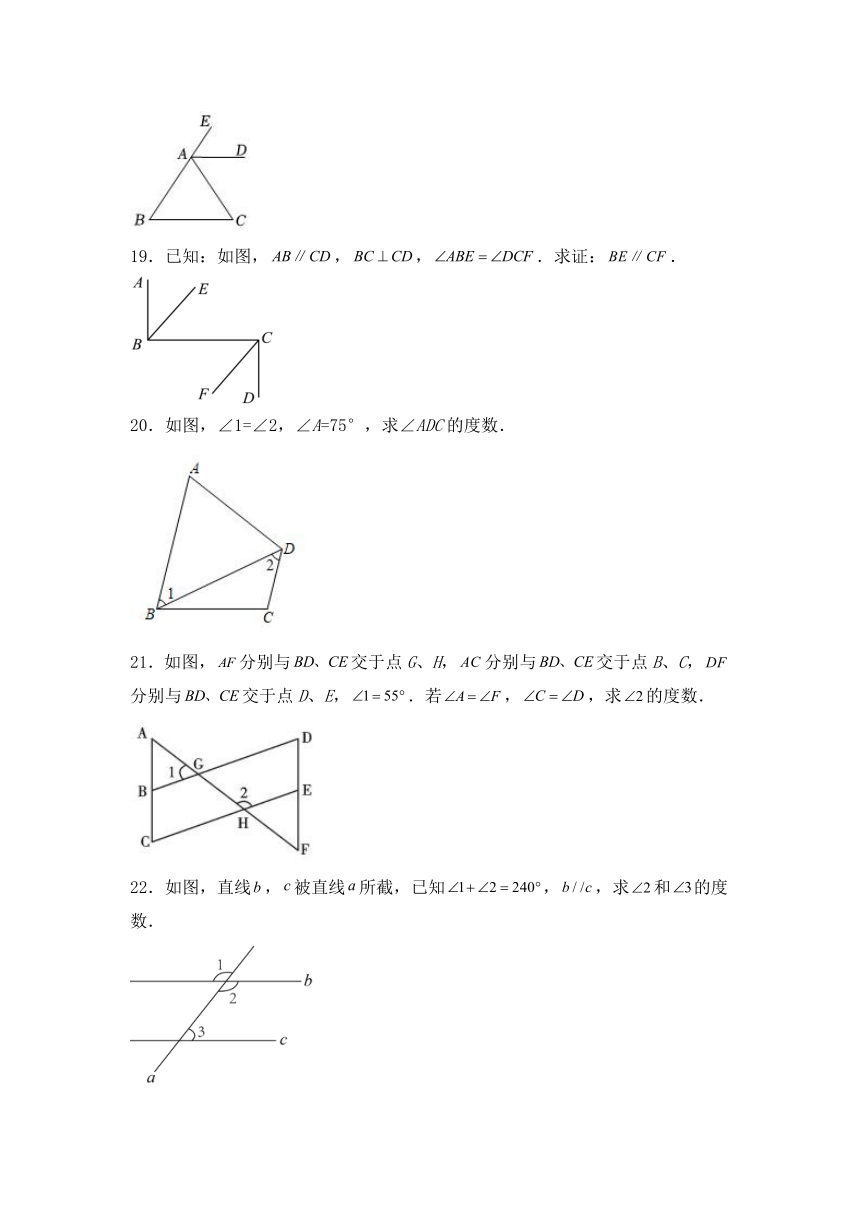
18.如图所示,已知∠B=∠C=∠DAC,求证:AD平分∠CAE.
19.已知:如图,,,.求证:.
20.如图,∠1=∠2,∠A=75°,求∠ADC的度数.
21.如图,分别与交于点G、H,分别与交于点B、C,分别与交于点D、E,.若,,求的度数.
22.如图,直线,被直线所截,已知,,求和的度数.
23.如图,E在四边形的边的延长线上,连接BE交AD于F,已知,,求证:AB∥CD.
24.如图,E是线段上一点,与平行吗?为什么?
25.长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即,连结,且.灯射线自顺时针旋转至便立即回转,灯射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是1度/秒,灯转动的速度是3度/秒.
(1)若两灯同时转动,在灯射线第一次转到之前,两灯射出的光线交于点.
①如图1,当两灯光线同时转动50秒时,求的度数.
②如图2,过作交于点,则在转动过程中,求与的比值,并说明理由.
(2)若灯射线先转动30秒,灯射线才开始转动,在灯射线第一次转到之前,灯转动几秒,两灯的光线互相平行?
参考答案:
1.
【解析】解:A、不属于平移,故此选项错误;
B、属于旋转,故此选项错误;
C、属于平移,故此选项正确;
D、属于翻折变换,故此选项错误;
故选:C.
2.
【解析】解:第1个图和第4个图中的与是同位角,有2个,
故选:B.
3.
【解析】解:A.∵,
∴,
故选项不符合题意;
B.∵,
∴,得不到,
故选项不符合题意;
C.如图,
∵,
∴,
∵,
∴,
故选项正确,符合题意;
D.由得不到,故选项不符合题意.
故选:C.
4.
【解析】解:∵,
∴,
∵是的平分线,
∴,故B正确.
故选:B.
5.
【解析】解:∵直角三角板的直角顶点在直线上,
∴
∵
∴
故选:
6.
【解析】解:A、,不能判断,选项错误;
B、,可以判断,不能判断,选项错误;
C、,可以判断,不能判断,选项错误;
D、,可以判断,选项正确,
故选D.
7.
【解析】解:过点C作,过点D作,
∵,
∴,
∴,
∵,,
由①②得:.
即
故选:B.
8.
【解析】解:如图①,
∵ADBC
∴∠A=∠CMB
∵AEBF
∴∠B=∠CMB
∴∠B=∠A=36°;
如图②,
∵ADBC
∴∠A=∠ANB
∵AEBF
∴∠B+∠ANB=180°
∴∠B+∠A=180°,
∴∠B=144°,
故选:C.
9.
【解析】解:由平移的性质知,
∴,即,
∴ cm,
即平移的距离是4cm.
故答案为:4cm.
10.
【解析】解:如图:
∵,
∴∠A+∠2=180°,
∵∠A=50°,
∴∠1=∠2=180°﹣∠A=180°﹣50°=130°.
故答案为:130°.
11.
【解析】解:∵,
∴,
由折叠性质得,,
∴.
故答案为:.
12.
【解析】解:由∠A+∠B=180°,可得:ADBC,理由是同旁内角互补,两直线平行;
故答案为:同旁内角互补,两直线平行.
13.
【解析】∵,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴.
14.
【解析】解:如图:
∵,
∴,
∵,
∴当时,,
∴直线b绕点A逆时针旋转.
故答案为:42.
15.
【解析】解:当时,
∵,
∴∠A+∠ACB=,
∵,
∴,
∵∠ECB=,
∴;
当时,
∵,
∴.
故答案为:或.
16.
【解析】解:灯P照射一次,需要秒,灯Q照射一次,需要秒,设开启秒后,两灯的光束互相垂直;
①当时,两灯光垂直于点,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
②当时,灯光返回,第一次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
③当时,灯光返回,第二次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
综上:开启秒或秒或秒时,两灯的光束互相垂直.
17.
【解析】(1)解:根据平移的性质,作图如下,
所在位置即为所求图形的位置.
(2)解:如图所示,连接、,
∵网格中每个小正方形的边长均为1,
∴的长,过点作延长线于,
则的高,
∴三角形的面积为,
故答案为:.
18.
【解析】证明:∵∠C=∠DAC,
∴ADBC,
∴∠DAE=∠B,
又∠C=∠B,
∴∠DAE=∠DAC,
∴AD平分∠CAE.
19.
【解析】证明:(已知),
(垂直的定义),
,
,
即,,
又(已知),
(等角的余角相等),
(内错角相等,两直线平行).
20.
【解析】解:∵∠1=∠2,
∴AB∥CD,
∴∠ADC+∠A=180°,
∴∠ADC=180°-75°=105°.
21.
【解析】解:∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
22.
【解析】解:(对顶角相等),
,
.
(两直线平行,同旁内角互补).
.
23.
【解析】证明:∵,
∴,
∴,
∵,
∴,
∴.
24.
【解析】解:,理由如下:
过点E作.
∴.
∵,
∴
∵,
∴(垂直定义).
∵,
∴.
∵,
∴.
∴.
∵,
∴.
25.
【解析】(1)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
①当转动50秒时,,
∴,
∴,
故答案为:15°;
②比值为:,理由如下,
如图2,过点作,
∵,
∴,
设两灯转动时间为秒,则,,
∴,,
∴,
即,
又∵,
即,
而,
∴
.
∴.
即比值为:;
(2)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
设A灯转动秒,两灯的光束互相平行,
A灯先转动30秒,则AQ转到AP还需要180-30=150(秒)
即,
①当B射线第一次垂直MN时,用时90÷3=30(秒),
此时A射线共计运动30+30=60秒,即,
即在灯射线到达之前,如图3所示,
∵,,
∴,,
∴,
∴,
即有:,
解得:(秒);
②如图4,在灯射线到达之后,回到前,
根据①中,同理有:
∵
即有:,
解得:.
③如图5,在灯射线回到后,第二次到前,
由题意得:
,解得:(舍去).
综上所述,灯转动15秒或82.5秒时,两灯的光束互相平行.
第1章 平 行 线
时间:100分 总分120分
一、选择题(每题3分,共24分)
1.以下运动属于平移运动的是 ( )
A.彩旗飘飘 B.荡秋千 C.电梯升降 D.折纸
2.图中与是同位角的有 ( )
A.1个 B.2个 C.3个 D.4个
3.下列图形中,根据AB∥CD,能得到的是 ( )
A. B.
C. D.
4.如图,是的平分线,,若,则的度数为( )
A.17.5° B.35° C.55° D.70°
5.如图,已知a∥b,直角三角板的直角顶点在直线 a 上,若,则等于 ( )
A. B. C. D.
6.如图,下列说法中,正确的是 ( )
A.若,则 B.若,则
C.若,则 D.若,则
7.如图,,,探索图中角α,β,γ之间的关系式正确的是 ( )
A. B. C. D.
8.如果∠A=36°,且与∠B的两条边分别平行,则∠B为 ( )
A.36° B.144° C.36°或144° D.36°或54°
二、填空题(每题3分,共24分)
9.将沿射线方向平移到的位置(点在线段上),如图,若,,则平移的距离是________.
10.如图,,∠A=50°,则∠1=_____.
11.如图,点是长方形纸片的边上一点,沿折叠纸片交于点,且,则的度数是______.
12.如图,由∠A+∠B=180°,可得:ADBC.理由是________.
13.如图,若,EF与AB,CD分别相交于点E,F,,平分线与EP相交于点P,,则__________°.
14.如图,,,若使,则可将直线b绕点A逆时针旋转___________度.
15.将两块透明的三角尺的直角顶点按如图所示的方式叠放在一起(其中,,),将绕点转动,满足点在直线的上方,且小于,当这两块三角尺有一组边互相平行时,的度数为______.
16.沈阳市政府拟定在中央公园建设大型灯光秀,在某平行湖道两岸所在直线、安装探照灯,若灯P发出的光束自逆时针旋转至便立即回转,灯Q发出的光束自逆时针旋转至便立即回转,每天晚间两灯同时开启不停交叉照射巡视.设灯P光束转动的速度是10度/秒,灯Q光束转动的速度是4度/秒,在两灯同时开启后的35秒内,开启______秒时,两灯的光束互相垂直.
三、解答题(每题8分,共72分)
17.如图,网格中每个小正方形的边长均为1,点、、均在小正方形的顶点,把三角形平移得到三角形,使点的对应点为.
(1)请在图中画出三角形.
(2)连接、,直接写出三角形的面积为___________.
18.如图所示,已知∠B=∠C=∠DAC,求证:AD平分∠CAE.
19.已知:如图,,,.求证:.
20.如图,∠1=∠2,∠A=75°,求∠ADC的度数.
21.如图,分别与交于点G、H,分别与交于点B、C,分别与交于点D、E,.若,,求的度数.
22.如图,直线,被直线所截,已知,,求和的度数.
23.如图,E在四边形的边的延长线上,连接BE交AD于F,已知,,求证:AB∥CD.
24.如图,E是线段上一点,与平行吗?为什么?
25.长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即,连结,且.灯射线自顺时针旋转至便立即回转,灯射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是1度/秒,灯转动的速度是3度/秒.
(1)若两灯同时转动,在灯射线第一次转到之前,两灯射出的光线交于点.
①如图1,当两灯光线同时转动50秒时,求的度数.
②如图2,过作交于点,则在转动过程中,求与的比值,并说明理由.
(2)若灯射线先转动30秒,灯射线才开始转动,在灯射线第一次转到之前,灯转动几秒,两灯的光线互相平行?
参考答案:
1.
【解析】解:A、不属于平移,故此选项错误;
B、属于旋转,故此选项错误;
C、属于平移,故此选项正确;
D、属于翻折变换,故此选项错误;
故选:C.
2.
【解析】解:第1个图和第4个图中的与是同位角,有2个,
故选:B.
3.
【解析】解:A.∵,
∴,
故选项不符合题意;
B.∵,
∴,得不到,
故选项不符合题意;
C.如图,
∵,
∴,
∵,
∴,
故选项正确,符合题意;
D.由得不到,故选项不符合题意.
故选:C.
4.
【解析】解:∵,
∴,
∵是的平分线,
∴,故B正确.
故选:B.
5.
【解析】解:∵直角三角板的直角顶点在直线上,
∴
∵
∴
故选:
6.
【解析】解:A、,不能判断,选项错误;
B、,可以判断,不能判断,选项错误;
C、,可以判断,不能判断,选项错误;
D、,可以判断,选项正确,
故选D.
7.
【解析】解:过点C作,过点D作,
∵,
∴,
∴,
∵,,
由①②得:.
即
故选:B.
8.
【解析】解:如图①,
∵ADBC
∴∠A=∠CMB
∵AEBF
∴∠B=∠CMB
∴∠B=∠A=36°;
如图②,
∵ADBC
∴∠A=∠ANB
∵AEBF
∴∠B+∠ANB=180°
∴∠B+∠A=180°,
∴∠B=144°,
故选:C.
9.
【解析】解:由平移的性质知,
∴,即,
∴ cm,
即平移的距离是4cm.
故答案为:4cm.
10.
【解析】解:如图:
∵,
∴∠A+∠2=180°,
∵∠A=50°,
∴∠1=∠2=180°﹣∠A=180°﹣50°=130°.
故答案为:130°.
11.
【解析】解:∵,
∴,
由折叠性质得,,
∴.
故答案为:.
12.
【解析】解:由∠A+∠B=180°,可得:ADBC,理由是同旁内角互补,两直线平行;
故答案为:同旁内角互补,两直线平行.
13.
【解析】∵,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴.
14.
【解析】解:如图:
∵,
∴,
∵,
∴当时,,
∴直线b绕点A逆时针旋转.
故答案为:42.
15.
【解析】解:当时,
∵,
∴∠A+∠ACB=,
∵,
∴,
∵∠ECB=,
∴;
当时,
∵,
∴.
故答案为:或.
16.
【解析】解:灯P照射一次,需要秒,灯Q照射一次,需要秒,设开启秒后,两灯的光束互相垂直;
①当时,两灯光垂直于点,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
②当时,灯光返回,第一次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
③当时,灯光返回,第二次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
综上:开启秒或秒或秒时,两灯的光束互相垂直.
17.
【解析】(1)解:根据平移的性质,作图如下,
所在位置即为所求图形的位置.
(2)解:如图所示,连接、,
∵网格中每个小正方形的边长均为1,
∴的长,过点作延长线于,
则的高,
∴三角形的面积为,
故答案为:.
18.
【解析】证明:∵∠C=∠DAC,
∴ADBC,
∴∠DAE=∠B,
又∠C=∠B,
∴∠DAE=∠DAC,
∴AD平分∠CAE.
19.
【解析】证明:(已知),
(垂直的定义),
,
,
即,,
又(已知),
(等角的余角相等),
(内错角相等,两直线平行).
20.
【解析】解:∵∠1=∠2,
∴AB∥CD,
∴∠ADC+∠A=180°,
∴∠ADC=180°-75°=105°.
21.
【解析】解:∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
22.
【解析】解:(对顶角相等),
,
.
(两直线平行,同旁内角互补).
.
23.
【解析】证明:∵,
∴,
∴,
∵,
∴,
∴.
24.
【解析】解:,理由如下:
过点E作.
∴.
∵,
∴
∵,
∴(垂直定义).
∵,
∴.
∵,
∴.
∴.
∵,
∴.
25.
【解析】(1)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
①当转动50秒时,,
∴,
∴,
故答案为:15°;
②比值为:,理由如下,
如图2,过点作,
∵,
∴,
设两灯转动时间为秒,则,,
∴,,
∴,
即,
又∵,
即,
而,
∴
.
∴.
即比值为:;
(2)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
设A灯转动秒,两灯的光束互相平行,
A灯先转动30秒,则AQ转到AP还需要180-30=150(秒)
即,
①当B射线第一次垂直MN时,用时90÷3=30(秒),
此时A射线共计运动30+30=60秒,即,
即在灯射线到达之前,如图3所示,
∵,,
∴,,
∴,
∴,
即有:,
解得:(秒);
②如图4,在灯射线到达之后,回到前,
根据①中,同理有:
∵
即有:,
解得:.
③如图5,在灯射线回到后,第二次到前,
由题意得:
,解得:(舍去).
综上所述,灯转动15秒或82.5秒时,两灯的光束互相平行.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
