3.3多项式的乘法(1).

课件13张PPT。1、单项式与单项式相乘的法则？ ①2x2·(-4xy)=
②(-2x2)·(-3xy2)=
③(-9a2 b3)·(8ab2) =
④12×( － + )=-72a3 b59 单项式与单项式相乘，只要将它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式.-8x3y6x3y2单项式与多项式相乘的法则：2: 单项式与多项式相乘,就是用单项式去乘
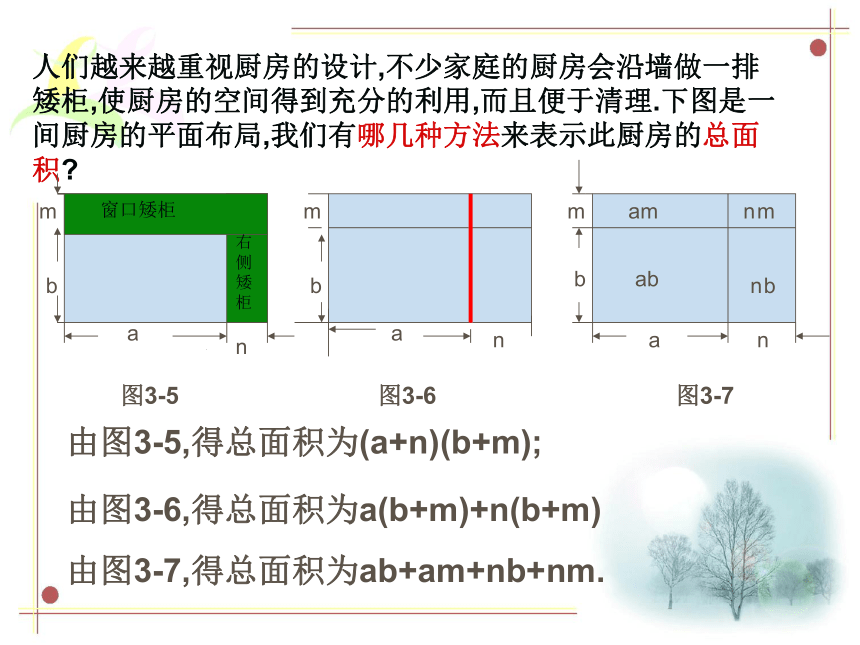
再把所得的积相加多项式的每一项3.3多项式的乘法（1）人们越来越重视厨房的设计,不少家庭的厨房会沿墙做一排矮柜,使厨房的空间得到充分的利用,而且便于清理.下图是一间厨房的平面布局,我们有哪几种方法来表示此厨房的总面积?bambamabamb窗口矮柜右侧矮柜an图3-5图3-6图3-7由图3-5,得总面积为(a+n)(b+m);由图3-6,得总面积为a(b+m)+n(b+m)nmnbn由图3-7,得总面积为ab+am+nb+nm.nm由此,我们可以得到什么结论呢?(a+n)(b+m)多项式与多项式相乘的法则:即(a+n)(b+m)=多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.=ab+am+nb+nm=a(b+m)+n(b+m)ab+am+nb+nm(1)(x+y)(a+2b); (2) (3x-1)(x+3)注意:多项式与多项式相乘的结果中,要把同类项合并.例1 计算:
解:原式解:原式例2、先化简，再求值：其中原式=6a2－9a+2a－3－6a2+24a=17a－3当a= 时原式=17× －3=－1多项式乘法法则的应用一：先化简,再求值:
、练一练：2、化简求值：
5x（1-2x）+（x+1）（10x-2）
其中x= 你注意到了吗？ 多项式乘以多项式，展开后项数很有规律，在合并同类项之前，展开式的项数恰好等于两个多项式的项数的积。观察下列各式计算结果与相乘的两个多项式之间的关系，你能发现什么规律？并按规律做题：二次项是这个相同字母的平方(x2)；一次项系数是两个常数的和，常数项是两个常数的积．(x+a)(x+b)＝x2+(a+b)x+ab试一试:
1.若(x+a)(x+b)中不含x的一次项,则a与b的关系是 ( )
(A)a=b=0 (B)a-b=0 (C)a=b≠0
(D)a+b=0B努力啊，孩子们！