2.4 二元一次方程组的应用 教学课件(2课时)
文档属性
| 名称 | 2.4 二元一次方程组的应用 教学课件(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 583.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-10 00:00:00 | ||
图片预览





文档简介
课件27张PPT。2.4 二元一次方程组的应用
(第一课时)浙教版七年级下册第2章 二元一次方程组 游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?思考下面几个问题:
1.问题中所求的未知数有几个?
2.有哪些等量关系?
3.怎样设未知数?可以列出几个方程?
4.本题能列一元一次方程吗?用列二元一次方程组的方法求解,有什么优点? 男孩人数-1=女孩人数;
男孩人数=2(女孩人数-1).合作学习合作学习:游泳池中的数学问题 游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?解:设男孩x人,女孩y人,则由题意,得x-1=y,
x=2(y-1).x-y=1,
x-2y=-2.整理得x=4,
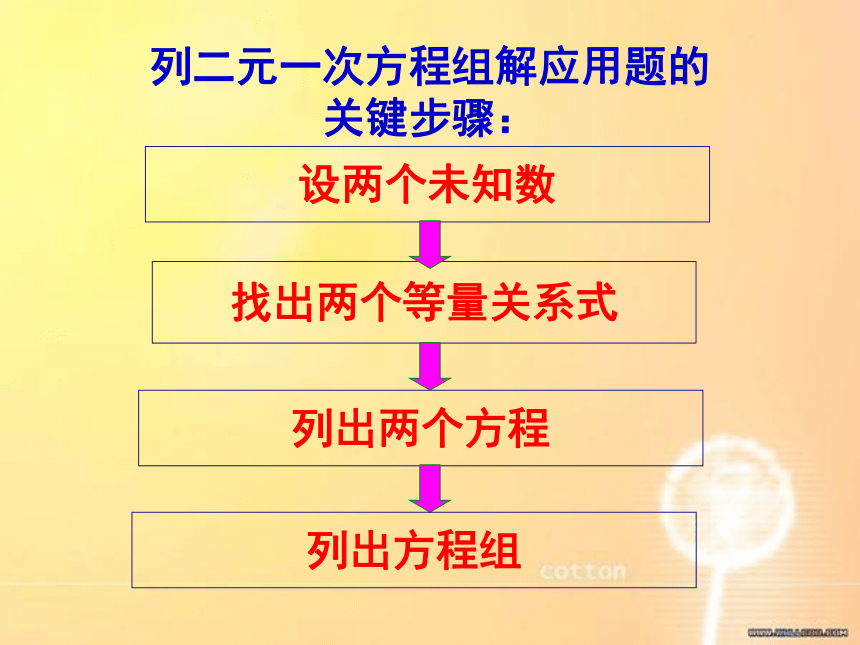
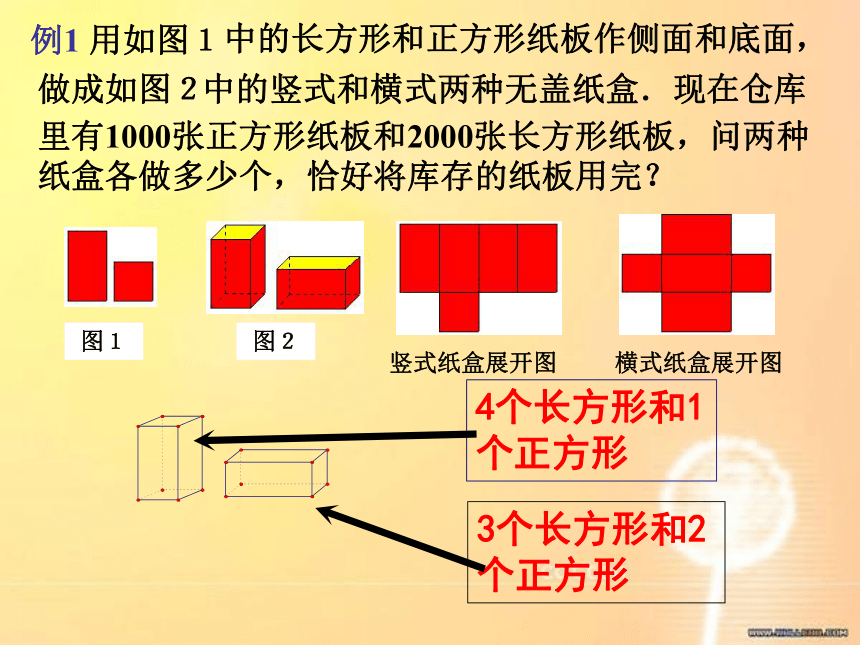
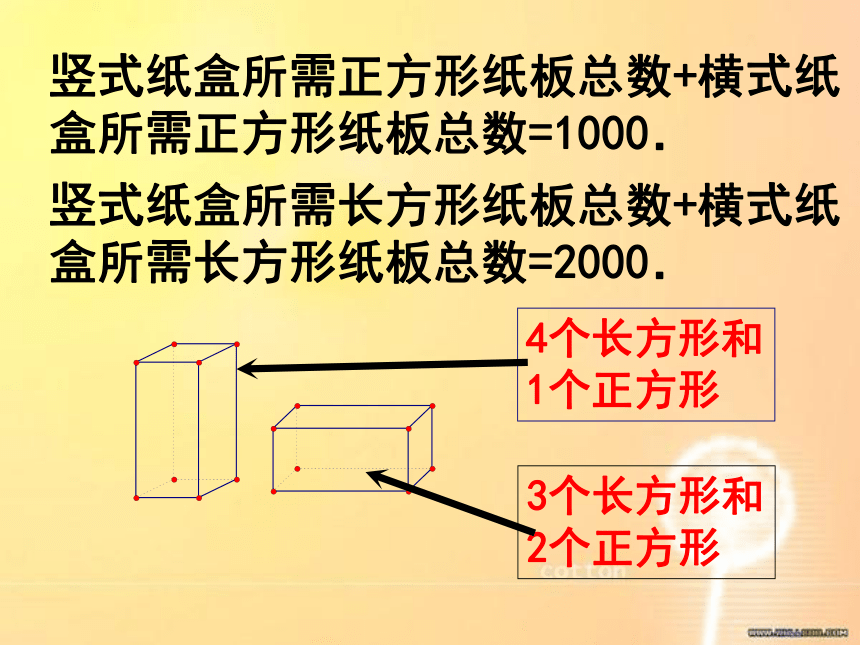
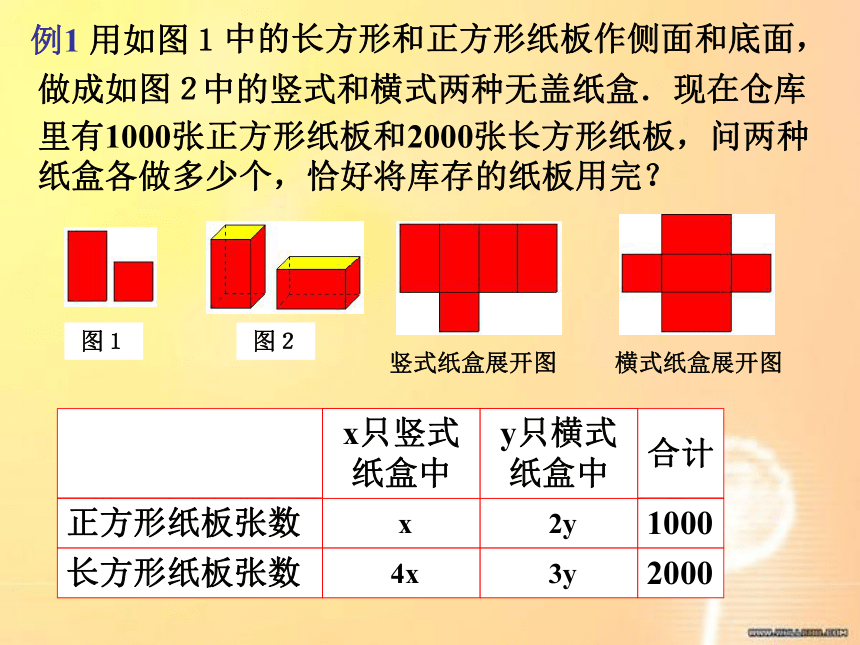
y=3.解得答:男孩有4人,女孩有3人.2.必须设两个未知数,找出两个等量关系,列两个不同的方程.归纳:1.列二元一次方程组解决问题,能使问题变得简单,比较容易找出等量关系.找出两个等量关系式列二元一次方程组解应用题的 关键步骤:列出两个方程设两个未知数列出方程组 在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表、画线段图分析数量关系是常用的方法.2、两个数字,甲数比乙数的4倍少5,乙数比甲数的3倍多4,求这两个数.基础训练1、某工地派96人去挖土和运土,如果平均每人挖土5m3或运土3m3,那么怎样分配挖土和运土的人数,才能使挖出的土刚好能被运完?快速列出方程组里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?竖式纸盒展开图横式纸盒展开图例1 用如图1中的长方形和正方形纸板作侧面和底面,做成如图2中的竖式和横式两种无盖纸盒.现在仓库图1图2竖式纸盒所需正方形纸板总数+横式纸盒所需正方形纸板总数=1000.竖式纸盒所需长方形纸板总数+横式纸盒所需长方形纸板总数=2000.做一个竖式盒子要用几张长方形纸板和几张正方形纸板?里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?竖式纸盒展开图横式纸盒展开图例1 用如图1中的长方形和正方形纸板作侧面和底面,做成如图2中的竖式和横式两种无盖纸盒.现在仓库分析:x2y4x3y图1图2 列二元一次方程组解应用题的步骤:
1.理解问题(审题,搞清已知和未知,分析数 量关系)
2.制订计划(考虑如何根据等量关系设元,列出方程组)
3.执行计划(列出方程组并求解,得到答案)
4.回顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)
上题中如果改为库存正方形纸板500张,长方形纸板1001张,那么,能否做成若干只竖式纸盒和若干只横式纸盒后,恰好把库存纸板用完?练习x2y4x3y竖式纸盒展开图横式纸盒展开图图一图二解:设做竖式纸盒x个,做横式纸盒y个,根据题意,得y不是自然数,不合题意,所以当库存正方形纸板500张,长方形纸板1001张时不可能做成若干个纸盒后恰好将库存的纸板用完.甲、乙两人从相距36千米的两地匀速相向而行.如果甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇;如果乙比甲先走2小时,那么他们在甲出发后经3小时相遇.求甲、乙两人每时各走多少千米?36千米甲先行2时走的路程乙出发后甲、乙2.5时共走路程相遇相遇36千米甲出发后甲、乙3时共走路程乙先行2时走的路程 今有牛五、马二,直金十两.
牛二、马五,直金八两.
牛、马各直几何?有一道这样的题:
“100个和尚吃100个馒头.
大和尚一人吃3个,
小和尚3人吃一个.
求大、小和尚各多少个?”2.4 二元一次方程组的应用 (第二课时)浙教版七年级下册第2章 二元一次方程组应用二元一次方程组解决实际问题的基本步骤:(1)理解问题 (审题,搞清已知和未知,分析数量关系)(2)制定计划 (考虑如何根据等量关系设元,列出方程组)(3)执行计划 (列出方程组并求解,得到答案)(4)回顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)回 顾例2 一根金属棒在0℃时的长度是q(m),温度每升高1℃,它就伸长p(m).当温度为t(℃)时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100℃时,L=2.002m;当t=500℃时,L=2.01m.(1)求p,q的值;(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?(1)问题中含有几个未知数?需列几个方程?要找出几个相等的关系?(2)从已知条件“当t=100℃时,L=2.002m;当t=500℃时,L=2.01m”你能得到怎样的相等关系?这两个相等关系从方程角度看是关于什么未知数的方程?问题中含有2个未知数,需列2个方程,要找出2个相等的关系. 分析:可得两个相等的关系式:100p+q=2.002,500p+q=2.01. 练一练将大拇指与小拇指尽量张开时,两指间的距离称为指距.研究表明,一般情况下,人的身高h和指距d之间有关系式h=ad+k .下表是测得一些人的指距与身高的一组数据:
指距d(cm) 20 21 22 23 …
身高h(cm) 160 169 178 187 …
(1)求a,k;
(2)某人身高为196 cm,他的指距估计是多少? 例3 通过对一份中学生营养快餐的检测,得到以下信息: ①快餐总质量为300g; ②快餐的成分:蛋白质、碳水化合物、脂肪、矿物质; ③蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍; 蛋白质和碳水化合物含量占85%. 根据上述数据回答下面的问题: (1)分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质 的质量和所占百分比; (2)根据计算结果制作扇形统计图表示营养快餐成分的信息.分析:本题有多个未知量,因此请同学们注意以下几个问题:1.本题有哪些已知量?
本题目中的已知量:快餐总质量、蛋白质和脂肪含量的百分
比、蛋白质和碳水化合物含量的百分比.2.本题有哪些未知量?要求什么?3.蛋白质、碳水化合物、脂肪、矿物质这四个未知量中,哪两个与已知量和其他未知量都有已知的数量关系?什么样的已知关系?本题有四个未知量分别为:蛋白质、碳水化合物、脂肪、矿物质.要求的是四种成分的质量和百分比. 矿物质量含量=脂肪含量 2 蛋白质含量+碳水化合物含量=快餐总质量 85% 蛋白质含量+脂肪含量=快餐总质量 50% 矿物质量含量+碳水化合物含量=快餐总质量 50%如何根据以上的等量关系设未知量呢? 根据等量关系不妨设:一份营养快餐中含蛋白质为x(g),脂肪为y(g),则含矿物质为 (g),碳水化合物为 (g),
由等量关系可列出方程组.
2y (300×85%-x) 解:设一份营养快餐中含蛋白质为x(g),脂肪为y(g),则含矿物质为2y(g),碳水化合物为(300×85%-x)(g),由题意,得①+②,得 ,解得 ∴根据以上计算,我们可以制出统计表,如下:13545155301012040300100 1、 用二元一次方程组解实际问题的基本步骤审、设、列、解、检、答2、 如何设元回顾与反思分析抽象方程(组)求解检验问题解决实际问题 1.小强和小明做算术题, 小强将第一个加数的后面多写一个零, 所得和是2342; 小明将第一个加数的后面少写一个零, 所得和是65.求原来的两个加数分别是多少?
思考与练习 2.A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时匀速相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求甲、乙二人的速度?
(第一课时)浙教版七年级下册第2章 二元一次方程组 游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?思考下面几个问题:
1.问题中所求的未知数有几个?
2.有哪些等量关系?
3.怎样设未知数?可以列出几个方程?
4.本题能列一元一次方程吗?用列二元一次方程组的方法求解,有什么优点? 男孩人数-1=女孩人数;
男孩人数=2(女孩人数-1).合作学习合作学习:游泳池中的数学问题 游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?解:设男孩x人,女孩y人,则由题意,得x-1=y,
x=2(y-1).x-y=1,
x-2y=-2.整理得x=4,
y=3.解得答:男孩有4人,女孩有3人.2.必须设两个未知数,找出两个等量关系,列两个不同的方程.归纳:1.列二元一次方程组解决问题,能使问题变得简单,比较容易找出等量关系.找出两个等量关系式列二元一次方程组解应用题的 关键步骤:列出两个方程设两个未知数列出方程组 在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表、画线段图分析数量关系是常用的方法.2、两个数字,甲数比乙数的4倍少5,乙数比甲数的3倍多4,求这两个数.基础训练1、某工地派96人去挖土和运土,如果平均每人挖土5m3或运土3m3,那么怎样分配挖土和运土的人数,才能使挖出的土刚好能被运完?快速列出方程组里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?竖式纸盒展开图横式纸盒展开图例1 用如图1中的长方形和正方形纸板作侧面和底面,做成如图2中的竖式和横式两种无盖纸盒.现在仓库图1图2竖式纸盒所需正方形纸板总数+横式纸盒所需正方形纸板总数=1000.竖式纸盒所需长方形纸板总数+横式纸盒所需长方形纸板总数=2000.做一个竖式盒子要用几张长方形纸板和几张正方形纸板?里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?竖式纸盒展开图横式纸盒展开图例1 用如图1中的长方形和正方形纸板作侧面和底面,做成如图2中的竖式和横式两种无盖纸盒.现在仓库分析:x2y4x3y图1图2 列二元一次方程组解应用题的步骤:
1.理解问题(审题,搞清已知和未知,分析数 量关系)
2.制订计划(考虑如何根据等量关系设元,列出方程组)
3.执行计划(列出方程组并求解,得到答案)
4.回顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)
上题中如果改为库存正方形纸板500张,长方形纸板1001张,那么,能否做成若干只竖式纸盒和若干只横式纸盒后,恰好把库存纸板用完?练习x2y4x3y竖式纸盒展开图横式纸盒展开图图一图二解:设做竖式纸盒x个,做横式纸盒y个,根据题意,得y不是自然数,不合题意,所以当库存正方形纸板500张,长方形纸板1001张时不可能做成若干个纸盒后恰好将库存的纸板用完.甲、乙两人从相距36千米的两地匀速相向而行.如果甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇;如果乙比甲先走2小时,那么他们在甲出发后经3小时相遇.求甲、乙两人每时各走多少千米?36千米甲先行2时走的路程乙出发后甲、乙2.5时共走路程相遇相遇36千米甲出发后甲、乙3时共走路程乙先行2时走的路程 今有牛五、马二,直金十两.
牛二、马五,直金八两.
牛、马各直几何?有一道这样的题:
“100个和尚吃100个馒头.
大和尚一人吃3个,
小和尚3人吃一个.
求大、小和尚各多少个?”2.4 二元一次方程组的应用 (第二课时)浙教版七年级下册第2章 二元一次方程组应用二元一次方程组解决实际问题的基本步骤:(1)理解问题 (审题,搞清已知和未知,分析数量关系)(2)制定计划 (考虑如何根据等量关系设元,列出方程组)(3)执行计划 (列出方程组并求解,得到答案)(4)回顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)回 顾例2 一根金属棒在0℃时的长度是q(m),温度每升高1℃,它就伸长p(m).当温度为t(℃)时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100℃时,L=2.002m;当t=500℃时,L=2.01m.(1)求p,q的值;(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?(1)问题中含有几个未知数?需列几个方程?要找出几个相等的关系?(2)从已知条件“当t=100℃时,L=2.002m;当t=500℃时,L=2.01m”你能得到怎样的相等关系?这两个相等关系从方程角度看是关于什么未知数的方程?问题中含有2个未知数,需列2个方程,要找出2个相等的关系. 分析:可得两个相等的关系式:100p+q=2.002,500p+q=2.01. 练一练将大拇指与小拇指尽量张开时,两指间的距离称为指距.研究表明,一般情况下,人的身高h和指距d之间有关系式h=ad+k .下表是测得一些人的指距与身高的一组数据:
指距d(cm) 20 21 22 23 …
身高h(cm) 160 169 178 187 …
(1)求a,k;
(2)某人身高为196 cm,他的指距估计是多少? 例3 通过对一份中学生营养快餐的检测,得到以下信息: ①快餐总质量为300g; ②快餐的成分:蛋白质、碳水化合物、脂肪、矿物质; ③蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍; 蛋白质和碳水化合物含量占85%. 根据上述数据回答下面的问题: (1)分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质 的质量和所占百分比; (2)根据计算结果制作扇形统计图表示营养快餐成分的信息.分析:本题有多个未知量,因此请同学们注意以下几个问题:1.本题有哪些已知量?
本题目中的已知量:快餐总质量、蛋白质和脂肪含量的百分
比、蛋白质和碳水化合物含量的百分比.2.本题有哪些未知量?要求什么?3.蛋白质、碳水化合物、脂肪、矿物质这四个未知量中,哪两个与已知量和其他未知量都有已知的数量关系?什么样的已知关系?本题有四个未知量分别为:蛋白质、碳水化合物、脂肪、矿物质.要求的是四种成分的质量和百分比. 矿物质量含量=脂肪含量 2 蛋白质含量+碳水化合物含量=快餐总质量 85% 蛋白质含量+脂肪含量=快餐总质量 50% 矿物质量含量+碳水化合物含量=快餐总质量 50%如何根据以上的等量关系设未知量呢? 根据等量关系不妨设:一份营养快餐中含蛋白质为x(g),脂肪为y(g),则含矿物质为 (g),碳水化合物为 (g),
由等量关系可列出方程组.
2y (300×85%-x) 解:设一份营养快餐中含蛋白质为x(g),脂肪为y(g),则含矿物质为2y(g),碳水化合物为(300×85%-x)(g),由题意,得①+②,得 ,解得 ∴根据以上计算,我们可以制出统计表,如下:13545155301012040300100 1、 用二元一次方程组解实际问题的基本步骤审、设、列、解、检、答2、 如何设元回顾与反思分析抽象方程(组)求解检验问题解决实际问题 1.小强和小明做算术题, 小强将第一个加数的后面多写一个零, 所得和是2342; 小明将第一个加数的后面少写一个零, 所得和是65.求原来的两个加数分别是多少?
思考与练习 2.A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时匀速相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求甲、乙二人的速度?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
