浙教版2023年七年级下册1.4 平行线的性质 同步练习卷(含详解)
文档属性
| 名称 | 浙教版2023年七年级下册1.4 平行线的性质 同步练习卷(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 341.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 13:27:51 | ||
图片预览




文档简介
浙教版2023年七年级下册1.4 平行线的性质 同步练习卷
一.选择题
1.已知:如图,直线a,b被直线c所截,且a∥b,若∠2=110°,则∠1的度数是( )
A.130° B.110° C.80° D.70°
2.如图,AB∥DE,BC∥EF,则∠E与∠B的关系一定成立的是( )
A.互余 B.∠E=2∠B C.相等 D.互补
3.如图,已知a∥c,添加下列条件后,能推出b∥c的是( )
A.∠5+∠2=180° B.∠3=∠6 C.∠4+∠6=180° D.∠1=∠2
4.将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )
A.30° B.40° C.50° D.60°
5.如图,AB∥CD,∠ABM=30°,∠CDM=45°,则∠BMD的度数为( )
A.105° B.90° C.75° D.70°
6.如图,一个宽度相等的纸条按如图所示的方法折叠一下,若∠2=132°,则∠1=( )
A.61° B.66° C.52° D.132°
7.如图,AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数是( )
A.10° B.20° C.50° D.110°
二.填空题
8.如图,已知AB∥CD,∠2=70°,则∠1= °.
9.如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠EDA=128°,则∠CBD的大小为 度.
10.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是70°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是161°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于 .
11.已知AB∥CD,∠BAD=40°,点M在直线AD上,N为线段CD上一点,若∠MNC=α,则∠AMN= .(用含α的式子表示)
12.如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠B= .
13.将一副三角板按如图放置,则下列结论:①如果∠2=30°,则AC∥DE;②∠2+∠CAD=180°;③如果BC∥AD,则有∠2=60°;④如果∠CAD=150°,必有∠4=∠C;其中正确的结论有 .
14.已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,请直接写出α、β、γ的数量关系 .
三.解答题
15.完成下列推理说明:
如图,∠BAM=75°,∠BGE=75°,∠CHG=105°,可推出AM∥EF,AB∥CD,完成下列空白:
∵∠BAM=75°,∠BGE=75°,
∴∠BAM=∠BGE( ).
∴ ∥ ( ).
∴∠AGH=∠BAM=75°( ).
∵∠CHG=105°,
∴∠AGH+∠CHG=75°+105°=180°( ).
∴ ∥ ( ).
16.如图,点D,点E分别在∠BAC的边AB,AC上,点F在∠BAC内,EF∥AB,且∠F=∠A,求证:DF∥AC.
17.将下面的推理过程及依据补充完整.
已知:如图,CD平分∠ACB,AC∥DE,CD∥EF.
求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠ACD= .
∵AC∥DE(已知),
∴∠ACD= ( ),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴ =∠CDE( ),
∠DCE= ( ),
∴ = (等量代换),
∴EF平分∠DEB.
18.如图,已知BD⊥AC,EF⊥AC,点D,F是垂足,∠1+∠C=90°.
(1)求证:DG∥BC;
(2)若BD平分∠ABC,∠C=50°,求∠BGD的度数.
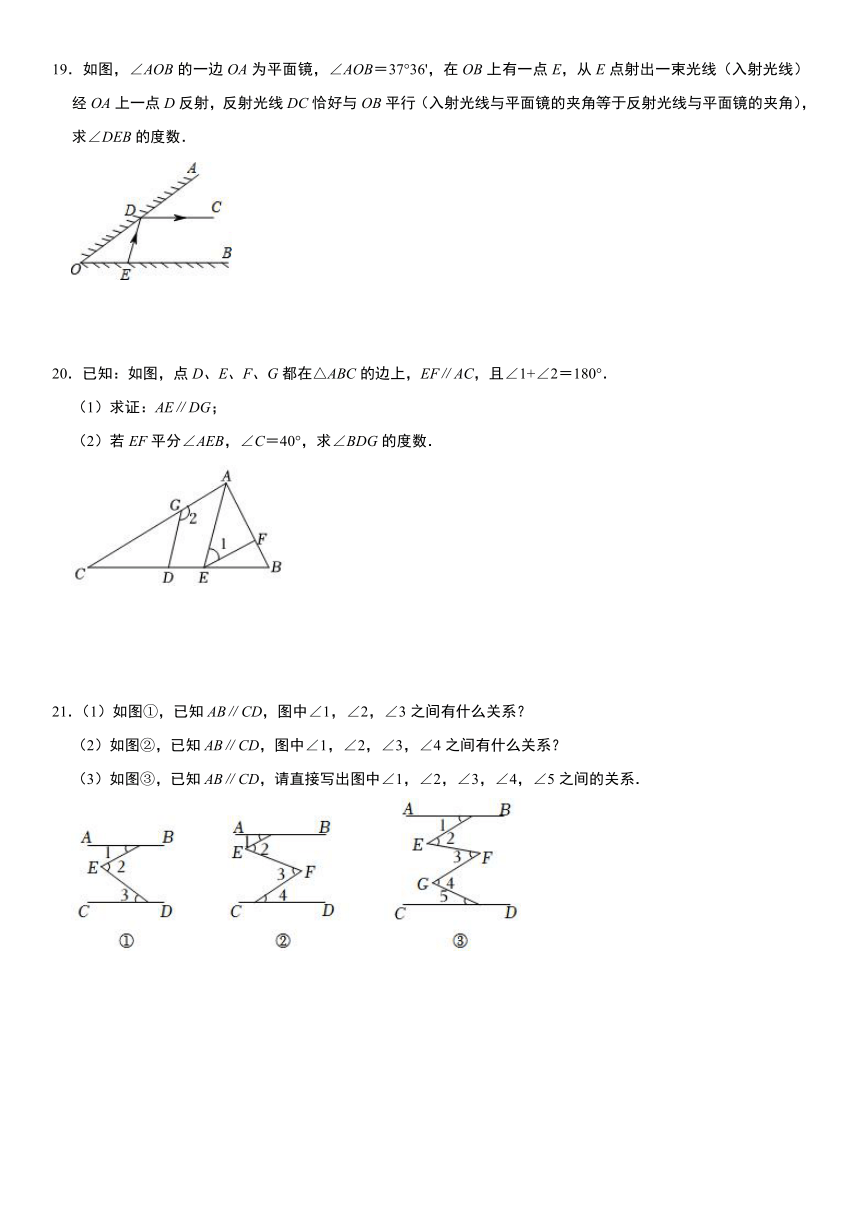
19.如图,∠AOB的一边OA为平面镜,∠AOB=37°36',在OB上有一点E,从E点射出一束光线(入射光线)经OA上一点D反射,反射光线DC恰好与OB平行(入射光线与平面镜的夹角等于反射光线与平面镜的夹角),求∠DEB的度数.
20.已知:如图,点D、E、F、G都在△ABC的边上,EF∥AC,且∠1+∠2=180°.
(1)求证:AE∥DG;
(2)若EF平分∠AEB,∠C=40°,求∠BDG的度数.
21.(1)如图①,已知AB∥CD,图中∠1,∠2,∠3之间有什么关系?
(2)如图②,已知AB∥CD,图中∠1,∠2,∠3,∠4之间有什么关系?
(3)如图③,已知AB∥CD,请直接写出图中∠1,∠2,∠3,∠4,∠5之间的关系.
参考答案
一.选择题
1.【解答】解:如图:
∵a∥b,∠2=110°,
∴∠3=∠2=110°,
∵∠1+∠3=180°,
∴∠1=70°.
故选:D.
2.【解答】解:如图,
∵AB∥DE,BC∥EF,
∴∠B=∠CGD,∠E=∠BGD,
∵∠CGD+∠BGD=180°,
∴∠B+∠E=180°,
即∠B与∠E互补.
故选:D.
3.【解答】解:∵∠5+∠2=180°,
∴a∥b,
∵a∥c,
∴b∥c,
故A符合题意;
由∠3=∠6,不能推出b∥c,
故B不符合题意;
由∠4+∠6=180°,不能推出b∥c,
故C不符合题意;
由∠1=∠2,不能推出b∥c,
故D不符合题意;
故选:A.
4.【解答】解:标出字母,如图:
∵∠3=∠2=40°,∠ACB=90°,
∴∠4=90°﹣∠3=50°,
∵DE∥FG,
∴∠1=∠4=50°.
故选:C.
5.【解答】解:过点M作ME∥AB,如图,
∵AB∥CD,
∴AB∥ME∥CD,
∴∠ABM=∠BME=30°,∠CDM=∠DME=45°,
∴∠BMD=∠BME+∠DME=75°.
故选:C.
6.【解答】解:如图,
∵AB∥CD,∠2=132°,
∴∠DMN=∠ANM=∠2=132°,
根据折叠的性质得,∠1=∠DME,∠DMN=∠1+∠MDE,
∴2∠1=132°,
解得:∠1=66°.
故选:B.
7.【解答】解:∵AB∥DE∥CF,∠ABC=70°,∠CDE=130°,
∴∠BCF=∠ABC=70°,∠DCF=180°﹣∠CDE=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°,
故选:B.
二.填空题
8.【解答】解:如图:
∵AB∥CD,
∴∠2=∠3=70°,
∴∠1=180°﹣∠3=110°,
故答案为:110°.
9.【解答】解:∵AD∥CB,
∴∠ADF=∠CBD,
∵∠EDA+∠ADF=180°,
∴∠ADF=180°﹣∠EDA=180°﹣128°=52°,
∴∠CBD=52°.
故答案为:52.
10.【解答】解:过B作BD∥AE,
∵AE∥CF,
∴BD∥CF,
∴∠A=∠ABD=70°,∠DBC+∠C=180°,
∵∠C=161°,
∴∠DBC=19°,
则∠ABC=∠ABD+∠DBC=89°.
故答案为:89°.
11.【解答】解:如图,当点M在线段AD上时,
过点M作ME∥AB,
∴∠AME=∠BAD=40°,
∵ME∥AB,AB∥CD,
∴ME∥CD,
∴∠EMN+∠MNC=180°,
∵∠MNC=α,
∴∠EMN=180°﹣α,
∴∠AMN=∠AME+∠EMN=40°+(180°﹣α)=220°﹣α;
如图,当点M在AD的延长线上时,
过点M作ME∥AB,
∴∠AME=∠BAD=40°,
∵ME∥AB,AB∥CD,
∴ME∥CD,
∴∠EMN+∠MNC=180°,
∵∠MNC=α,
∴∠EMN=180°﹣α,
∴∠AMN=∠AME﹣∠EMN=40°﹣(180°﹣α)=α﹣140°;
如图,当点M在DA的延长线上时,
过点M作ME∥AB,
∴∠AME=∠BAD=40°,
∵ME∥AB,AB∥CD,
∴ME∥CD,
∴∠EMN=∠MNC=α,
∴∠AMN=∠EMN﹣∠AME=α﹣40°;
故答案为:220°﹣α或α﹣140°或α﹣40°.
12.【解答】解:如图,过点B作l3∥l2,则∠2=∠1=43°,
∵BC与l2,
∴∠4=90°,
∵直线l1∥l2,
∴l1∥l3,
∴∠3=∠4=90°,
∴∠ABC=∠3+∠2=90°+43°=133°.
故答案为:133°.
13.【解答】解:∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,故①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,故②正确;
∵BC∥AD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90°﹣45°=45°,故③错误;
∵∠D=30°,∠CAD=150°,
∴∠CAD+∠D=180°,
∴AC∥DE,
∴∠4=∠C,故④正确.
故答案为:①②④.
14.【解答】解:γ+α=90°+β.理由如下:
作PF∥AB,如图,
可得∠ABE+∠EFP=∠BEF,
而∠PFC=∠FCD,
∴∠EFP=90°﹣α,∠PFC=β,
∴∠EFP+∠PFC=90°﹣α+β,
∴γ=90°﹣α+β,
即γ+α=90°+β.
故答案为:γ+α=90°+β.
三.解答题
15.【解答】解:∵∠BAM=75°,∠BGE=75°,
∴∠BAM=∠BGE(等量代换).
∴AM∥EF(同位角相等,两直线平行).
∴∠AGH=∠BAM=75°(两直线平行,内错角相等).
∵∠CHG=105°,
∴∠AGH+∠CHG=75°+105°=180°(角度计算).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:等量代换;AM;EF;同位角相等,两直线平行;两直线平行,内错角相等;角度计算;AB;CD;同旁内角互补,两直线平行.
16.【解答】证明:∵EF∥AB,
∴∠F=∠BDF,
又∵∠A=∠F,
∴∠A=∠BDF,
∴DF∥AC.
17.【解答】证明:∵CD平分∠ACB(已知),
∴∠ACD=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠ACD=∠CDE (两直线平行,内错角相等),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(角平分线的定义).
故答案为:∠DCE;∠CDE;两直线平行,内错角相等;∠DEF;两直线平行,内错角相等;∠FEB;两直线平行,同位角相等;∠DEF;∠FEB.
18.【解答】(1)证明:∵BD⊥AC,EF⊥AC,
∴∠3=∠4=90°,
∵∠1+∠C=90°,
∴∠CDG+∠C=∠1+∠3+∠C=180°,
∴DG∥BC;
(2)解:∵∠3=90°,∠C=50°,
∴∠DBC=180°﹣∠3﹣∠C=40°,
∵BD平分∠ABC,
∴∠CBG=2∠DBC=80°,
∵DG∥BC,
∴∠BGD+∠CBG=180°,
∴∠BGD=100°.
19.【解答】解:过点D作DF⊥AO交OB于点F.
∵入射角等于反射角,
∴∠1=∠3,
∵CD∥OB,
∴∠1=∠2,
∴∠2=∠3,
在Rt△DOF中,∠ODF=90°,∠AOB=37°36′,
∴∠2=90°﹣37°36′=52°24′;
在△DEF中,∠DEB=180°﹣2∠2=75°12′=75.2°.
20.【解答】(1)证明:∵EF∥AC,
∴∠CAE=∠1,
∵∠1+∠2=180°,
∴∠CAE+∠2=180°,
∴AE∥DG.
(2)解:∵EF∥AC,∠C=40°,
∴∠BEF=∠C=40°,
∵EF平分∠AEB,
∴∠BEF=∠1=40°,
∴∠AEB=80°,
由(1)知AE∥DG,
∴∠BDG=∠AEB=80°.
21.【解答】解:(1)如图①,过点E作EM∥AB,
∵AB∥CD,
∴AB∥CD∥EM,
∴∠1=∠NEM,∠3=∠MEF,
∴∠1+∠3=∠NEM=∠MEF,
即∠1+∠3=∠2;
(2)如图②,过点F作NF∥AB,
∵AB∥CD,
∴AB∥CD∥FN,
∴∠4=∠NFH,
由(1)知,∠1+∠EFN=∠2,
∴∠1+∠EFN+∠NFH=∠2+∠4,
即∠1+∠3=∠2+∠4;
(3)如图③,过点G作GM∥AB,
∵AB∥CD,
∴AB∥CD∥GM,
∴∠5=∠MGN,
由(2)得,∠1+∠3=∠2+∠FGM,
∴∠1+∠3+∠5=∠2+∠FGM+∠MGN,
即∠1+∠3+∠5=∠2+∠4.
一.选择题
1.已知:如图,直线a,b被直线c所截,且a∥b,若∠2=110°,则∠1的度数是( )
A.130° B.110° C.80° D.70°
2.如图,AB∥DE,BC∥EF,则∠E与∠B的关系一定成立的是( )
A.互余 B.∠E=2∠B C.相等 D.互补
3.如图,已知a∥c,添加下列条件后,能推出b∥c的是( )
A.∠5+∠2=180° B.∠3=∠6 C.∠4+∠6=180° D.∠1=∠2
4.将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )
A.30° B.40° C.50° D.60°
5.如图,AB∥CD,∠ABM=30°,∠CDM=45°,则∠BMD的度数为( )
A.105° B.90° C.75° D.70°
6.如图,一个宽度相等的纸条按如图所示的方法折叠一下,若∠2=132°,则∠1=( )
A.61° B.66° C.52° D.132°
7.如图,AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数是( )
A.10° B.20° C.50° D.110°
二.填空题
8.如图,已知AB∥CD,∠2=70°,则∠1= °.
9.如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠EDA=128°,则∠CBD的大小为 度.
10.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是70°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是161°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于 .
11.已知AB∥CD,∠BAD=40°,点M在直线AD上,N为线段CD上一点,若∠MNC=α,则∠AMN= .(用含α的式子表示)
12.如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠B= .
13.将一副三角板按如图放置,则下列结论:①如果∠2=30°,则AC∥DE;②∠2+∠CAD=180°;③如果BC∥AD,则有∠2=60°;④如果∠CAD=150°,必有∠4=∠C;其中正确的结论有 .
14.已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,请直接写出α、β、γ的数量关系 .
三.解答题
15.完成下列推理说明:
如图,∠BAM=75°,∠BGE=75°,∠CHG=105°,可推出AM∥EF,AB∥CD,完成下列空白:
∵∠BAM=75°,∠BGE=75°,
∴∠BAM=∠BGE( ).
∴ ∥ ( ).
∴∠AGH=∠BAM=75°( ).
∵∠CHG=105°,
∴∠AGH+∠CHG=75°+105°=180°( ).
∴ ∥ ( ).
16.如图,点D,点E分别在∠BAC的边AB,AC上,点F在∠BAC内,EF∥AB,且∠F=∠A,求证:DF∥AC.
17.将下面的推理过程及依据补充完整.
已知:如图,CD平分∠ACB,AC∥DE,CD∥EF.
求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠ACD= .
∵AC∥DE(已知),
∴∠ACD= ( ),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴ =∠CDE( ),
∠DCE= ( ),
∴ = (等量代换),
∴EF平分∠DEB.
18.如图,已知BD⊥AC,EF⊥AC,点D,F是垂足,∠1+∠C=90°.
(1)求证:DG∥BC;
(2)若BD平分∠ABC,∠C=50°,求∠BGD的度数.
19.如图,∠AOB的一边OA为平面镜,∠AOB=37°36',在OB上有一点E,从E点射出一束光线(入射光线)经OA上一点D反射,反射光线DC恰好与OB平行(入射光线与平面镜的夹角等于反射光线与平面镜的夹角),求∠DEB的度数.
20.已知:如图,点D、E、F、G都在△ABC的边上,EF∥AC,且∠1+∠2=180°.
(1)求证:AE∥DG;
(2)若EF平分∠AEB,∠C=40°,求∠BDG的度数.
21.(1)如图①,已知AB∥CD,图中∠1,∠2,∠3之间有什么关系?
(2)如图②,已知AB∥CD,图中∠1,∠2,∠3,∠4之间有什么关系?
(3)如图③,已知AB∥CD,请直接写出图中∠1,∠2,∠3,∠4,∠5之间的关系.
参考答案
一.选择题
1.【解答】解:如图:
∵a∥b,∠2=110°,
∴∠3=∠2=110°,
∵∠1+∠3=180°,
∴∠1=70°.
故选:D.
2.【解答】解:如图,
∵AB∥DE,BC∥EF,
∴∠B=∠CGD,∠E=∠BGD,
∵∠CGD+∠BGD=180°,
∴∠B+∠E=180°,
即∠B与∠E互补.
故选:D.
3.【解答】解:∵∠5+∠2=180°,
∴a∥b,
∵a∥c,
∴b∥c,
故A符合题意;
由∠3=∠6,不能推出b∥c,
故B不符合题意;
由∠4+∠6=180°,不能推出b∥c,
故C不符合题意;
由∠1=∠2,不能推出b∥c,
故D不符合题意;
故选:A.
4.【解答】解:标出字母,如图:
∵∠3=∠2=40°,∠ACB=90°,
∴∠4=90°﹣∠3=50°,
∵DE∥FG,
∴∠1=∠4=50°.
故选:C.
5.【解答】解:过点M作ME∥AB,如图,
∵AB∥CD,
∴AB∥ME∥CD,
∴∠ABM=∠BME=30°,∠CDM=∠DME=45°,
∴∠BMD=∠BME+∠DME=75°.
故选:C.
6.【解答】解:如图,
∵AB∥CD,∠2=132°,
∴∠DMN=∠ANM=∠2=132°,
根据折叠的性质得,∠1=∠DME,∠DMN=∠1+∠MDE,
∴2∠1=132°,
解得:∠1=66°.
故选:B.
7.【解答】解:∵AB∥DE∥CF,∠ABC=70°,∠CDE=130°,
∴∠BCF=∠ABC=70°,∠DCF=180°﹣∠CDE=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°,
故选:B.
二.填空题
8.【解答】解:如图:
∵AB∥CD,
∴∠2=∠3=70°,
∴∠1=180°﹣∠3=110°,
故答案为:110°.
9.【解答】解:∵AD∥CB,
∴∠ADF=∠CBD,
∵∠EDA+∠ADF=180°,
∴∠ADF=180°﹣∠EDA=180°﹣128°=52°,
∴∠CBD=52°.
故答案为:52.
10.【解答】解:过B作BD∥AE,
∵AE∥CF,
∴BD∥CF,
∴∠A=∠ABD=70°,∠DBC+∠C=180°,
∵∠C=161°,
∴∠DBC=19°,
则∠ABC=∠ABD+∠DBC=89°.
故答案为:89°.
11.【解答】解:如图,当点M在线段AD上时,
过点M作ME∥AB,
∴∠AME=∠BAD=40°,
∵ME∥AB,AB∥CD,
∴ME∥CD,
∴∠EMN+∠MNC=180°,
∵∠MNC=α,
∴∠EMN=180°﹣α,
∴∠AMN=∠AME+∠EMN=40°+(180°﹣α)=220°﹣α;
如图,当点M在AD的延长线上时,
过点M作ME∥AB,
∴∠AME=∠BAD=40°,
∵ME∥AB,AB∥CD,
∴ME∥CD,
∴∠EMN+∠MNC=180°,
∵∠MNC=α,
∴∠EMN=180°﹣α,
∴∠AMN=∠AME﹣∠EMN=40°﹣(180°﹣α)=α﹣140°;
如图,当点M在DA的延长线上时,
过点M作ME∥AB,
∴∠AME=∠BAD=40°,
∵ME∥AB,AB∥CD,
∴ME∥CD,
∴∠EMN=∠MNC=α,
∴∠AMN=∠EMN﹣∠AME=α﹣40°;
故答案为:220°﹣α或α﹣140°或α﹣40°.
12.【解答】解:如图,过点B作l3∥l2,则∠2=∠1=43°,
∵BC与l2,
∴∠4=90°,
∵直线l1∥l2,
∴l1∥l3,
∴∠3=∠4=90°,
∴∠ABC=∠3+∠2=90°+43°=133°.
故答案为:133°.
13.【解答】解:∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,故①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,故②正确;
∵BC∥AD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90°﹣45°=45°,故③错误;
∵∠D=30°,∠CAD=150°,
∴∠CAD+∠D=180°,
∴AC∥DE,
∴∠4=∠C,故④正确.
故答案为:①②④.
14.【解答】解:γ+α=90°+β.理由如下:
作PF∥AB,如图,
可得∠ABE+∠EFP=∠BEF,
而∠PFC=∠FCD,
∴∠EFP=90°﹣α,∠PFC=β,
∴∠EFP+∠PFC=90°﹣α+β,
∴γ=90°﹣α+β,
即γ+α=90°+β.
故答案为:γ+α=90°+β.
三.解答题
15.【解答】解:∵∠BAM=75°,∠BGE=75°,
∴∠BAM=∠BGE(等量代换).
∴AM∥EF(同位角相等,两直线平行).
∴∠AGH=∠BAM=75°(两直线平行,内错角相等).
∵∠CHG=105°,
∴∠AGH+∠CHG=75°+105°=180°(角度计算).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:等量代换;AM;EF;同位角相等,两直线平行;两直线平行,内错角相等;角度计算;AB;CD;同旁内角互补,两直线平行.
16.【解答】证明:∵EF∥AB,
∴∠F=∠BDF,
又∵∠A=∠F,
∴∠A=∠BDF,
∴DF∥AC.
17.【解答】证明:∵CD平分∠ACB(已知),
∴∠ACD=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠ACD=∠CDE (两直线平行,内错角相等),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(角平分线的定义).
故答案为:∠DCE;∠CDE;两直线平行,内错角相等;∠DEF;两直线平行,内错角相等;∠FEB;两直线平行,同位角相等;∠DEF;∠FEB.
18.【解答】(1)证明:∵BD⊥AC,EF⊥AC,
∴∠3=∠4=90°,
∵∠1+∠C=90°,
∴∠CDG+∠C=∠1+∠3+∠C=180°,
∴DG∥BC;
(2)解:∵∠3=90°,∠C=50°,
∴∠DBC=180°﹣∠3﹣∠C=40°,
∵BD平分∠ABC,
∴∠CBG=2∠DBC=80°,
∵DG∥BC,
∴∠BGD+∠CBG=180°,
∴∠BGD=100°.
19.【解答】解:过点D作DF⊥AO交OB于点F.
∵入射角等于反射角,
∴∠1=∠3,
∵CD∥OB,
∴∠1=∠2,
∴∠2=∠3,
在Rt△DOF中,∠ODF=90°,∠AOB=37°36′,
∴∠2=90°﹣37°36′=52°24′;
在△DEF中,∠DEB=180°﹣2∠2=75°12′=75.2°.
20.【解答】(1)证明:∵EF∥AC,
∴∠CAE=∠1,
∵∠1+∠2=180°,
∴∠CAE+∠2=180°,
∴AE∥DG.
(2)解:∵EF∥AC,∠C=40°,
∴∠BEF=∠C=40°,
∵EF平分∠AEB,
∴∠BEF=∠1=40°,
∴∠AEB=80°,
由(1)知AE∥DG,
∴∠BDG=∠AEB=80°.
21.【解答】解:(1)如图①,过点E作EM∥AB,
∵AB∥CD,
∴AB∥CD∥EM,
∴∠1=∠NEM,∠3=∠MEF,
∴∠1+∠3=∠NEM=∠MEF,
即∠1+∠3=∠2;
(2)如图②,过点F作NF∥AB,
∵AB∥CD,
∴AB∥CD∥FN,
∴∠4=∠NFH,
由(1)知,∠1+∠EFN=∠2,
∴∠1+∠EFN+∠NFH=∠2+∠4,
即∠1+∠3=∠2+∠4;
(3)如图③,过点G作GM∥AB,
∵AB∥CD,
∴AB∥CD∥GM,
∴∠5=∠MGN,
由(2)得,∠1+∠3=∠2+∠FGM,
∴∠1+∠3+∠5=∠2+∠FGM+∠MGN,
即∠1+∠3+∠5=∠2+∠4.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
