第一章《平行线的性质》基础选择题(含解析)
文档属性
| 名称 | 第一章《平行线的性质》基础选择题(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 234.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-09 20:24:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
平行线的性质(选择题基础题)
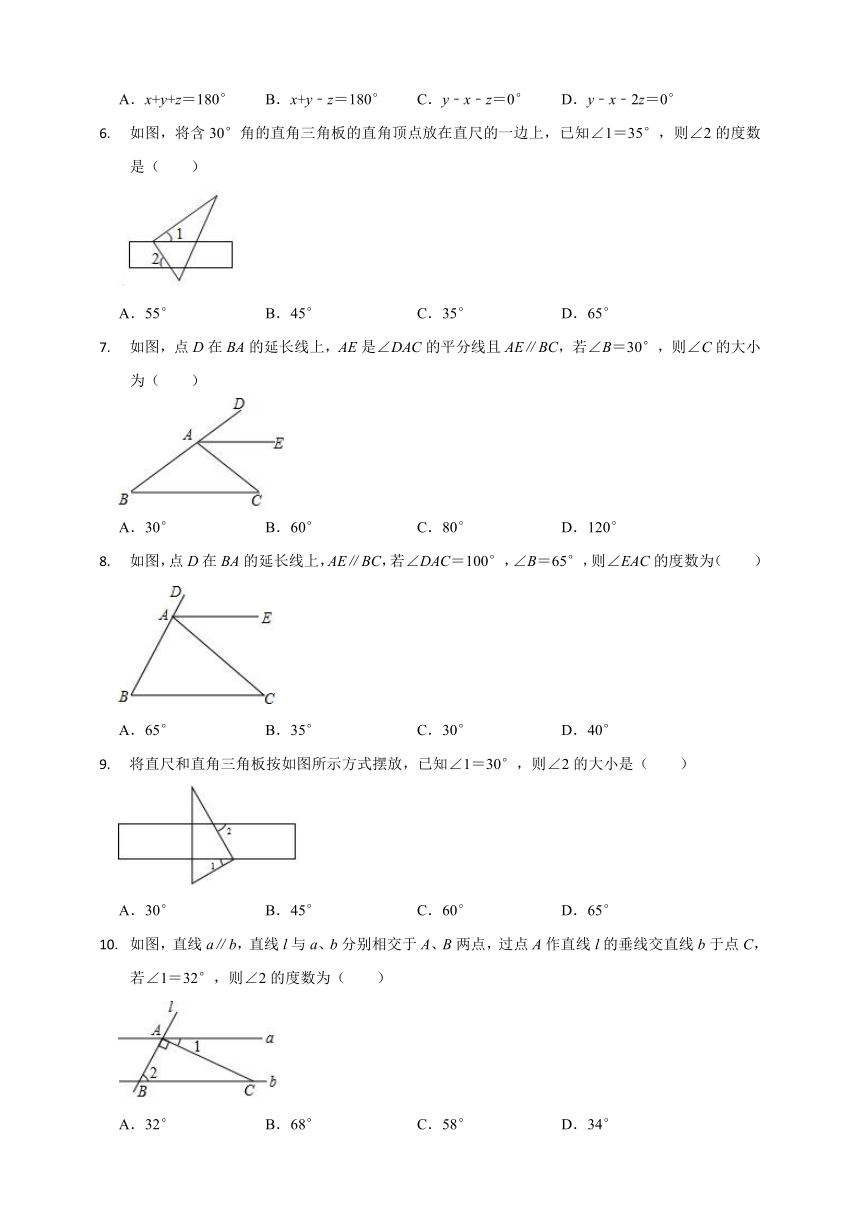
如图,直线a∥b,将三角板的直角顶点放在直线b上,如果∠1=40°,则∠2的度数是( )
A.30° B.40° C.45° D.50°
将一张长方形纸条折成如图所示的形状,BC为折痕.若∠DBA=70°,则∠ABC等于( )
A.45° B.55° C.70° D.110°
光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,当∠1=45°,∠2=122°时,∠3和∠4的度数分别是( )
A.58°,122° B.45°,68° C.45°,58° D.45°,45°
如图,已知AF是∠BAC的平分线,点D在AB上,过点D作DG∥AC交AF于点E.如果∠DEA=28°,那么∠BDG的度数为( )
A.28° B.56° C.58° D.84°
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
A.x+y+z=180° B.x+y﹣z=180° C.y﹣x﹣z=0° D.y﹣x﹣2z=0°
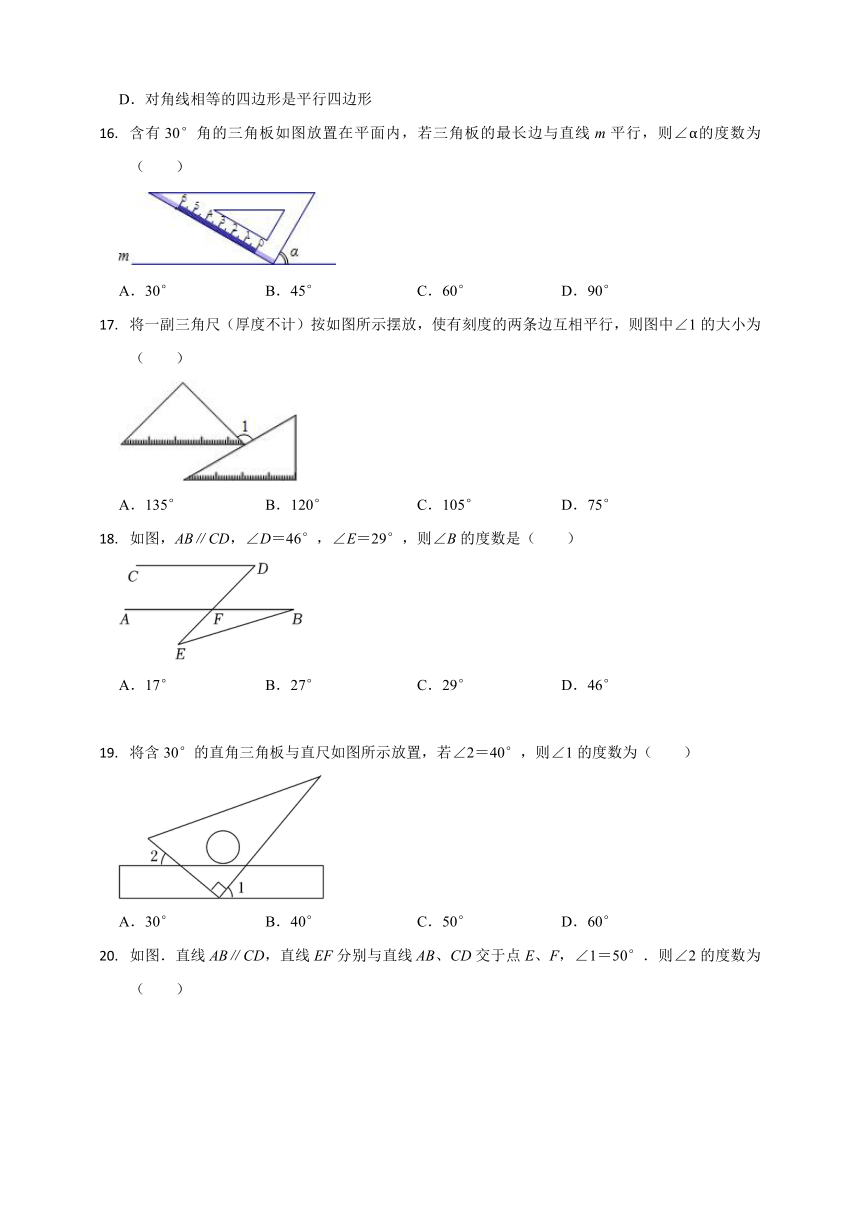
如图,将含30°角的直角三角板的直角顶点放在直尺的一边上,已知∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.65°
如图,点D在BA的延长线上,AE是∠DAC的平分线且AE∥BC,若∠B=30°,则∠C的大小为( )
A.30° B.60° C.80° D.120°
如图,点D在BA的延长线上,AE∥BC,若∠DAC=100°,∠B=65°,则∠EAC的度数为( )
A.65° B.35° C.30° D.40°
将直尺和直角三角板按如图所示方式摆放,已知∠1=30°,则∠2的大小是( )
A.30° B.45° C.60° D.65°
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=32°,则∠2的度数为( )
A.32° B.68° C.58° D.34°
如图,点F是∠ACE内一点,FD∥AC,FB∥EC,点D在射线CE上,点B在射线CA上.下列结论正确的是( )
①∠1=∠F;
②∠2=∠C;
③∠FBC=∠FDC;
④∠FBC+∠2=180°.
A.①② B.①②④ C.①②③ D.①②③④
如图,AB∥CD,AD⊥CE于点A,∠1=60°,则∠2的度数是( )
A.30° B.40° C.45° D.60°
如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,则∠2等于( )
A.35° B.50° C.55° D.65°
在同一平面内,下列说法中,错误的是( )
A.过两点有且只有一条直线
B.过一点有无数条直线与已知直线平行
C.过直线外一点有且只有一条直线与已知直线平行
D.平面内,过一点有且只有一条直线与已知直线垂直
下列命题中是真命题的是( )
A.同位角相等
B.有两边及一角分别相等的两个三角形全等
C.两组对边分别相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
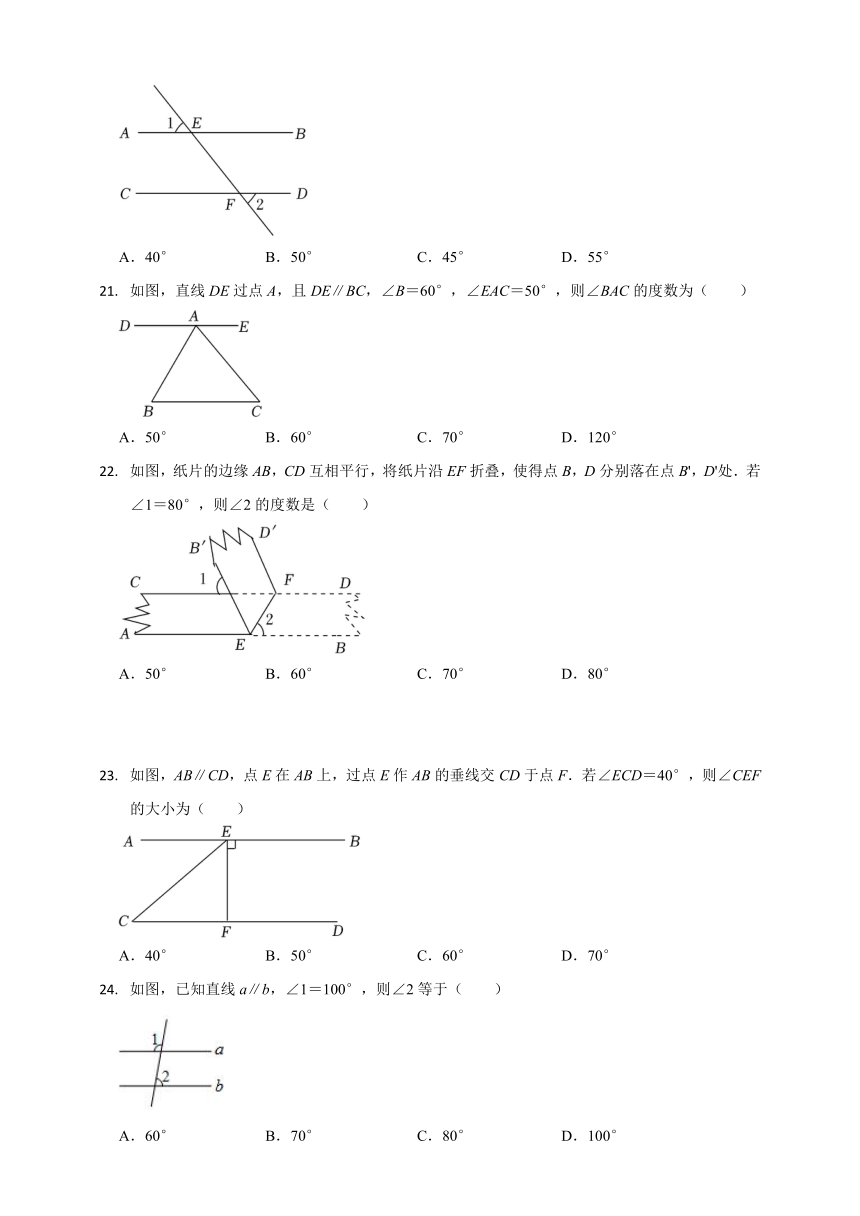
含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )
A.30° B.45° C.60° D.90°
将一副三角尺(厚度不计)按如图所示摆放,使有刻度的两条边互相平行,则图中∠1的大小为( )
A.135° B.120° C.105° D.75°
如图,AB∥CD,∠D=46°,∠E=29°,则∠B的度数是( )
A.17° B.27° C.29° D.46°
将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )
A.30° B.40° C.50° D.60°
如图.直线AB∥CD,直线EF分别与直线AB、CD交于点E、F,∠1=50°.则∠2的度数为( )
A.40° B.50° C.45° D.55°
如图,直线DE过点A,且DE∥BC,∠B=60°,∠EAC=50°,则∠BAC的度数为( )
A.50° B.60° C.70° D.120°
如图,纸片的边缘AB,CD互相平行,将纸片沿EF折叠,使得点B,D分别落在点B',D'处.若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
如图,AB∥CD,点E在AB上,过点E作AB的垂线交CD于点F.若∠ECD=40°,则∠CEF的大小为( )
A.40° B.50° C.60° D.70°
如图,已知直线a∥b,∠1=100°,则∠2等于( )
A.60° B.70° C.80° D.100°
如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
(2022春 通州区期末)如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
A.70° B.100° C.110° D.120°
参考答案与试题解析
【解析】解:∵直线a∥b,
∴∠1=∠3,
∵∠1=40°,
∴∠3=40°,
∵三角板的直角顶点放在直线b上,
∴∠3+∠2=90°,
∴∠2=50°,
【答案】D.
【解析】解:根据题意,得:2∠ABC+∠DBA=180°,
则∠ABC=(180°﹣70°)÷2=55°.
【答案】B.
【解析】解:∵EG∥FH,∠1=45°,
∴∠3=∠1=45°.
∵AB∥CD,∠2=122°,
∴∠ECD=180°﹣122°=58°.
∵CE∥DF,
∴∠4=∠ECD=58°.
【答案】C.
【解析】解:∵DG∥AC,
∴∠EAC=∠DEA=28°.
∵AF是∠BAC的平分线,
∴∠DAE=∠EAC=28°.
∴∠BDG=∠DAE+∠DEA
=28°+28°
=56°.
【答案】B.
【解析】解:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°﹣y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°﹣y,
∴x+y﹣z=180°,
【答案】B.
【解析】解:如图,∵∠CAE=90°,∠1=35°,
∴∠BAC=90°﹣35°=55°,
∵AB∥CD,
∴∠2=∠BAC=55°,
【答案】A.
【解析】解:∵AE∥BC,∠B=30°,
∴∠DAE=30°,
∵AE是∠DAC的平分线,
∴∠CAE=30°,
∴∠C=30°.
【答案】A.
【解析】解:∵AE∥BC,
∴∠B=∠DAE=65°,
又∵∠DAC=100°,
∴∠EAC=∠DAC﹣∠DAE=100°﹣65°=35°,
【答案】B.
【解析】解:如图,
∵∠ACB=90°,∠1=30°,
∴∠ACE=90°﹣30°=60°,
∵MN∥EF,
∴∠2=∠ACE=60°.
【答案】C.
【解析】解:∵直线a∥b,
∴∠2+∠BAC+∠1=180°,
∵AC⊥BA,
∴∠BAC=90°,
∴∠2=180°﹣∠1﹣∠BAC=180°﹣90°﹣32°=58°,
【答案】C.
【解析】解:①:∵FD∥AC,
∴∠1=∠F.
故①正确.
②:∵FD∥AC,
∴∠2=∠C.
故②正确.
③:∵FD∥AC,FB∥EC,
∴四边形CDFB是平行四边形.
∴∠FBC=∠FDC.
故③正确.
④:由③知:∠FBC=∠FDC.
∵∠2+∠FDC=180°,
∴∠FBC+∠2=180°.
故④正确.
综上:①②③④均正确.
【答案】D.
【解析】解:∵AD⊥CE于点A,
∴∠CAD=90°,
∵∠1=60°,
∴∠ACD=90°﹣∠1=30°,
∵AB∥CD,
∴∠2=∠ACD=30°.
【答案】A.
【解析】解:∵a∥b,∠1=35°,
∴∠BAC=∠1=35°.
∵AB⊥BC,
∴∠2=∠BCA=90°﹣∠BAC=90°﹣35°=55°.
【答案】C.
【解析】解:A、过两点有且只有一条直线,正确,不符合题意;
B、过一点有且只有一条直线与已知直线平行,原命题错误,符合题意;
C、过直线外一点有且只有一条直线与已知直线平行,正确,不符合题意;
D、平面内,过一点有且只有一条直线与已知直线垂直,正确,不符合题意.
【答案】B.
【解析】解:A、两直线平行,同位角相等,故原命题错误,是假命题,不符合题意;
B、有两边及夹角分别相等的两个三角形全等,故原命题错误,是假命题,不符合题意;
C、两组对边分别相等的四边形是平行四边形,正确,是真命题,符合题意;
D、对角线互相平分的四边形是平行四边形,故原命题错误,是假命题,不符合题意,
【答案】C.
【解析】解:∵图中是含有30°角的三角板,
∴∠β=60°,
∵三角板的最长边与直线m平行,
∴∠α=∠β=60°.
【答案】C.
【解析】解:如图:
∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵∠ABE=45°,
∴∠1=180°﹣∠ABE﹣∠ABC=105°,
【答案】C.
【解析】解:∵AB∥CD,
∴∠D=∠AFE=46°,
∴∠BFE=180°﹣∠AFE=134°,
∵∠E=29°,
∴∠B=180°﹣∠E﹣∠BFE=17°,
【答案】A.
【解析】解:标出字母,如图:
∵∠3=∠2=40°,∠ACB=90°,
∴∠4=90°﹣∠3=50°,
∵DE∥FG,
∴∠1=∠4=50°.
【答案】C.
【解析】解:∵∠BEF=∠1=50°,AB∥CD,
∴∠2=∠BEF=50°.
【答案】B.
【解析】解:∵DE∥BC,
∴∠DAB=∠B=60°,
∵∠EAC=50°,
∴∠BAC=180°﹣∠DAB﹣∠EAC=70°,
【答案】C.
【解析】解:∵AB∥CD,
∴∠1=∠AEB′=80°,
∴∠BEB′=180°﹣∠AEB′=100°,
由折叠得:
∠2=∠FEB′=∠BEB′=50°,
【答案】A.
【解析】解:∵过点E作AB的垂线交CD于点F,
∴∠AEF=90°,
∵AB∥CD,∠ECD=40°,
∴∠AEC=∠ECD=40°,
∴∠CEF=∠AEF﹣∠AEC=50°.
【答案】B.
【解析】解:∵a∥b,∠1=100°,
∴∠3=100°,
∴∠2=80°,
【答案】C.
【解析】解:∵DE∥BC,
∴∠DAB=∠B=60°,
∴∠2=180°﹣∠DAB﹣∠1=180°﹣60°﹣50°=70°.
【答案】C.
【解析】解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠1=180°﹣70°=110°.
【答案】C.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
平行线的性质(选择题基础题)
如图,直线a∥b,将三角板的直角顶点放在直线b上,如果∠1=40°,则∠2的度数是( )
A.30° B.40° C.45° D.50°
将一张长方形纸条折成如图所示的形状,BC为折痕.若∠DBA=70°,则∠ABC等于( )
A.45° B.55° C.70° D.110°
光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,当∠1=45°,∠2=122°时,∠3和∠4的度数分别是( )
A.58°,122° B.45°,68° C.45°,58° D.45°,45°
如图,已知AF是∠BAC的平分线,点D在AB上,过点D作DG∥AC交AF于点E.如果∠DEA=28°,那么∠BDG的度数为( )
A.28° B.56° C.58° D.84°
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
A.x+y+z=180° B.x+y﹣z=180° C.y﹣x﹣z=0° D.y﹣x﹣2z=0°
如图,将含30°角的直角三角板的直角顶点放在直尺的一边上,已知∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.65°
如图,点D在BA的延长线上,AE是∠DAC的平分线且AE∥BC,若∠B=30°,则∠C的大小为( )
A.30° B.60° C.80° D.120°
如图,点D在BA的延长线上,AE∥BC,若∠DAC=100°,∠B=65°,则∠EAC的度数为( )
A.65° B.35° C.30° D.40°
将直尺和直角三角板按如图所示方式摆放,已知∠1=30°,则∠2的大小是( )
A.30° B.45° C.60° D.65°
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=32°,则∠2的度数为( )
A.32° B.68° C.58° D.34°
如图,点F是∠ACE内一点,FD∥AC,FB∥EC,点D在射线CE上,点B在射线CA上.下列结论正确的是( )
①∠1=∠F;
②∠2=∠C;
③∠FBC=∠FDC;
④∠FBC+∠2=180°.
A.①② B.①②④ C.①②③ D.①②③④
如图,AB∥CD,AD⊥CE于点A,∠1=60°,则∠2的度数是( )
A.30° B.40° C.45° D.60°
如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,则∠2等于( )
A.35° B.50° C.55° D.65°
在同一平面内,下列说法中,错误的是( )
A.过两点有且只有一条直线
B.过一点有无数条直线与已知直线平行
C.过直线外一点有且只有一条直线与已知直线平行
D.平面内,过一点有且只有一条直线与已知直线垂直
下列命题中是真命题的是( )
A.同位角相等
B.有两边及一角分别相等的两个三角形全等
C.两组对边分别相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )
A.30° B.45° C.60° D.90°
将一副三角尺(厚度不计)按如图所示摆放,使有刻度的两条边互相平行,则图中∠1的大小为( )
A.135° B.120° C.105° D.75°
如图,AB∥CD,∠D=46°,∠E=29°,则∠B的度数是( )
A.17° B.27° C.29° D.46°
将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )
A.30° B.40° C.50° D.60°
如图.直线AB∥CD,直线EF分别与直线AB、CD交于点E、F,∠1=50°.则∠2的度数为( )
A.40° B.50° C.45° D.55°
如图,直线DE过点A,且DE∥BC,∠B=60°,∠EAC=50°,则∠BAC的度数为( )
A.50° B.60° C.70° D.120°
如图,纸片的边缘AB,CD互相平行,将纸片沿EF折叠,使得点B,D分别落在点B',D'处.若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
如图,AB∥CD,点E在AB上,过点E作AB的垂线交CD于点F.若∠ECD=40°,则∠CEF的大小为( )
A.40° B.50° C.60° D.70°
如图,已知直线a∥b,∠1=100°,则∠2等于( )
A.60° B.70° C.80° D.100°
如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
(2022春 通州区期末)如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
A.70° B.100° C.110° D.120°
参考答案与试题解析
【解析】解:∵直线a∥b,
∴∠1=∠3,
∵∠1=40°,
∴∠3=40°,
∵三角板的直角顶点放在直线b上,
∴∠3+∠2=90°,
∴∠2=50°,
【答案】D.
【解析】解:根据题意,得:2∠ABC+∠DBA=180°,
则∠ABC=(180°﹣70°)÷2=55°.
【答案】B.
【解析】解:∵EG∥FH,∠1=45°,
∴∠3=∠1=45°.
∵AB∥CD,∠2=122°,
∴∠ECD=180°﹣122°=58°.
∵CE∥DF,
∴∠4=∠ECD=58°.
【答案】C.
【解析】解:∵DG∥AC,
∴∠EAC=∠DEA=28°.
∵AF是∠BAC的平分线,
∴∠DAE=∠EAC=28°.
∴∠BDG=∠DAE+∠DEA
=28°+28°
=56°.
【答案】B.
【解析】解:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°﹣y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°﹣y,
∴x+y﹣z=180°,
【答案】B.
【解析】解:如图,∵∠CAE=90°,∠1=35°,
∴∠BAC=90°﹣35°=55°,
∵AB∥CD,
∴∠2=∠BAC=55°,
【答案】A.
【解析】解:∵AE∥BC,∠B=30°,
∴∠DAE=30°,
∵AE是∠DAC的平分线,
∴∠CAE=30°,
∴∠C=30°.
【答案】A.
【解析】解:∵AE∥BC,
∴∠B=∠DAE=65°,
又∵∠DAC=100°,
∴∠EAC=∠DAC﹣∠DAE=100°﹣65°=35°,
【答案】B.
【解析】解:如图,
∵∠ACB=90°,∠1=30°,
∴∠ACE=90°﹣30°=60°,
∵MN∥EF,
∴∠2=∠ACE=60°.
【答案】C.
【解析】解:∵直线a∥b,
∴∠2+∠BAC+∠1=180°,
∵AC⊥BA,
∴∠BAC=90°,
∴∠2=180°﹣∠1﹣∠BAC=180°﹣90°﹣32°=58°,
【答案】C.
【解析】解:①:∵FD∥AC,
∴∠1=∠F.
故①正确.
②:∵FD∥AC,
∴∠2=∠C.
故②正确.
③:∵FD∥AC,FB∥EC,
∴四边形CDFB是平行四边形.
∴∠FBC=∠FDC.
故③正确.
④:由③知:∠FBC=∠FDC.
∵∠2+∠FDC=180°,
∴∠FBC+∠2=180°.
故④正确.
综上:①②③④均正确.
【答案】D.
【解析】解:∵AD⊥CE于点A,
∴∠CAD=90°,
∵∠1=60°,
∴∠ACD=90°﹣∠1=30°,
∵AB∥CD,
∴∠2=∠ACD=30°.
【答案】A.
【解析】解:∵a∥b,∠1=35°,
∴∠BAC=∠1=35°.
∵AB⊥BC,
∴∠2=∠BCA=90°﹣∠BAC=90°﹣35°=55°.
【答案】C.
【解析】解:A、过两点有且只有一条直线,正确,不符合题意;
B、过一点有且只有一条直线与已知直线平行,原命题错误,符合题意;
C、过直线外一点有且只有一条直线与已知直线平行,正确,不符合题意;
D、平面内,过一点有且只有一条直线与已知直线垂直,正确,不符合题意.
【答案】B.
【解析】解:A、两直线平行,同位角相等,故原命题错误,是假命题,不符合题意;
B、有两边及夹角分别相等的两个三角形全等,故原命题错误,是假命题,不符合题意;
C、两组对边分别相等的四边形是平行四边形,正确,是真命题,符合题意;
D、对角线互相平分的四边形是平行四边形,故原命题错误,是假命题,不符合题意,
【答案】C.
【解析】解:∵图中是含有30°角的三角板,
∴∠β=60°,
∵三角板的最长边与直线m平行,
∴∠α=∠β=60°.
【答案】C.
【解析】解:如图:
∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵∠ABE=45°,
∴∠1=180°﹣∠ABE﹣∠ABC=105°,
【答案】C.
【解析】解:∵AB∥CD,
∴∠D=∠AFE=46°,
∴∠BFE=180°﹣∠AFE=134°,
∵∠E=29°,
∴∠B=180°﹣∠E﹣∠BFE=17°,
【答案】A.
【解析】解:标出字母,如图:
∵∠3=∠2=40°,∠ACB=90°,
∴∠4=90°﹣∠3=50°,
∵DE∥FG,
∴∠1=∠4=50°.
【答案】C.
【解析】解:∵∠BEF=∠1=50°,AB∥CD,
∴∠2=∠BEF=50°.
【答案】B.
【解析】解:∵DE∥BC,
∴∠DAB=∠B=60°,
∵∠EAC=50°,
∴∠BAC=180°﹣∠DAB﹣∠EAC=70°,
【答案】C.
【解析】解:∵AB∥CD,
∴∠1=∠AEB′=80°,
∴∠BEB′=180°﹣∠AEB′=100°,
由折叠得:
∠2=∠FEB′=∠BEB′=50°,
【答案】A.
【解析】解:∵过点E作AB的垂线交CD于点F,
∴∠AEF=90°,
∵AB∥CD,∠ECD=40°,
∴∠AEC=∠ECD=40°,
∴∠CEF=∠AEF﹣∠AEC=50°.
【答案】B.
【解析】解:∵a∥b,∠1=100°,
∴∠3=100°,
∴∠2=80°,
【答案】C.
【解析】解:∵DE∥BC,
∴∠DAB=∠B=60°,
∴∠2=180°﹣∠DAB﹣∠1=180°﹣60°﹣50°=70°.
【答案】C.
【解析】解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠1=180°﹣70°=110°.
【答案】C.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
