七下数学第三章3.5整式的化简

(共18张PPT)
复习引入
(am)n=
amn
(ab)n=
anbn
M
P
F
E
D
C
B
A
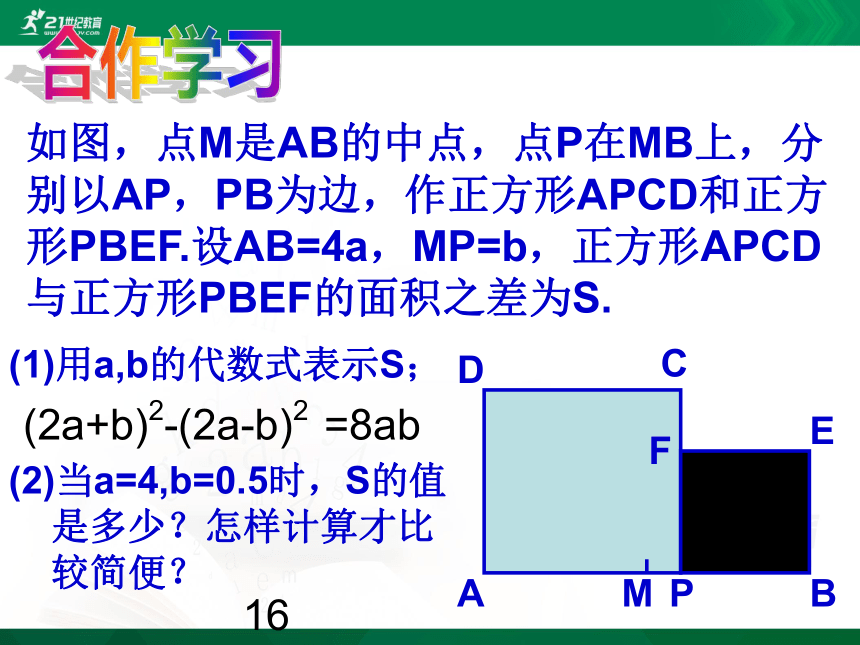
如图，点M是AB的中点，点P在MB上，分
别以AP，PB为边，作正方形APCD和正方
形PBEF.设AB=4a，MP=b，正方形APCD
与正方形PBEF的面积之差为S.
(1)用a,b的代数式表示S；
(2)当a=4,b=0.5时，S的值
是多少？怎样计算才比
较简便？
(2a+b)2-(2a-b)2
=8ab
16
整式的化简应遵循先乘方、再乘除、
最后算加减的顺序。
能运用乘法公式的则运用公式。
例1 化简：
（1）（2x－1）（2x＋1）－（4x＋3）（x－6）
（2）（2a＋3b）2－4a（a＋3b＋1）
解：（1）原式=
4x2 －1 －
=4x2 －1 －(4x2 －21x －18)
=4x2 －1 －4x2 +21x +18
=21x +17
（2）原式=
4a2+12ab+9b2
=9b2 －4a
(4x2 －24x+3x －18)
－4a2 － 12ab － 4a
（1）先观察所要化简的整式，其中含有哪
些运算？确定运算的顺序。
（2）各种运算应遵循怎样的运算法则？乘法
公式是否适用？
（3）结果的形式应保持最简，有同类项的必须
合并同类项。
注意：
(1) (x+6)2-(3+x)(3-x)
(2) 3x(x2+3x+8)+(-3x-4)(3x-4)
(3) (2x-5y)(2x+5y)-(2x+y)2
(1)2x2+12x+27 (2)3x3+24x+16 (3)-26y2-4xy
一块手表原价100元，降价10％，
则现价为_____元。
90
2. 一块手表原价a元，降价x％，则
现价为_______元。
a(1-x％)
3. 一块手表原价a(1-x％)元，降价x％，则现价为_________元。
a(1-x％)2
1. 一块手表原价a元，涨价x％，则
现价为_________元。
a(1+x％)
2. 一块手表原价a元，连续两次涨价
x％，则现价为_________元。
a(1+x％)2
例2 甲、乙两家超市3月份的销售额均为a万元，在4月和5月这两个月中，甲超市的销售额平均每月增长x%，而乙超市的销售额平均每月减少x%。
（1）5月份甲超市的销售额比乙超市多多少？
（2）如果a=150，x=2，那么5月份甲超市的销售额比乙超市多多少万元？
上海家乐福超市
实际应用
3月份
4月份
5月份
甲超市
销售额
乙超市
销售额
a
a
a(1＋x%)
a(1－x%)
a(1＋x%) (1＋x%)
= a(1＋x%)2
a(1－x%) (1－x%)
= a(1－x%)2
太好了！我们一起努力。
例2 甲、乙两家超市3月份的销售额均为a万元，在4月和5月这两个月中，甲超市的销售额平均每月增长x%，而乙超市的
销售额平均每月减少x%。
（1）5月份甲超市的销售额比乙超市多多少？
3月份
4月份
5月份
甲超市
销售额
乙超市
销售额
a
a
a(1＋x%)
a(1＋x%) (1＋x%)
= a(1＋x%)2
a(1－x%) (1－x%)
= a(1－x%)2
a(1－x%)
差额为：
a(1＋x%)2－a(1－x%)2
=a(1＋——＋—— )
2x
100
10000
x2
= ——(万元)
25
ax
解：当a=150，x=2时，
—— = ———
25
ax
=12（万元）
25
150×2
要加油啊！
100
10000
－a(1 －——＋—— )
2x
x2
（2）如果a=150，x=2，那么5月份甲超市的销售额
比乙超市多多少万元？
2、有两个圆，较大圆的半径为r(mm)，较小圆
的半径比r小3(mm)，求两圆的面积之差.当
r=10mm时，面积之差是多少？当r=15mm
时呢？
1、当
时，求代数式
的值
练一练
已知x+y=3，xy=1，求x2+y2与(x-y)2的值.
x2+y2=(x+y) 2-2xy=32-2=7
(x-y) 2=(x+y) 2-2xy-2xy=32-4=5
　　1、已知 x + y =10，xy=24，
则 x2 + y2 = ;
52
2、已知 x + y =3， x2 + y2 =7，
则 xy = ;
1
观察下列各式：
52=25
152=225
252=625
352=1225
……
　
小组合作,
探究推理
你能口算末位数是
5的两位数的平方吗？
试说明理由。
52=25
152=225
252=625
352=1225
452=2025
……
752=5625
852=7225
可写成 ＋25
可写成 ＋25
可写成 ＋25
可写成 ＋25
可写成 ＋25
……
可写成
可写成
100×1×（1＋1）
100×2×（2＋1）
100×3×（3＋1）
100×4×（4＋1）
（1）探索规律：
100×0×（0＋1）
（2）归纳、猜想 ：
（3）根据上面的归纳、猜想，试计算：
20052= 。
100×7×8＋25
100×8×9＋25
4020025
真厉害！
（10n＋5）2= 100n2+100n+25= 100ｎ(ｎ+１)+25
一、你能说出这节课的收获吗？
二、应用整式解决实际问题的基本过程：
列代数式 化简 求值