2022-2023学年浙教版七年级数学下册第1章平行线基础练习卷(含答案)
文档属性
| 名称 | 2022-2023学年浙教版七年级数学下册第1章平行线基础练习卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 22:40:18 | ||
图片预览




文档简介
第1章平行线基础练习卷2022-2023学年浙教版七年级数学下册
一、单选题
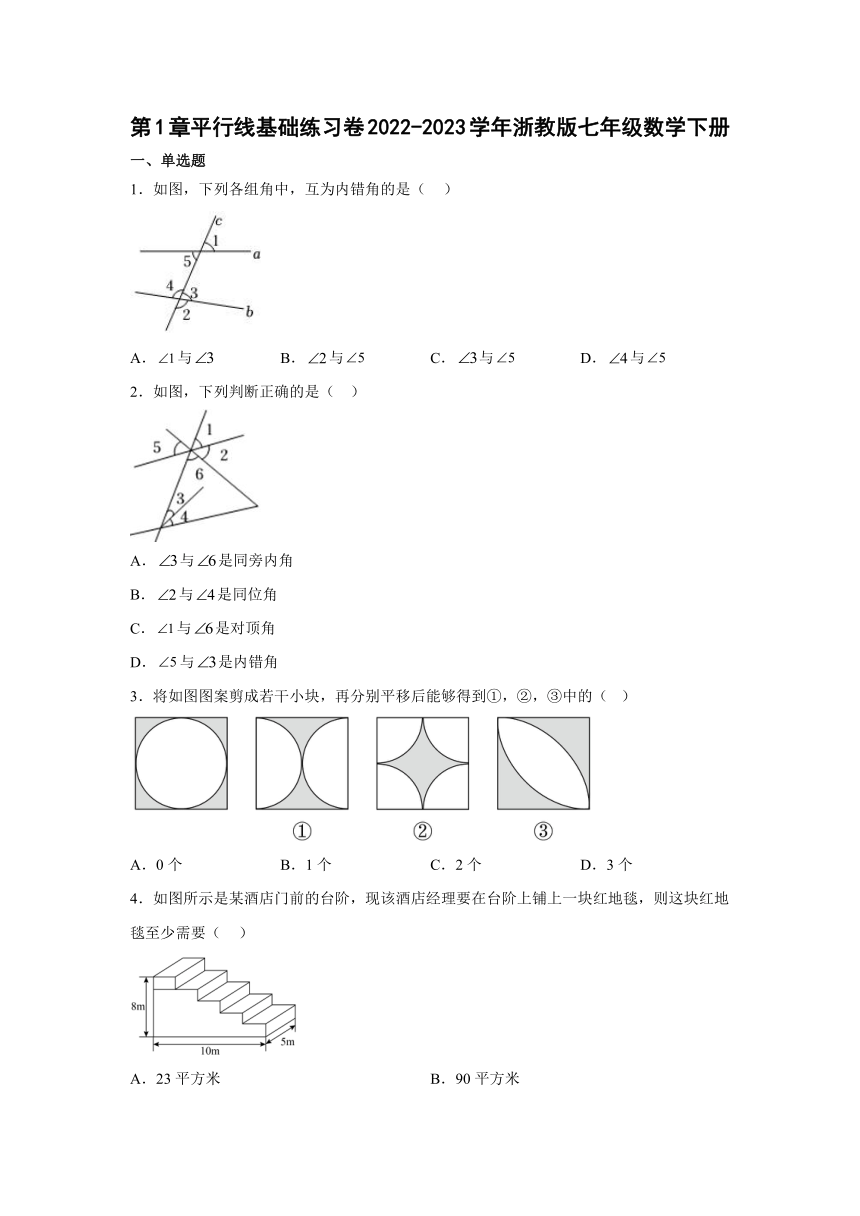
1.如图,下列各组角中,互为内错角的是( )
A.与 B.与 C.与 D.与
2.如图,下列判断正确的是( )
A.与是同旁内角
B.与是同位角
C.与是对顶角
D.与是内错角
3.将如图图案剪成若干小块,再分别平移后能够得到①,②,③中的( )
A.0个 B.1个 C.2个 D.3个
4.如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,则这块红地毯至少需要( )
A.23平方米 B.90平方米
C.130平方米 D.120平方米
5.如图,将一直角三角板与两边平行的纸条,如图所示放置,下列结论(1);(2);(3);(4),其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6.2022年北京冬奥会男子500米短道速滑冠军高亭玉在一次速滑训练中,经过两次拐弯后的速滑方向与原来的方向相反,则两次拐弯的角度可能是( )
A.第一次向左拐52°,第二次向右拐52° B.第一次向左拐48°,第二次向左拐48°
C.第一次向左拐73°,第二次向右拐107° D.第一次向左拐32°,第二次向左拐148°
7.如图,直线,于点C,,则的度数为( )
A. B. C. D.
8.如图,将一副三角板按如图放置,则下列结论:①;②;③如果,则有;④.其中正确的序号是( )
A.①②③④ B.①②④ C.①②③ D.①③④
9.如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
10.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为6,则△BCE的面积为( )
A.5 B.6 C.10 D.3
11.如图,下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
12.如图,要添加一个条件使AB∥CD,则下列选项中正确的是( )
A.∠A=∠DCE B.∠B=∠DCE C.∠A=∠B D.∠BCE=∠A+∠B
13.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
14.下列说法中是真命题正确的个数有( )个
(1)若ab,bd,则ad;(2)过一点有且只有一条直线与已知直线平行;(3)两条直线不相交就平行;(4)过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
15.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
二、填空题
16.如图,直线a,b被直线c所截,则形成的角中与∠1互为内错角的是______.
17.如图,在正方体中,与线段AB平行的线段有____条.
18.如图,直线a与∠AOB的一边射线OA相交,∠1=130°,向下平移直线a得到直线b,与∠AOB的另一边射线OB相交,则∠2+∠3=___.
19.如图,已知直线,将一块三角板的直角顶点放在直线a上,如果,那么______度.
20.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB//DC的条件为_______.
三、解答题
21.如图,点E、F分别在AB、CD上,于点O,,,求证:.
证明:∵(已知),
∴(___________)
又∵(已知),
∴___________(___________),
∴(___________),
∴(___________),
又∵(平角的定义)
∴(___________)°,
又∵(已知),
∴(___________),
∴.(___________)
22.如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
23.两条直线被第三条直线所截,和是同旁内角,和是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若、,求,的度数
24.如图,在6×6的正方形网格中,每个小正方形的边长是1,点M、N、P、Q均为格点(格点是指每个小正方形的顶点),线段MN经过点P.
(1)过点P画线段AB,使得线段AB满足以下两个条件:①AB⊥MN;②;
(2)过点Q画MN的平行线CD,CD与AB相交于点E;
(3)若格点F使得△PFM的面积等于4,则这样的点F共有 个。
参考答案
1--10CACBD DBBCD 11---15DACAB
16.∠4
17.3
18.
19.
20.①③④
21.证明:∵(已知)
∴(垂直的定义)
又∵(已知)
∴(同位角相等,两直线平行)
∴(两直线平行,同位角相等)
∴(等量代换)
又∵(平角的定义)
∴(90)°
又∵(已知)
∴(等式的性质)
∴(内错角相等,两直线平行)
故答案为:垂直的定义;;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;90;等式的性质;内错角相等,两直线平行.
22.(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
23.解:(1)如图,下图为所求作.
(2),,
,
又,
,
,
,.
24.(1)解:作图如下:
(2)解:作图见(1)
(3)如图:
故符合题意的点F有6个.
故答案为:6
一、单选题
1.如图,下列各组角中,互为内错角的是( )
A.与 B.与 C.与 D.与
2.如图,下列判断正确的是( )
A.与是同旁内角
B.与是同位角
C.与是对顶角
D.与是内错角
3.将如图图案剪成若干小块,再分别平移后能够得到①,②,③中的( )
A.0个 B.1个 C.2个 D.3个
4.如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,则这块红地毯至少需要( )
A.23平方米 B.90平方米
C.130平方米 D.120平方米
5.如图,将一直角三角板与两边平行的纸条,如图所示放置,下列结论(1);(2);(3);(4),其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6.2022年北京冬奥会男子500米短道速滑冠军高亭玉在一次速滑训练中,经过两次拐弯后的速滑方向与原来的方向相反,则两次拐弯的角度可能是( )
A.第一次向左拐52°,第二次向右拐52° B.第一次向左拐48°,第二次向左拐48°
C.第一次向左拐73°,第二次向右拐107° D.第一次向左拐32°,第二次向左拐148°
7.如图,直线,于点C,,则的度数为( )
A. B. C. D.
8.如图,将一副三角板按如图放置,则下列结论:①;②;③如果,则有;④.其中正确的序号是( )
A.①②③④ B.①②④ C.①②③ D.①③④
9.如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
10.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为6,则△BCE的面积为( )
A.5 B.6 C.10 D.3
11.如图,下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
12.如图,要添加一个条件使AB∥CD,则下列选项中正确的是( )
A.∠A=∠DCE B.∠B=∠DCE C.∠A=∠B D.∠BCE=∠A+∠B
13.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
14.下列说法中是真命题正确的个数有( )个
(1)若ab,bd,则ad;(2)过一点有且只有一条直线与已知直线平行;(3)两条直线不相交就平行;(4)过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
15.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
二、填空题
16.如图,直线a,b被直线c所截,则形成的角中与∠1互为内错角的是______.
17.如图,在正方体中,与线段AB平行的线段有____条.
18.如图,直线a与∠AOB的一边射线OA相交,∠1=130°,向下平移直线a得到直线b,与∠AOB的另一边射线OB相交,则∠2+∠3=___.
19.如图,已知直线,将一块三角板的直角顶点放在直线a上,如果,那么______度.
20.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB//DC的条件为_______.
三、解答题
21.如图,点E、F分别在AB、CD上,于点O,,,求证:.
证明:∵(已知),
∴(___________)
又∵(已知),
∴___________(___________),
∴(___________),
∴(___________),
又∵(平角的定义)
∴(___________)°,
又∵(已知),
∴(___________),
∴.(___________)
22.如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
23.两条直线被第三条直线所截,和是同旁内角,和是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若、,求,的度数
24.如图,在6×6的正方形网格中,每个小正方形的边长是1,点M、N、P、Q均为格点(格点是指每个小正方形的顶点),线段MN经过点P.
(1)过点P画线段AB,使得线段AB满足以下两个条件:①AB⊥MN;②;
(2)过点Q画MN的平行线CD,CD与AB相交于点E;
(3)若格点F使得△PFM的面积等于4,则这样的点F共有 个。
参考答案
1--10CACBD DBBCD 11---15DACAB
16.∠4
17.3
18.
19.
20.①③④
21.证明:∵(已知)
∴(垂直的定义)
又∵(已知)
∴(同位角相等,两直线平行)
∴(两直线平行,同位角相等)
∴(等量代换)
又∵(平角的定义)
∴(90)°
又∵(已知)
∴(等式的性质)
∴(内错角相等,两直线平行)
故答案为:垂直的定义;;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;90;等式的性质;内错角相等,两直线平行.
22.(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
23.解:(1)如图,下图为所求作.
(2),,
,
又,
,
,
,.
24.(1)解:作图如下:
(2)解:作图见(1)
(3)如图:
故符合题意的点F有6个.
故答案为:6
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
