2023年浙教版七年级数学下册 第1章 平行线 单元检测卷(含解析)
文档属性
| 名称 | 2023年浙教版七年级数学下册 第1章 平行线 单元检测卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 417.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览



文档简介
浙教版2023年七年级下册第1章《平行线》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列几组图形中,通过平移后能够重合的是( )
A. B. C. D.
2.如图,直线a、b被直线c所截,与∠1是同位角的( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如图,直线a,b被直线c所截,若a∥b,∠2=110°,则∠1的度数为( )
A.70° B.75° C.80° D.85°
4.如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,如果AD=2CE,那么BC的长是( )
A.4 B.6 C.8 D.9
5.下列说法正确的是( )
A.在同一平面内,a,b,c是直线,且a∥b,b∥c,则a∥c
B.在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c
D.在同一平面内,a,b,c是直线,且a∥b,b∥c,则a⊥c
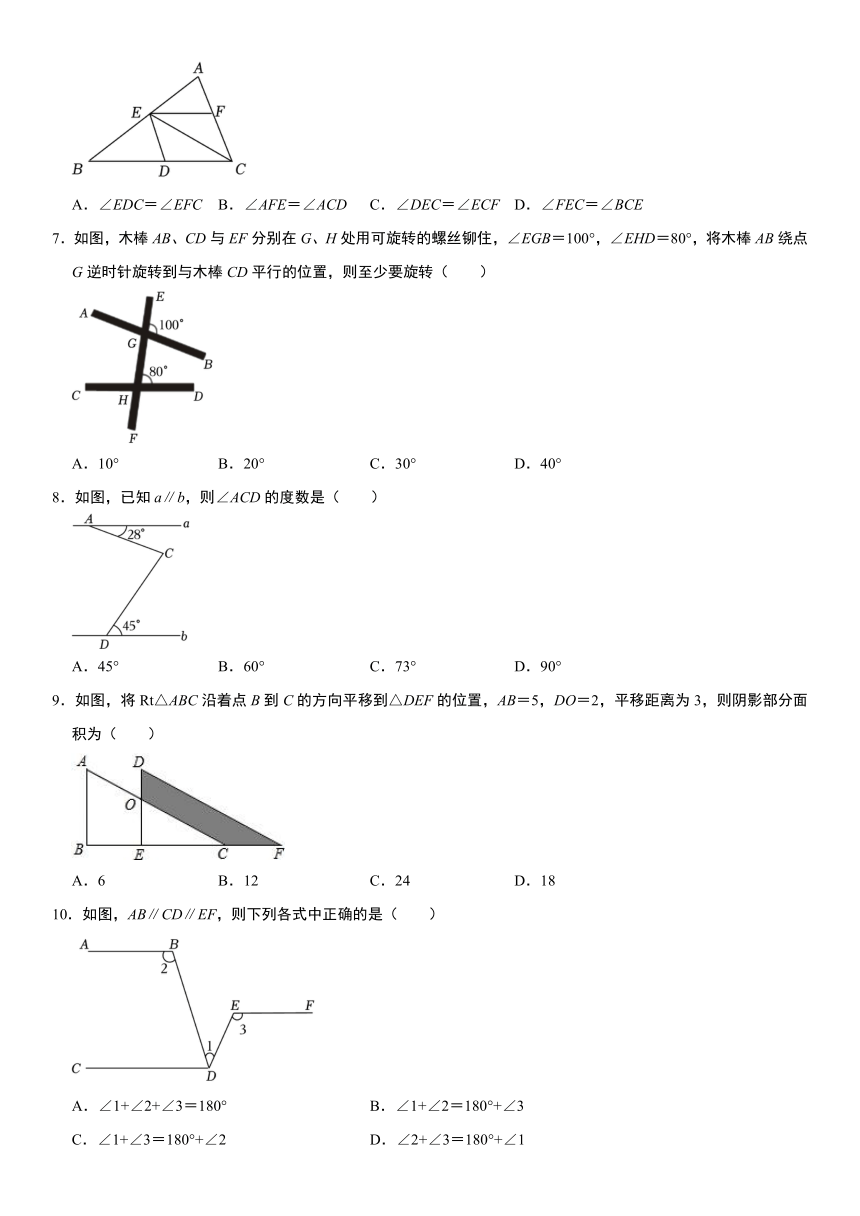
6.如图,在三角形ABC中,点E,D,F分别在AB,BC,AC上,连接ED,CE,EF,下列条件中,能推理出DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠DEC=∠ECF D.∠FEC=∠BCE
7.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10° B.20° C.30° D.40°
8.如图,已知a∥b,则∠ACD的度数是( )
A.45° B.60° C.73° D.90°
9.如图,将Rt△ABC沿着点B到C的方向平移到△DEF的位置,AB=5,DO=2,平移距离为3,则阴影部分面积为( )
A.6 B.12 C.24 D.18
10.如图,AB∥CD∥EF,则下列各式中正确的是( )
A.∠1+∠2+∠3=180° B.∠1+∠2=180°+∠3
C.∠1+∠3=180°+∠2 D.∠2+∠3=180°+∠1
二.填空题(共5小题,满分20分,每小题4分)
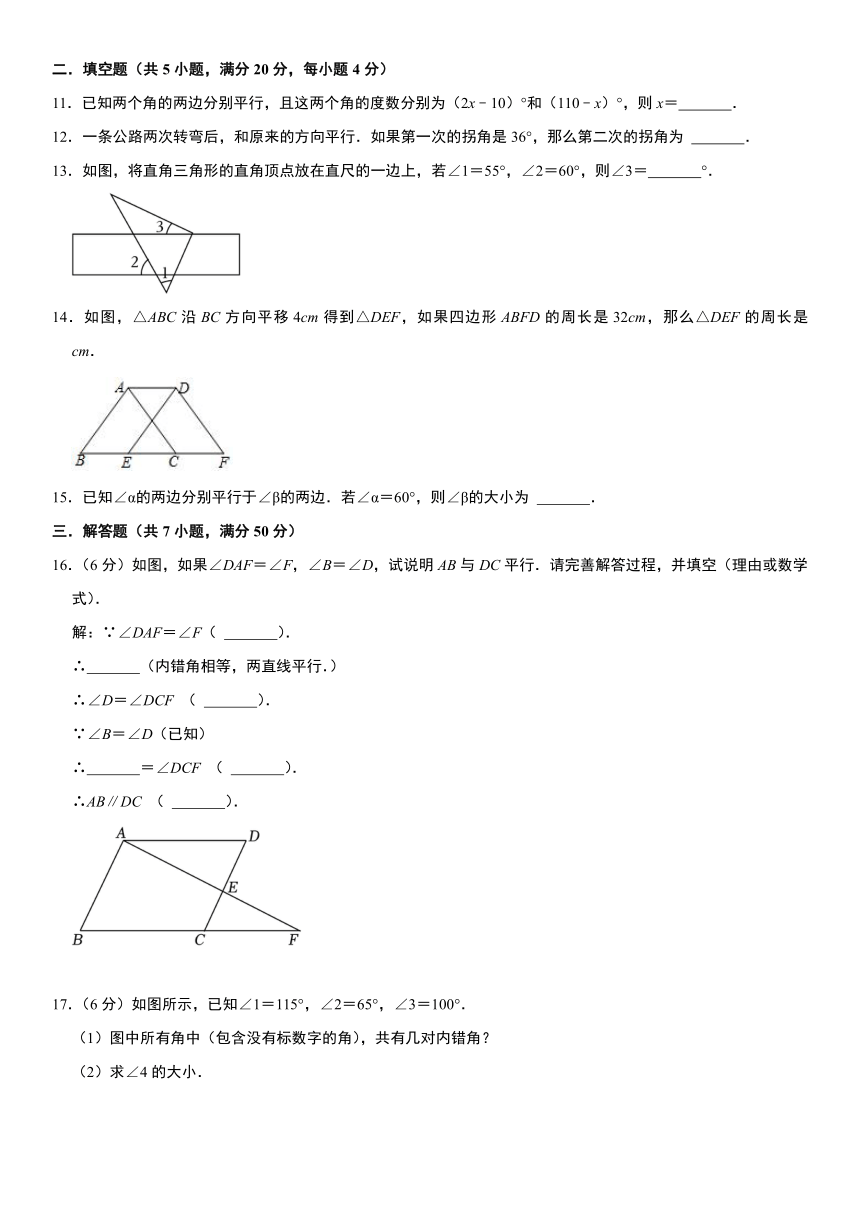
11.已知两个角的两边分别平行,且这两个角的度数分别为(2x﹣10)°和(110﹣x)°,则x= .
12.一条公路两次转弯后,和原来的方向平行.如果第一次的拐角是36°,那么第二次的拐角为 .
13.如图,将直角三角形的直角顶点放在直尺的一边上,若∠1=55°,∠2=60°,则∠3= °.
14.如图,△ABC沿BC方向平移4cm得到△DEF,如果四边形ABFD的周长是32cm,那么△DEF的周长是 cm.
15.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为 .
三.解答题(共7小题,满分50分)
16.(6分)如图,如果∠DAF=∠F,∠B=∠D,试说明AB与DC平行.请完善解答过程,并填空(理由或数学式).
解:∵∠DAF=∠F( ).
∴ (内错角相等,两直线平行.)
∴∠D=∠DCF ( ).
∵∠B=∠D(已知)
∴ =∠DCF ( ).
∴AB∥DC ( ).
17.(6分)如图所示,已知∠1=115°,∠2=65°,∠3=100°.
(1)图中所有角中(包含没有标数字的角),共有几对内错角?
(2)求∠4的大小.
18.(6分)如图,AF分别与BD、CE交于点G、H,AC分别与BD、CE交于点B、C,DF分别与BD、CE交于点D、E,∠1=55°.若∠A=∠F,∠C=∠D,求∠2的度数.
19.(6分)如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
20.(8分)(1)已知:如图1,AB∥CD,求证:∠B+∠D=∠BED;
(2)已知:如图2,AB∥CD,试探求∠B、∠D与∠E之间的数量关系,并说明理由.
拓展提升:如图3,已知AB∥DE,BF,EF分别平分∠ABC与∠CED,若∠BCE=140°,求∠BFE的度数.
21.(8分)如图,已知直线a∥b,点A、B在直线a上,点C、D在直线b上,BE平分∠ABC,DE平分∠ADC,直线BE、DE交于点E.
(1)若∠ADC=70°,∠ABC=50°,求∠BED的度数;
(2)若∠ADC=m°,∠ABC=n°,试求∠BED的度数(用含m、n的代数式表示).
22.(10分)如图,已知直线AB∥CD,∠A=∠C=100°,点E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由;
(2)求∠DBE的度数;
(3)若平行移动AD,在平行移动AD的过程中是否存在∠BEC=∠ADB?若存在,求出∠BEC的度数;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:通过平移后能够重合的是C选项中的两图形.
故选:C.
2.【解答】解:A、∠2与∠1是同位角,故本选项符合题意;
B、∠3与∠1不是同位角,故本选项不符合题意;
C、∠4与∠1是同位角,故本选项不符合题意;
D、∠5与∠1不是同位角,故本选项不符合题意;
故选:A.
3.【解答】解:如图:
∵a∥b,∠2=110°,
∴∠3=∠2=110°,
∵∠1+∠3=180°,
∴∠1=70°.
故选:A.
4.【解答】解:∵△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,
∴AD=BE=2×2=4(cm),
∵AD=2CE,
∴CE=2cm,
∴BC=BE+CE=6(cm),
故选:B.
5.【解答】解:先根据要求画出图形,图形如下图所示:
根据所画图形可知:A正确.
故选:A.
6.【解答】解:由∠EDC=∠EFC,不能判定DE∥AC,
故A不符合题意;
∵∠AFE=∠ACD,
∴EF∥BC,
故B不符合题意;
∵∠DEC=∠ECF,
∴DE∥AC,
故C符合题意;
∵∠FEC=∠BCE,
∴EF∥BC,
故D不符合题意;
故选:C.
7.【解答】解:当∠EGB=∠EHD时,AB∥CD,
∵∠EGB=100°,∠EHD=80°,
∴∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°.
故选:B.
8.【解答】解:如图,过点C作直线c∥a,则∠1=28°.
又∵a∥b,
∴c∥b,
∴∠2=45°,
∴∠ACD=28°+45°=73°.
故选:C.
9.【解答】解:∵△ABC沿B到C的方向平移到△DEF的位置,
∴S△ABC=S△DEF,
∴S阴影部分+S△OEC=S梯形ABEO+S△OEC,
∴S阴影部分=S梯形ABEO=×(5﹣2+5)×3=12.
故选:B.
10.【解答】解:∵AB∥CD∥EF,
∴∠2+∠BDC=180°,∠3=∠CDE,
又∠BDC=∠CDE﹣∠1,
∴∠2+∠3﹣∠1=180°.
故选:D.
二.填空题(共5小题,满分20分,每小题4分)
11.【解答】解:∵两个角的两边分别平行,
∴2x﹣10=110﹣x或2x﹣10+110﹣x=180,
解得:x=40或x=80.
故答案为:40或80.
12.【解答】解:如图,所示,当两次转弯后,公路的方向是相反时,
∵AB∥CD,∠D=36°,
∴∠ABD=180°﹣∠D=144°,
∴第二次的拐角为144°;
如图所示,当两次转弯后,公路的方向相同时,
∵AB∥CD,∠D=36°,
∴∠ABD=∠D=36°,
∴第二次的拐角为36°;
综上所述,第二次的拐角为36°或144°.
13.【解答】解:∵∠2和∠4为对顶角,∠2=60°,
∴∠4=∠2=60°,
∴∠5=180°﹣∠1﹣∠4=65°,
∵直尺的对边平行,
∴∠6=∠5=65°,
∵三角形为直角三角形,
∴∠3=90°﹣∠6=25°.
故答案为:25.
14.【解答】解:∵△ABC沿BC方向平移4cm得到△DEF,
∴AC=DF,AD=CF=4cm,
∵四边形ABFD的周长是32cm,
即AB+BC+CF+DF+AD=32cm,
∴AB+BC+AC+4+4=32cm,
即AB+BC+AC=24cm,
∴△ABC的周长为24cm.
∴△DEF的周长是24cm,
故答案为24.
15.【解答】解:如图1:
∵a∥b,
∴∠1=∠α,
∵c∥d,
∴∠β=∠1=∠α=60°;
如图(2),
∵a∥b,
∴∠α+∠2=180°,
∵c∥d,
∴∠2=∠β,
∴∠β+∠α=180°
∵∠α=60°,
∴∠β=120°.
综上,∠β=60°或120°.
故答案为:60°或120°.
三.解答题(共7小题,满分50分)
16.【解答】解:∵∠DAF=∠F(已知),
∴AD∥BF(内错角相等,两直线平行),
∴∠D=∠DCF(两直线平行,内错角相等),
∵∠B=∠D(已知),
∴∠B=∠DCF(等量代换),
∴AB∥DC (同位角相等,两直线平行).
17.【解答】解:如图所示:
(1)直线c和d被直线b所截,有两对内错角,
即∠2和∠6,∠5和∠7,
同理还有六对内错角,
共有8对内错角;
(2)∵∠2+∠5=180°,∠2=65°,
∴∠5=180°﹣65°=115°,
∵∠1=115°,
∴∠1=∠5,
∴a∥b,
∴∠3=∠6,
又∵∠3=100°,
∴∠6=100°,
∴∠4=∠6=100°.
18.【解答】解:∵∠A=∠F,
∴AC∥DF,
∴∠C=∠CEF,
∵∠C=∠D,
∴∠CEF=∠D,
∴BD∥CE,
∴∠1=∠AHC=55°,
∴∠2=180°﹣∠AHC=125°.
19.【解答】AB∥CD,要证明AB∥CD,即要证明∠ABC=∠BCD,即要证明∠1+∠2=∠3+∠4,由已知条件不难证明∠1+∠2=∠3+∠4.
解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3,
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4,
∵∠1+∠ABC+∠2=180°,∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD,
∴AB∥CD.
20.【解答】(1)证明:如图1,过E点作EF∥AB,
则∠1=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠B+∠D=∠1+∠2,
即∠BED=∠B+∠D.
(2)解:∠B﹣∠D=∠E,
理由:如图2,过E点作EF∥AB,
则∠BEF=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠DEF=∠CDE,
又∵∠BEF﹣∠DEF=∠BED,
∴∠B﹣∠CDE=∠BED;
(3)解:如图,过点C作CP∥AB,则∠BCP=∠ABC,∠ECP=∠CED,
∴∠ABC+∠CED=∠BCP+∠ECP=∠BCE=140°;
又∵BF,EF分别平分∠ABC,∠CED,
∴∠ABF=∠ABC,∠DEF=∠DEC;
∴∠ABF+∠DEF=(∠ABC+∠DEC)=70°,
过点F作FM∥DE,则∠BFM=∠ABF,∠MFE=∠DEF,
∴∠BFE=∠BFM+∠MFE=∠ABF+∠DEF=70°.
21.【解答】解:(1)过E作EF∥AB,
∴ABE=∠BEF,
∵∠ABC=50°,BE平分∠ABC,
∴∠ABE=∠CBE=25°,
∴∠BEF=25°,
∵a∥b,
∴AB∥CD,
∴EF∥CD,
∴∠CDE=∠DEF,
∵∠ADC=70°,DE平分∠ADC,
∴∠CDE=∠DEF=35°,
∴∠DEF=35°,
∴∠BED=∠BEF+∠DEF=60°;
(2)∵EF∥AB,
∴∠ABE=∠BEF,
∵∠ABC=n°,BE平分∠ABC,
∴∠ABE=∠CBE=n°,
∴∠BEF=,
∵a∥b,
∴AB∥CD,
∴EF∥CD,
∴∠CDE=∠DEF,
∵∠ADC=m°,DE平分∠ADC,
∴∠CDE=∠DEF=m°,
∴∠DEF=,
∴∠BED=∠BEF+∠DEF=,
即∠BED=.
22.【解答】(1)AD∥BC.
证明:∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)解:∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=∠ABF+∠CBF=∠ABC=40°;
(3)存在.
解:设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴∠BEC=∠ADB=60°.
一.选择题(共10小题,满分30分,每小题3分)
1.下列几组图形中,通过平移后能够重合的是( )
A. B. C. D.
2.如图,直线a、b被直线c所截,与∠1是同位角的( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如图,直线a,b被直线c所截,若a∥b,∠2=110°,则∠1的度数为( )
A.70° B.75° C.80° D.85°
4.如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,如果AD=2CE,那么BC的长是( )
A.4 B.6 C.8 D.9
5.下列说法正确的是( )
A.在同一平面内,a,b,c是直线,且a∥b,b∥c,则a∥c
B.在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c
D.在同一平面内,a,b,c是直线,且a∥b,b∥c,则a⊥c
6.如图,在三角形ABC中,点E,D,F分别在AB,BC,AC上,连接ED,CE,EF,下列条件中,能推理出DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠DEC=∠ECF D.∠FEC=∠BCE
7.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10° B.20° C.30° D.40°
8.如图,已知a∥b,则∠ACD的度数是( )
A.45° B.60° C.73° D.90°
9.如图,将Rt△ABC沿着点B到C的方向平移到△DEF的位置,AB=5,DO=2,平移距离为3,则阴影部分面积为( )
A.6 B.12 C.24 D.18
10.如图,AB∥CD∥EF,则下列各式中正确的是( )
A.∠1+∠2+∠3=180° B.∠1+∠2=180°+∠3
C.∠1+∠3=180°+∠2 D.∠2+∠3=180°+∠1
二.填空题(共5小题,满分20分,每小题4分)
11.已知两个角的两边分别平行,且这两个角的度数分别为(2x﹣10)°和(110﹣x)°,则x= .
12.一条公路两次转弯后,和原来的方向平行.如果第一次的拐角是36°,那么第二次的拐角为 .
13.如图,将直角三角形的直角顶点放在直尺的一边上,若∠1=55°,∠2=60°,则∠3= °.
14.如图,△ABC沿BC方向平移4cm得到△DEF,如果四边形ABFD的周长是32cm,那么△DEF的周长是 cm.
15.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为 .
三.解答题(共7小题,满分50分)
16.(6分)如图,如果∠DAF=∠F,∠B=∠D,试说明AB与DC平行.请完善解答过程,并填空(理由或数学式).
解:∵∠DAF=∠F( ).
∴ (内错角相等,两直线平行.)
∴∠D=∠DCF ( ).
∵∠B=∠D(已知)
∴ =∠DCF ( ).
∴AB∥DC ( ).
17.(6分)如图所示,已知∠1=115°,∠2=65°,∠3=100°.
(1)图中所有角中(包含没有标数字的角),共有几对内错角?
(2)求∠4的大小.
18.(6分)如图,AF分别与BD、CE交于点G、H,AC分别与BD、CE交于点B、C,DF分别与BD、CE交于点D、E,∠1=55°.若∠A=∠F,∠C=∠D,求∠2的度数.
19.(6分)如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
20.(8分)(1)已知:如图1,AB∥CD,求证:∠B+∠D=∠BED;
(2)已知:如图2,AB∥CD,试探求∠B、∠D与∠E之间的数量关系,并说明理由.
拓展提升:如图3,已知AB∥DE,BF,EF分别平分∠ABC与∠CED,若∠BCE=140°,求∠BFE的度数.
21.(8分)如图,已知直线a∥b,点A、B在直线a上,点C、D在直线b上,BE平分∠ABC,DE平分∠ADC,直线BE、DE交于点E.
(1)若∠ADC=70°,∠ABC=50°,求∠BED的度数;
(2)若∠ADC=m°,∠ABC=n°,试求∠BED的度数(用含m、n的代数式表示).
22.(10分)如图,已知直线AB∥CD,∠A=∠C=100°,点E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由;
(2)求∠DBE的度数;
(3)若平行移动AD,在平行移动AD的过程中是否存在∠BEC=∠ADB?若存在,求出∠BEC的度数;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:通过平移后能够重合的是C选项中的两图形.
故选:C.
2.【解答】解:A、∠2与∠1是同位角,故本选项符合题意;
B、∠3与∠1不是同位角,故本选项不符合题意;
C、∠4与∠1是同位角,故本选项不符合题意;
D、∠5与∠1不是同位角,故本选项不符合题意;
故选:A.
3.【解答】解:如图:
∵a∥b,∠2=110°,
∴∠3=∠2=110°,
∵∠1+∠3=180°,
∴∠1=70°.
故选:A.
4.【解答】解:∵△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,
∴AD=BE=2×2=4(cm),
∵AD=2CE,
∴CE=2cm,
∴BC=BE+CE=6(cm),
故选:B.
5.【解答】解:先根据要求画出图形,图形如下图所示:
根据所画图形可知:A正确.
故选:A.
6.【解答】解:由∠EDC=∠EFC,不能判定DE∥AC,
故A不符合题意;
∵∠AFE=∠ACD,
∴EF∥BC,
故B不符合题意;
∵∠DEC=∠ECF,
∴DE∥AC,
故C符合题意;
∵∠FEC=∠BCE,
∴EF∥BC,
故D不符合题意;
故选:C.
7.【解答】解:当∠EGB=∠EHD时,AB∥CD,
∵∠EGB=100°,∠EHD=80°,
∴∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°.
故选:B.
8.【解答】解:如图,过点C作直线c∥a,则∠1=28°.
又∵a∥b,
∴c∥b,
∴∠2=45°,
∴∠ACD=28°+45°=73°.
故选:C.
9.【解答】解:∵△ABC沿B到C的方向平移到△DEF的位置,
∴S△ABC=S△DEF,
∴S阴影部分+S△OEC=S梯形ABEO+S△OEC,
∴S阴影部分=S梯形ABEO=×(5﹣2+5)×3=12.
故选:B.
10.【解答】解:∵AB∥CD∥EF,
∴∠2+∠BDC=180°,∠3=∠CDE,
又∠BDC=∠CDE﹣∠1,
∴∠2+∠3﹣∠1=180°.
故选:D.
二.填空题(共5小题,满分20分,每小题4分)
11.【解答】解:∵两个角的两边分别平行,
∴2x﹣10=110﹣x或2x﹣10+110﹣x=180,
解得:x=40或x=80.
故答案为:40或80.
12.【解答】解:如图,所示,当两次转弯后,公路的方向是相反时,
∵AB∥CD,∠D=36°,
∴∠ABD=180°﹣∠D=144°,
∴第二次的拐角为144°;
如图所示,当两次转弯后,公路的方向相同时,
∵AB∥CD,∠D=36°,
∴∠ABD=∠D=36°,
∴第二次的拐角为36°;
综上所述,第二次的拐角为36°或144°.
13.【解答】解:∵∠2和∠4为对顶角,∠2=60°,
∴∠4=∠2=60°,
∴∠5=180°﹣∠1﹣∠4=65°,
∵直尺的对边平行,
∴∠6=∠5=65°,
∵三角形为直角三角形,
∴∠3=90°﹣∠6=25°.
故答案为:25.
14.【解答】解:∵△ABC沿BC方向平移4cm得到△DEF,
∴AC=DF,AD=CF=4cm,
∵四边形ABFD的周长是32cm,
即AB+BC+CF+DF+AD=32cm,
∴AB+BC+AC+4+4=32cm,
即AB+BC+AC=24cm,
∴△ABC的周长为24cm.
∴△DEF的周长是24cm,
故答案为24.
15.【解答】解:如图1:
∵a∥b,
∴∠1=∠α,
∵c∥d,
∴∠β=∠1=∠α=60°;
如图(2),
∵a∥b,
∴∠α+∠2=180°,
∵c∥d,
∴∠2=∠β,
∴∠β+∠α=180°
∵∠α=60°,
∴∠β=120°.
综上,∠β=60°或120°.
故答案为:60°或120°.
三.解答题(共7小题,满分50分)
16.【解答】解:∵∠DAF=∠F(已知),
∴AD∥BF(内错角相等,两直线平行),
∴∠D=∠DCF(两直线平行,内错角相等),
∵∠B=∠D(已知),
∴∠B=∠DCF(等量代换),
∴AB∥DC (同位角相等,两直线平行).
17.【解答】解:如图所示:
(1)直线c和d被直线b所截,有两对内错角,
即∠2和∠6,∠5和∠7,
同理还有六对内错角,
共有8对内错角;
(2)∵∠2+∠5=180°,∠2=65°,
∴∠5=180°﹣65°=115°,
∵∠1=115°,
∴∠1=∠5,
∴a∥b,
∴∠3=∠6,
又∵∠3=100°,
∴∠6=100°,
∴∠4=∠6=100°.
18.【解答】解:∵∠A=∠F,
∴AC∥DF,
∴∠C=∠CEF,
∵∠C=∠D,
∴∠CEF=∠D,
∴BD∥CE,
∴∠1=∠AHC=55°,
∴∠2=180°﹣∠AHC=125°.
19.【解答】AB∥CD,要证明AB∥CD,即要证明∠ABC=∠BCD,即要证明∠1+∠2=∠3+∠4,由已知条件不难证明∠1+∠2=∠3+∠4.
解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3,
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4,
∵∠1+∠ABC+∠2=180°,∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD,
∴AB∥CD.
20.【解答】(1)证明:如图1,过E点作EF∥AB,
则∠1=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠B+∠D=∠1+∠2,
即∠BED=∠B+∠D.
(2)解:∠B﹣∠D=∠E,
理由:如图2,过E点作EF∥AB,
则∠BEF=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠DEF=∠CDE,
又∵∠BEF﹣∠DEF=∠BED,
∴∠B﹣∠CDE=∠BED;
(3)解:如图,过点C作CP∥AB,则∠BCP=∠ABC,∠ECP=∠CED,
∴∠ABC+∠CED=∠BCP+∠ECP=∠BCE=140°;
又∵BF,EF分别平分∠ABC,∠CED,
∴∠ABF=∠ABC,∠DEF=∠DEC;
∴∠ABF+∠DEF=(∠ABC+∠DEC)=70°,
过点F作FM∥DE,则∠BFM=∠ABF,∠MFE=∠DEF,
∴∠BFE=∠BFM+∠MFE=∠ABF+∠DEF=70°.
21.【解答】解:(1)过E作EF∥AB,
∴ABE=∠BEF,
∵∠ABC=50°,BE平分∠ABC,
∴∠ABE=∠CBE=25°,
∴∠BEF=25°,
∵a∥b,
∴AB∥CD,
∴EF∥CD,
∴∠CDE=∠DEF,
∵∠ADC=70°,DE平分∠ADC,
∴∠CDE=∠DEF=35°,
∴∠DEF=35°,
∴∠BED=∠BEF+∠DEF=60°;
(2)∵EF∥AB,
∴∠ABE=∠BEF,
∵∠ABC=n°,BE平分∠ABC,
∴∠ABE=∠CBE=n°,
∴∠BEF=,
∵a∥b,
∴AB∥CD,
∴EF∥CD,
∴∠CDE=∠DEF,
∵∠ADC=m°,DE平分∠ADC,
∴∠CDE=∠DEF=m°,
∴∠DEF=,
∴∠BED=∠BEF+∠DEF=,
即∠BED=.
22.【解答】(1)AD∥BC.
证明:∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)解:∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=∠ABF+∠CBF=∠ABC=40°;
(3)存在.
解:设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴∠BEC=∠ADB=60°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
