七下数学第3章3.2单项式的乘法

(共15张PPT)
5.2 单项式的乘法
合作学习
一幅电脑画的尺寸如图所示
m
m
a
b
请用两种不同的方法表示画面的面积
这两种不同的方法表示的面积应该相等，你能说明理由吗？
通过上面的讨论， 你能总结出单项式 与多项式相乘的规 律吗？
一位旅行者用步长测量天安门广场的面积：他从南走到北，记下所走的步数为1100步；再从东走到西，记下所走的步数为625步，然后根据自己的步长来估算广场的面积。
（1）如果该旅行者的步长用a米表示，你能用含a的代数式表示广场的面积吗？
（2）假设这位旅行者的步长为0.8米，那么广场的面积大约是多少？
（3）通过解决上述问题，你认为两个单项式相乘应怎样运算？运算的依据是什么？
1100a×625a
1100×0.8×625×0.8
一:合并下列各项
×
×
=3 ×a ×b × 4×a ×c
=(3 ×4) ×(a × a) ×b ×c
=12a2bc
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式
例1:计算
解:原式
解:原式
解:原式
解:原式
练习:
P68 课内练习1
计算:
⑴ -3a (2b) ⑵ 1.5x2 (-2x3)
⑶ (-2/3st2) (-1/2s2t) ⑷ (-2a)3 2ab2
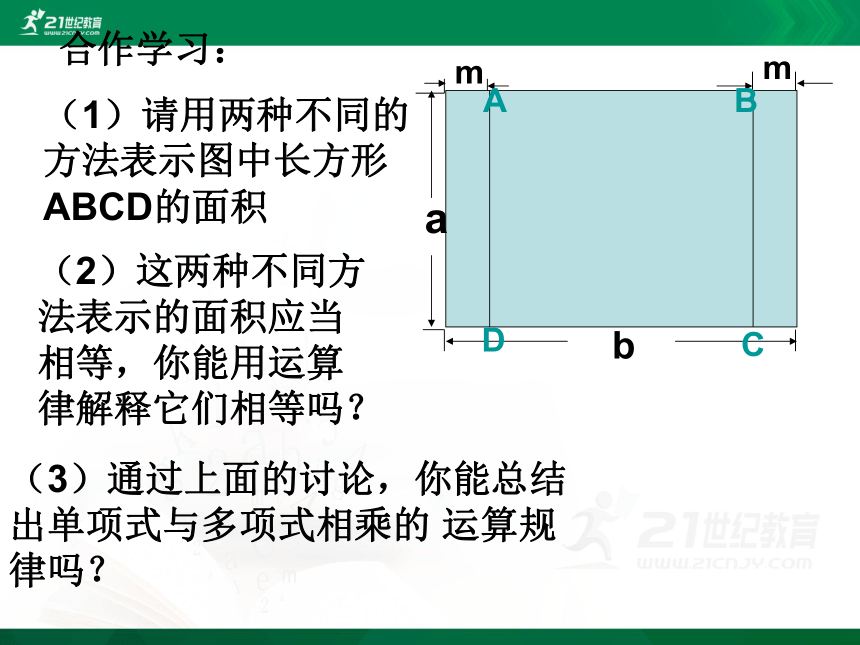
合作学习：
（1）请用两种不同的
方法表示图中长方形
ABCD的面积
a
m
b
m
A
B
C
D
（2）这两种不同方法表示的面积应当相等，你能用运算律解释它们相等吗？
（3）通过上面的讨论，你能总结出单项式与多项式相乘的 运算规律吗？
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加
单项式与多项式相乘的法则：
例2 计算：
(1)(-4x)·(2x2+3x-1)；
解： (-4x)·(2x2+3x-1)
＝(-4x)·(2x2)+(-4x)·3x+(-4x)·(-1)
＝-8x3-12x2+4x；
注意(-1)这项不要漏乘，也不要当成是1；
例3:计算
解:原式=
解:原式=
几点注意：
1.单项式乘多项式的结果仍是多项式，积的项数与原多项式的项数相同。
2.单项式分别与多项式的每一项相乘时，要注意积的各项符号的确定：同号相乘得正，异号相乘得负
3.不要出现漏乘现象，运算要有顺序。
形成性测试
一.判断
×
×
√
1.m(a+b+c+d)=ma+b+c+d( )
( )
3.(-2x) （ax+b-3)=-2ax2-2bx-6x( )
×
4.一个单项式乘以一个多项式，所得的结果
仍是一个多项式( )
1.单项式与多项式相乘，就是用单项式去乘
多项式的________,再把所得的积________
二.填空
2.4（a-b+1)=___________________
每一项
相加
4a-4b+4
3.3x（2x-y2)=___________________
6x2-3xy2
4.-3x（2x-5y+6z)=___________________
-6x2+15xy-18xz
5.(-2a2)2（-a-2b+c)=___________________
-4a5-8a4b+4a4c
动脑筋：
分别计算下列图形中绿色或蓝色部分的面积
a/2
a
t
t
b
1
2
总结
1: 单项式与单项式相乘,把它们的 分
别相乘,其余 不变,作为积的因式
2: 单项式与多项式相乘,就是用单项式去乘,
再把所得的积相加
系数、同底数幂
字母连同它的指数
多项式的每一项