浙教版数学七年级下册第1章《平行线》单元练习卷(2份试卷 无答案)
文档属性
| 名称 | 浙教版数学七年级下册第1章《平行线》单元练习卷(2份试卷 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 704.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 09:58:16 | ||
图片预览


文档简介
七年级下册数学《学能测评》单元试卷(一)
第1章《平行线》单元练习卷
班级__________姓名__________学号__________成绩__________
一、选择题(每题3分,共30 分)
1.在下列图形中,∠1与 ∠2 是同位角的是( )
A. B. C. D.
2.下列图形不能由“基本图案”通过平移得到的是( )
A. B.
D.
3.如图,将△ABC沿水平方向向右平移到△DEF 的位置,已知点 A 和 D 之间的距离为 1,CE=2,则 BF 的长为( )
A. 2 B. 3 C. 4 D. 5
4.如图,能判定DE∥AC 的条件是( )
A.∠3=∠C B.∠1=∠3 C.∠2= ∠4 D.∠1+∠2 =180°
(第3题图) (第4题图) (第6题图)
5.如图所示,将一张长方形纸对折三次,所产生的折痕与折痕间的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
6.如图,把一块含45°角的直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2为( )
A. 33° B. 57° C. 67° D. 60°
7.下列条件中,能说明AD//BC的条件有( )个
①∠1=∠4 ②∠2=∠3 ③∠A+∠ABC=180°④∠A+∠ADC=180°
A. 1 B. 2 C. 3 D. 4
8.一副三角板如图放置,斜边互相平行,且每个三角板的直角顶点都在另一个三角板的斜边上,在图中所标记的角中,与∠1相等的角是( )
A. ∠2 B. ∠3 C. ∠4 D. ∠5
9.如图,将△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A. 42 B. 48 C. 84 D. 96
(第7题图) (第8题图) (第9题图)
10.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
(第10题图) (第12题图) (第13题图)
填空题(每题4 分,共32分)
在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③钟摆的摆动,④随风摆动的旗帜,其中属于平移现象的有 (只填序号).
12.如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为 .
13.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为 度.
14.如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有 .(填写正确的序号)
(第14题图) (第15题图) (第16题图)
15.如图,某酒店重新装修后,准备在大厅主楼梯上铺设红色地毯.已知这种地毯每平方米售价160元,主楼梯道宽2.5m,其侧面如图所示,则购买地毯至少需要 元.
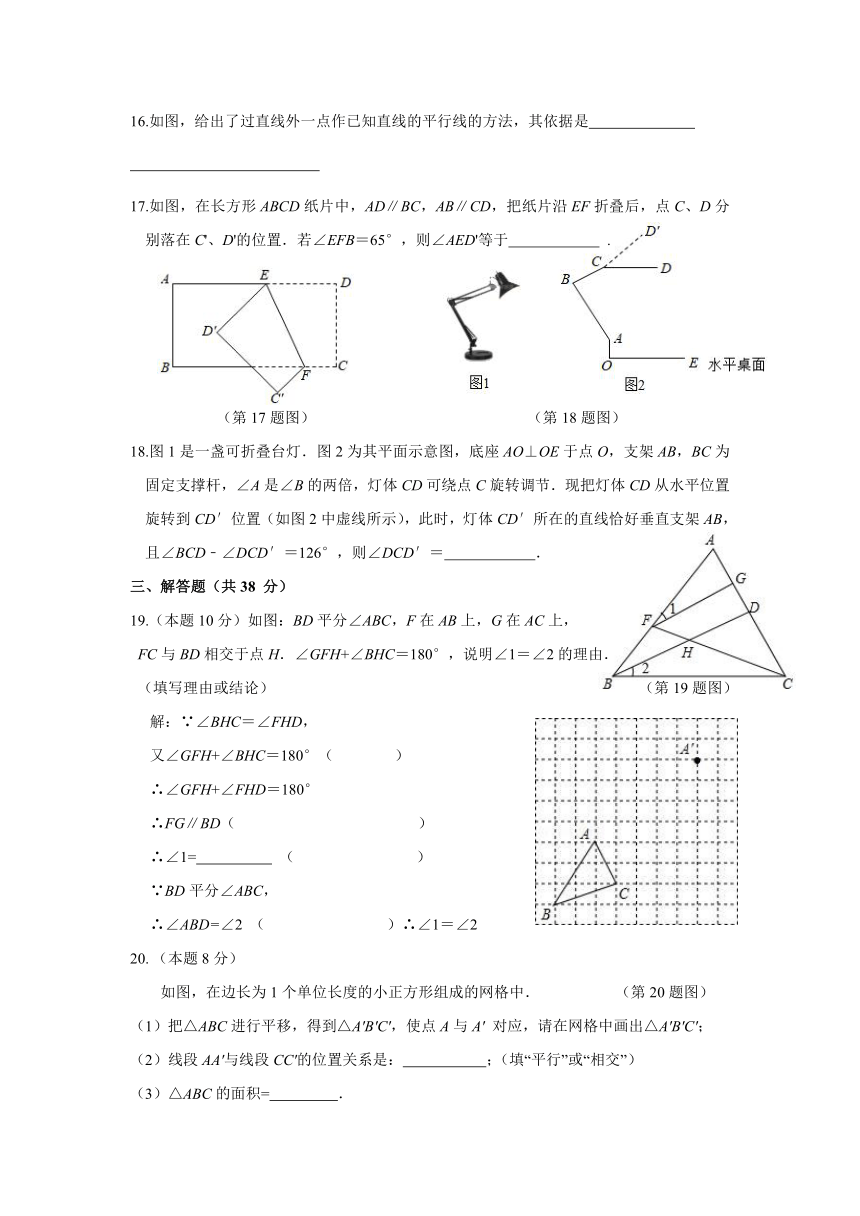
16.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
17.如图,在长方形ABCD纸片中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C、D分别落在C'、D'的位置.若∠EFB=65°,则∠AED'等于 .
(第17题图) (第18题图)
18.图1是一盏可折叠台灯.图2为其平面示意图,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠A是∠B的两倍,灯体CD可绕点C旋转调节.现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示),此时,灯体CD′所在的直线恰好垂直支架AB,且∠BCD﹣∠DCD′=126°,则∠DCD′= .
解答题(共38 分)
19.(本题10分)如图:BD平分∠ABC,F在AB上,G在AC上,
FC与BD相交于点H.∠GFH+∠BHC=180°,说明∠1=∠2的理由.
(填写理由或结论) (第19题图)
解:∵∠BHC=∠FHD,
又∠GFH+∠BHC=180°( )
∴∠GFH+∠FHD=180°
∴FG∥BD( )
∴∠1= ( )
∵BD平分∠ABC,
∴∠ABD=∠2 ( )∴∠1=∠2
(本题8分)
如图,在边长为1个单位长度的小正方形组成的网格中. (第20题图)
(1)把△ABC进行平移,得到△A′B′C′,使点A与A′ 对应,请在网格中画出△A′B′C′;
线段AA′与线段CC′的位置关系是: ;(填“平行”或“相交”)
(3)△ABC的面积= .
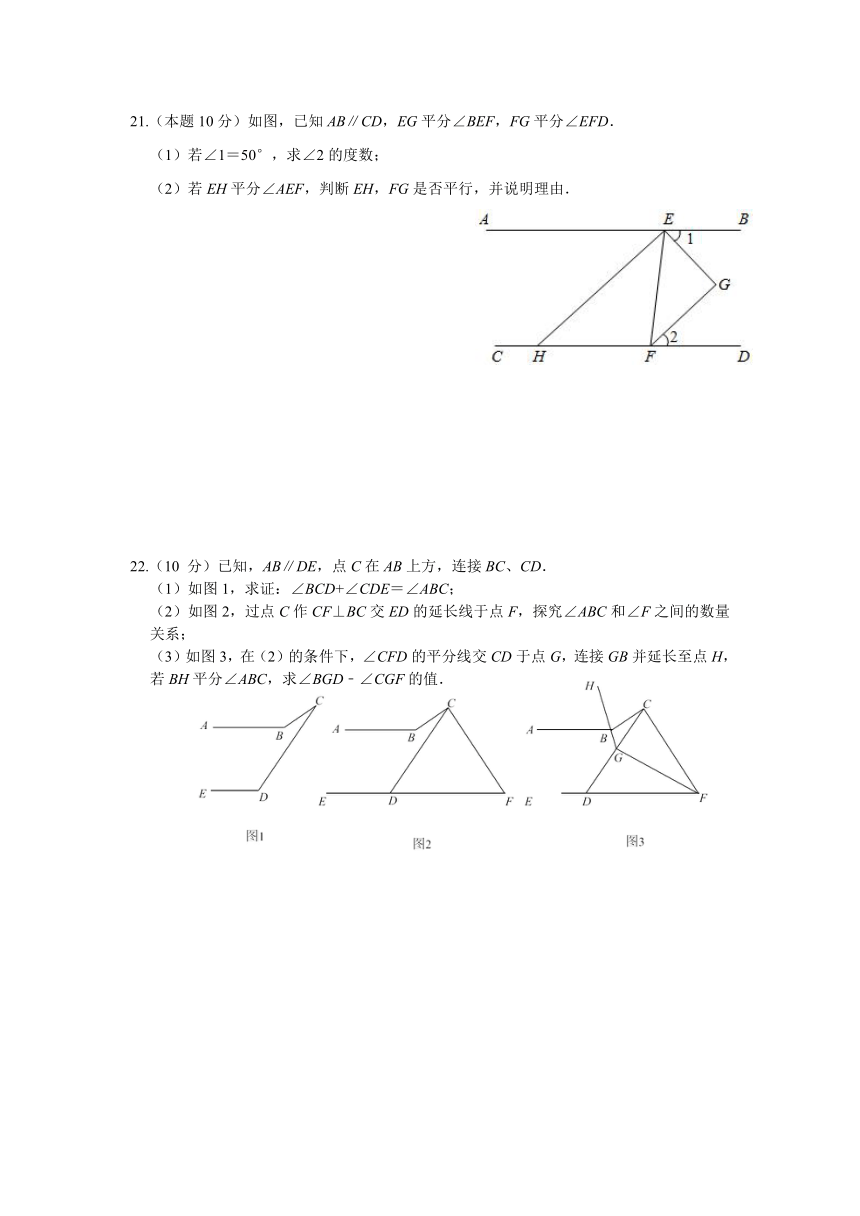
21.(本题10分)如图,已知AB∥CD,EG平分∠BEF,FG平分∠EFD.
(1)若∠1=50°,求∠2的度数;
(2)若EH平分∠AEF,判断EH,FG是否平行,并说明理由.
22.(10 分)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
七年级下册数学《学能测评》单元试卷(二)
第1章《平行线》单元测试卷
班级__________姓名__________学号__________成绩__________
选择题(每题3分,共30 分)
1.在同一平面内,两条直线的位置关系可能是( )
A.相交或平行 B.相交或垂直 C.平行或垂直 D.不能确定
2.如图,射线AB,AC被射线DE所截,图中的∠1与∠2是( )
A.内错角 B.对顶角 C.同位角 D.同旁内角
3.下列结论错误的是( )
A.平行于同一直线的两直线也互相平行 B.同旁内角互补,两直线平行
C.两直线平行,内错角相等 D.不相交的两条直线叫做平行线
4.如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是( )
A.∠3=∠1+∠2 B.∠2+∠3﹣∠1=90°
C.∠1﹣∠2+∠3=180° D.∠2+∠3﹣∠1=180°
(第2题图) (第4题图) (第5题图)
5.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
6.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )
A.30° B.60° C.30°或60° D.60°或120°
7.如图,平行线AB,CD被直线AE所截,∠1=110°,则下列结论正确的是( )
A.∠2=110° B.∠3=70° C.∠4=70° D.∠5=70°
(第7题图) (第8题图) (第9题图)
在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了所有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转,向右平移 B.逆时针旋转,向右平移
C.顺时针旋转,向下平移 D.逆时针旋转,向下平移
9.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( )
A.26° B.52° C.54° D.77°
10.已知:如图7,D是射线AB上一动点,连结CD,过点D作DE∥BC交直线AC于点E.若∠ABC=84°,∠CDE=20°,则∠ADC的度数为( )
A.104° B.76° C.104°或64° D.104°或76°
(第10题图) (第11题图) (第12题图)
二、填空题(每题4 分,共32分)
11.如图,梯子的各条横档互相平行,若∠1=105°,则∠2= °.
12.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'= .
13.如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,则BE与AC的位置关是 .
(第13题图) (第14题图) (第15题图)
14.如图,按虚线剪去长方形纸片相邻的两个角,并使∠1=120°,∠ABC=90°,则∠2的度数为 .
15.小同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP= °.
16.如图,要判定AB∥CD,需添加的条件是 .
(第16题图) (第17题图) (第18题图)
17.如图,a∥b,点B在直线b上,且AB⊥BC,∠1=35°,那么∠2=______ .
18.如图,AB∥CD,AD与BC相交于点F,BE平分∠ABC,DE平分∠ADC,∠AFB=96°,则∠BED的度数为 度.
三、解答题(38分)
19.(本题10分)如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵CD⊥DA,DA⊥AB(___________)
∴∠CDA=90°,∠DAB=90°( )
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴( ),∴DF∥AE( ).
20.(本题8分)如图:已知,∠A=120°,∠ABC=60°,BD⊥DC于点D,EF⊥DC于点F,
(1)说明AD∥BC的理由;
(2)若∠1=40°,求∠2的度数.
21.(本题10分)如图,已知AC∥FE,∠1+∠2=180°.
(1)说明∠FAB=∠BDC的理由;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
22.(本题10分)如图,BD是∠ABC的角平分线,∠ABE+∠BCF=180°.
(1)若∠ABC=80°,求∠BCF的值;
(2)说明DE∥CF的理由;
(3)若CB是∠ACF的角平分线,∠ADB=k∠ABD,求k的值.
第1章《平行线》单元练习卷
班级__________姓名__________学号__________成绩__________
一、选择题(每题3分,共30 分)
1.在下列图形中,∠1与 ∠2 是同位角的是( )
A. B. C. D.
2.下列图形不能由“基本图案”通过平移得到的是( )
A. B.
D.
3.如图,将△ABC沿水平方向向右平移到△DEF 的位置,已知点 A 和 D 之间的距离为 1,CE=2,则 BF 的长为( )
A. 2 B. 3 C. 4 D. 5
4.如图,能判定DE∥AC 的条件是( )
A.∠3=∠C B.∠1=∠3 C.∠2= ∠4 D.∠1+∠2 =180°
(第3题图) (第4题图) (第6题图)
5.如图所示,将一张长方形纸对折三次,所产生的折痕与折痕间的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
6.如图,把一块含45°角的直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2为( )
A. 33° B. 57° C. 67° D. 60°
7.下列条件中,能说明AD//BC的条件有( )个
①∠1=∠4 ②∠2=∠3 ③∠A+∠ABC=180°④∠A+∠ADC=180°
A. 1 B. 2 C. 3 D. 4
8.一副三角板如图放置,斜边互相平行,且每个三角板的直角顶点都在另一个三角板的斜边上,在图中所标记的角中,与∠1相等的角是( )
A. ∠2 B. ∠3 C. ∠4 D. ∠5
9.如图,将△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A. 42 B. 48 C. 84 D. 96
(第7题图) (第8题图) (第9题图)
10.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
(第10题图) (第12题图) (第13题图)
填空题(每题4 分,共32分)
在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③钟摆的摆动,④随风摆动的旗帜,其中属于平移现象的有 (只填序号).
12.如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为 .
13.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为 度.
14.如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有 .(填写正确的序号)
(第14题图) (第15题图) (第16题图)
15.如图,某酒店重新装修后,准备在大厅主楼梯上铺设红色地毯.已知这种地毯每平方米售价160元,主楼梯道宽2.5m,其侧面如图所示,则购买地毯至少需要 元.
16.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
17.如图,在长方形ABCD纸片中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C、D分别落在C'、D'的位置.若∠EFB=65°,则∠AED'等于 .
(第17题图) (第18题图)
18.图1是一盏可折叠台灯.图2为其平面示意图,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠A是∠B的两倍,灯体CD可绕点C旋转调节.现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示),此时,灯体CD′所在的直线恰好垂直支架AB,且∠BCD﹣∠DCD′=126°,则∠DCD′= .
解答题(共38 分)
19.(本题10分)如图:BD平分∠ABC,F在AB上,G在AC上,
FC与BD相交于点H.∠GFH+∠BHC=180°,说明∠1=∠2的理由.
(填写理由或结论) (第19题图)
解:∵∠BHC=∠FHD,
又∠GFH+∠BHC=180°( )
∴∠GFH+∠FHD=180°
∴FG∥BD( )
∴∠1= ( )
∵BD平分∠ABC,
∴∠ABD=∠2 ( )∴∠1=∠2
(本题8分)
如图,在边长为1个单位长度的小正方形组成的网格中. (第20题图)
(1)把△ABC进行平移,得到△A′B′C′,使点A与A′ 对应,请在网格中画出△A′B′C′;
线段AA′与线段CC′的位置关系是: ;(填“平行”或“相交”)
(3)△ABC的面积= .
21.(本题10分)如图,已知AB∥CD,EG平分∠BEF,FG平分∠EFD.
(1)若∠1=50°,求∠2的度数;
(2)若EH平分∠AEF,判断EH,FG是否平行,并说明理由.
22.(10 分)已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
七年级下册数学《学能测评》单元试卷(二)
第1章《平行线》单元测试卷
班级__________姓名__________学号__________成绩__________
选择题(每题3分,共30 分)
1.在同一平面内,两条直线的位置关系可能是( )
A.相交或平行 B.相交或垂直 C.平行或垂直 D.不能确定
2.如图,射线AB,AC被射线DE所截,图中的∠1与∠2是( )
A.内错角 B.对顶角 C.同位角 D.同旁内角
3.下列结论错误的是( )
A.平行于同一直线的两直线也互相平行 B.同旁内角互补,两直线平行
C.两直线平行,内错角相等 D.不相交的两条直线叫做平行线
4.如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是( )
A.∠3=∠1+∠2 B.∠2+∠3﹣∠1=90°
C.∠1﹣∠2+∠3=180° D.∠2+∠3﹣∠1=180°
(第2题图) (第4题图) (第5题图)
5.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
6.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )
A.30° B.60° C.30°或60° D.60°或120°
7.如图,平行线AB,CD被直线AE所截,∠1=110°,则下列结论正确的是( )
A.∠2=110° B.∠3=70° C.∠4=70° D.∠5=70°
(第7题图) (第8题图) (第9题图)
在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了所有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转,向右平移 B.逆时针旋转,向右平移
C.顺时针旋转,向下平移 D.逆时针旋转,向下平移
9.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( )
A.26° B.52° C.54° D.77°
10.已知:如图7,D是射线AB上一动点,连结CD,过点D作DE∥BC交直线AC于点E.若∠ABC=84°,∠CDE=20°,则∠ADC的度数为( )
A.104° B.76° C.104°或64° D.104°或76°
(第10题图) (第11题图) (第12题图)
二、填空题(每题4 分,共32分)
11.如图,梯子的各条横档互相平行,若∠1=105°,则∠2= °.
12.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'= .
13.如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,则BE与AC的位置关是 .
(第13题图) (第14题图) (第15题图)
14.如图,按虚线剪去长方形纸片相邻的两个角,并使∠1=120°,∠ABC=90°,则∠2的度数为 .
15.小同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP= °.
16.如图,要判定AB∥CD,需添加的条件是 .
(第16题图) (第17题图) (第18题图)
17.如图,a∥b,点B在直线b上,且AB⊥BC,∠1=35°,那么∠2=______ .
18.如图,AB∥CD,AD与BC相交于点F,BE平分∠ABC,DE平分∠ADC,∠AFB=96°,则∠BED的度数为 度.
三、解答题(38分)
19.(本题10分)如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵CD⊥DA,DA⊥AB(___________)
∴∠CDA=90°,∠DAB=90°( )
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴( ),∴DF∥AE( ).
20.(本题8分)如图:已知,∠A=120°,∠ABC=60°,BD⊥DC于点D,EF⊥DC于点F,
(1)说明AD∥BC的理由;
(2)若∠1=40°,求∠2的度数.
21.(本题10分)如图,已知AC∥FE,∠1+∠2=180°.
(1)说明∠FAB=∠BDC的理由;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
22.(本题10分)如图,BD是∠ABC的角平分线,∠ABE+∠BCF=180°.
(1)若∠ABC=80°,求∠BCF的值;
(2)说明DE∥CF的理由;
(3)若CB是∠ACF的角平分线,∠ADB=k∠ABD,求k的值.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
