第1章 平行线 单元检测卷（含答案）

中小学教育资源及组卷应用平台
浙教版2023年七年级下册 第1章 平行线 单元检测卷
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）在同一平面内，两直线的位置关系必是（　　）
A．相交 B．平行 C．相交或平行 D．垂直
2．（3分）若将如图平移，则得到的图形是（　　）
A． B．
C． D．
3．（3分）如图，直线a，b被c所截，则∠1与∠2是（　　）
A．邻补角 B．同位角 C．内错角 D．同旁内角
4．（3分）如图，直线a，b被直线c所截，若a∥b，∠2＝110°，则∠1的度数为（　　）
A．70° B．75° C．80° D．85°
5．（3分）下列说法正确的是（　　）
A．a、b、c是直线，若a⊥b，b∥c，则a∥c
B．a、b、c是直线，若a⊥b，b⊥c，则a⊥c
C．a、b、c是直线，若a∥b，b⊥c，则a∥c
D．a、b、c是直线，若a∥b，b∥c，则a∥c
6．（3分）如图，下列推理中，正确的是（　　）
A．如果∠2＝∠4，那么AD∥BC
B．如果∠1＝∠3，那么AD∥BC
C．如果∠4+∠D＝180°，那么AD∥BC
D．如果∠4+∠B＝180°，那么AB∥DC
7．（3分）如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠2＝40°，则∠1＝（　　）
A．60° B．50° C．40° D．30°
8．（3分）如图，三角形ABC的周长是16cm，将三角形ABC向右平移3cm得到三角形DEF，则四边形ABFD的周长是（　　）
A．16cm B．18cm C．20cm D．22cm
9．（3分）如图，把一张长方形的纸按图那样折叠后，B，C两点落在B1，C1处，若∠AEB1＝70°，则∠BEF＝（　　）
A．70° B．60° C．65° D．55°
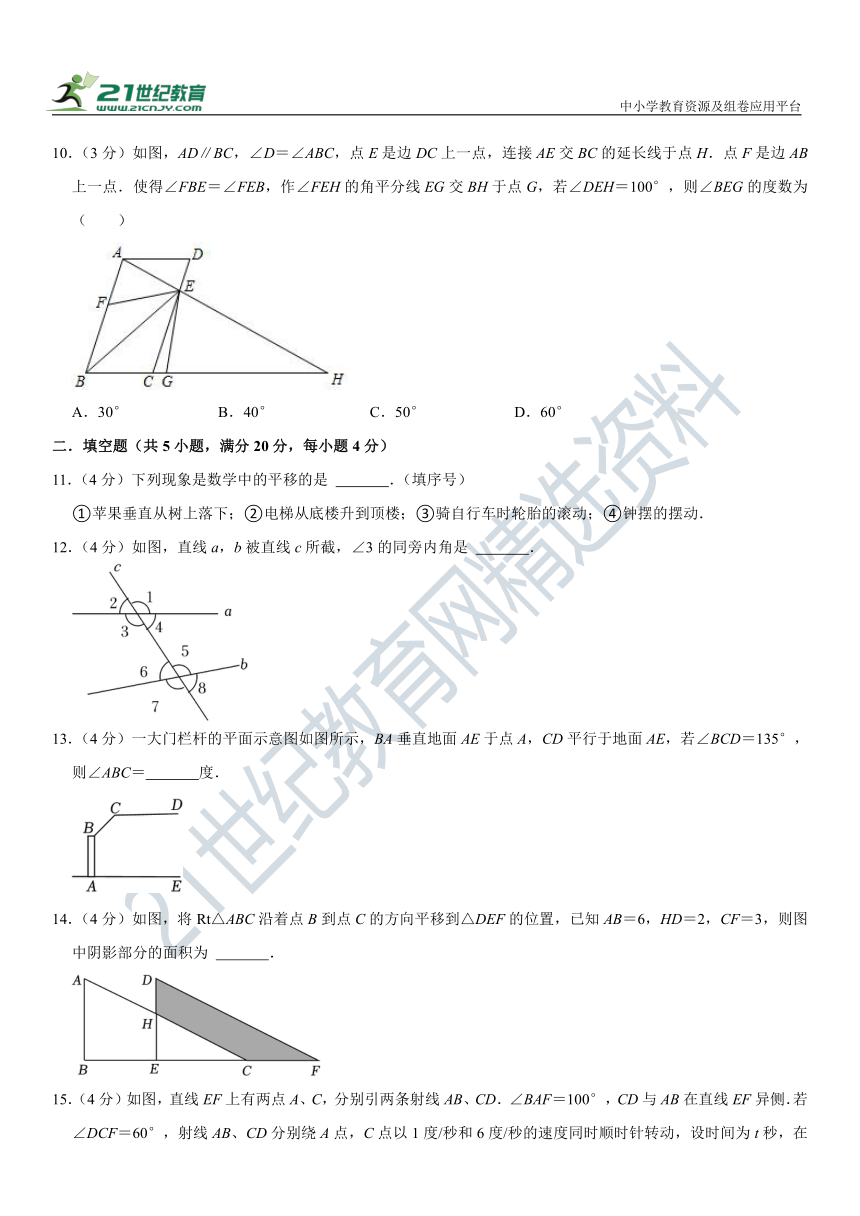
10．（3分）如图，AD∥BC，∠D＝∠ABC，点E是边DC上一点，连接AE交BC的延长线于点H．点F是边AB上一点．使得∠FBE＝∠FEB，作∠FEH的角平分线EG交BH于点G，若∠DEH＝100°，则∠BEG的度数为（　　）
A．30° B．40° C．50° D．60°
二．填空题（共5小题，满分20分，每小题4分）
11．（4分）下列现象是数学中的平移的是 　 　．（填序号）
①苹果垂直从树上落下；②电梯从底楼升到顶楼；③骑自行车时轮胎的滚动；④钟摆的摆动．
12．（4分）如图，直线a，b被直线c所截，∠3的同旁内角是 　 　．
13．（4分）一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD＝135°，则∠ABC＝　 　度．
14．（4分）如图，将Rt△ABC沿着点B到点C的方向平移到△DEF的位置，已知AB＝6，HD＝2，CF＝3，则图中阴影部分的面积为 　 　．
15．（4分）如图，直线EF上有两点A、C，分别引两条射线AB、CD．∠BAF＝100°，CD与AB在直线EF异侧．若∠DCF＝60°，射线AB、CD分别绕A点，C点以1度/秒和6度/秒的速度同时顺时针转动，设时间为t秒，在射线CD转动一周的时间内，当时间t的值为 　 　时，CD与AB平行．
三．解答题（共7小题，满分50分）
16．（6分）如图，指出图中直线AC，BC被直线AB所截的同位角、内错角、同旁内角．
17．（6分）如图，已知∠BAD＝∠DCB，∠1＝∠3，求证：AD∥BC．
证明：∵∠BAD＝∠DCB，∠1＝∠3（ 　 　），
∴∠BAD﹣　 　＝∠DCB﹣　 　（等式的性质），
即 　 　＝　 　．
∴AD∥BC （ 　 　）．
18．（6分）已知：如图，AE与BD相交于点F，∠B＝∠C，∠1＝∠2．求证：AB∥CE．
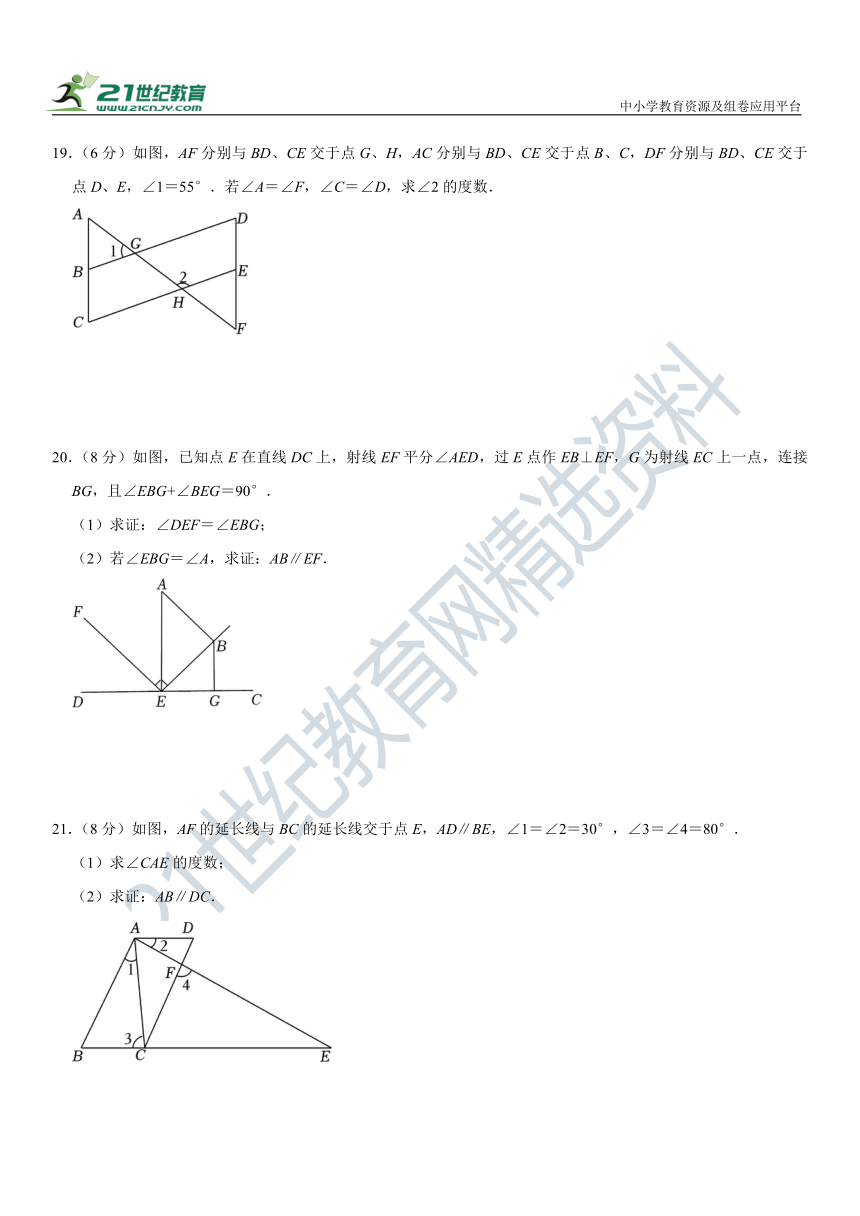
19．（6分）如图，AF分别与BD、CE交于点G、H，AC分别与BD、CE交于点B、C，DF分别与BD、CE交于点D、E，∠1＝55°．若∠A＝∠F，∠C＝∠D，求∠2的度数．
20．（8分）如图，已知点E在直线DC上，射线EF平分∠AED，过E点作EB⊥EF，G为射线EC上一点，连接BG，且∠EBG+∠BEG＝90°．
（1）求证：∠DEF＝∠EBG；
（2）若∠EBG＝∠A，求证：AB∥EF．
21．（8分）如图，AF的延长线与BC的延长线交于点E，AD∥BE，∠1＝∠2＝30°，∠3＝∠4＝80°．
（1）求∠CAE的度数；
（2）求证：AB∥DC．
22．（10分）如图1，已知AC∥BD，点P是直线AC，BD间的一点，连接AB，AP，BP，过点P作直线MN∥AC．
（1）MN与BD的位置关系是什么，请说明理由；
（2）试说明∠APB＝∠PBD+∠PAC；
（3）如图2，当点P在直线AC上方时，（2）中的三个角的数量关系是否仍然成立？如果成立，试说明理由；如果不成立，试探索它们存在的关系，并说明理由．
参考答案
一．选择题（共10小题，满分30分，每小题3分）
1．【解答】解：在同一个平面内，两条直线只有两种位置关系，即平行或相交．
故选：C．
2．【解答】解：将图中所示的图案平移后得到的图案是：
，
故选：C．
3．【解答】解：∠1与∠2是内错角．
故选：C．
4．【解答】解：如图：
∵a∥b，∠2＝110°，
∴∠3＝∠2＝110°，
∵∠1+∠3＝180°，
∴∠1＝70°．
故选：A．
5．【解答】解：A、∵a⊥b，b∥c，
∴a⊥c，故本选项错误；
B、在同一平面内，当a⊥b，b⊥c时，a∥c，故本选项错误；
C、当a∥b，b⊥c时，a⊥c，故本选项错误；
D、当a∥b，b∥c时，a∥c，故选项正确；
故选：D．
6．【解答】解：A、由内错角相等，两直线平行可知如果∠2＝∠4，那么AB∥CD，不能得到AD∥BC，故此选项不符合题意；
B、由内错角相等，两直线平行可知如果∠1＝∠3，那么AD∥BC，故此选项符合题意；
C、由同旁内角互补，两直线平行可知，如果∠3+∠4+∠D＝180°，那么AD∥BC，，故此选项不符合题意；
D、由同旁内角互补，两直线平行可知，如果∠3+∠4+∠B＝180°，那么AB∥DC，故此选项不符合题意；
故选：B．
7．【解答】解：如图，
∵∠2＝40°，
∴∠3＝90°﹣∠2＝50°，
∴∠1＝50°．
故选：B．
8．【解答】解：由平移的性质可知，AD＝BE＝CF＝3cm，AB＝DE，BC＝EF，AC＝DF，
由于三角形ABC的周长是16cm，即AB+BC+AC＝16cm，
所以四边形ABFD的周长＝AD+AB+BC+CF+DF
＝AB+BC+AC+AD+CF
＝16+3+3
＝22（cm），
故选：D．
9．【解答】解：∵把一张长方形的纸按图那样折叠后，B，C两点落在B1，C1处，
∴∠BEF＝∠B1EF，
∵∠AEB1＝70°，∠AEB1+∠BEF+∠AEB1＝180°，
∴∠BEF＝（180°﹣∠AEB1）＝＝55°．
故选：D．
10．【解答】解：设FBE＝∠FEB＝α，则∠AFE＝2α，
∠FEH的角平分线为EG，设∠GEH＝∠GEF＝β，
∵AD∥BC，∴∠ABC+∠BAD＝180°，
而∠D＝∠ABC，∴∠D+∠BAD＝180°，∴AB∥CD，
∠DEH＝100°，则∠CEH＝∠FAE＝80°，
∠AEF＝180°﹣∠FEG﹣∠HEG＝180°﹣2β，
在△AEF中，80°+2α+180﹣2β＝180°
故β﹣α＝40°，
而∠BEG＝∠FEG﹣∠FEB＝β﹣α＝40°，
故选：B．
二．填空题（共5小题，满分20分，每小题4分）
11．【解答】解：①苹果垂直从树上落下，是平移，
②电梯从底楼升到顶楼，是平移，
③骑自行车时轮胎的滚动，是旋转，
④钟摆的摆动，是旋转，
所以，上列现象是数学中的平移的是：①②，
故答案为：①②．
12．【解答】解：根据题意，∠3的同旁内角是∠6．
故答案为：∠6．
13．【解答】解：如图，过点B作BF∥CD，
∵CD∥AE，
∴CD∥BF∥AE，
∴∠1+∠BCD＝180°，∠2+∠BAE＝180°，
∵∠BCD＝135°，∠BAE＝90°，
∴∠1＝45°，∠2＝90°，
∴∠ABC＝∠1+∠2＝135°．
故答案为：135．
14．【解答】解：由平移的性质知，BE＝CF＝3，DE＝AB＝6，
∴HE＝DE﹣DH＝6﹣2＝4，
∴S四边形HDFC＝S梯形ABEH＝（AB+HE） BE＝（6+4）×3＝15．
故答案为：15．
15．【解答】解：分三种情况：
如图①，AB与CD在EF的两侧时，
∵∠BAF＝110°，∠DCF＝60°，
∴∠ACD＝180°﹣60°﹣（6t）°＝120°﹣（6t）°，∠BAC＝100°﹣t°，
要使AB∥CD，则∠ACD＝∠BAF，
即120°﹣（6t）°＝100°﹣t°，
解得t＝4；
此时（180°﹣60°）÷6＝20，
∴0＜t＜20；
②CD旋转到与AB都在EF的右侧时，
∵∠BAF＝100°，∠DCF＝60°，
∴∠DCF＝360°﹣（6t）°﹣60°＝300°﹣（6t）°，∠BAC＝100°﹣t°，
要使AB∥CD，则∠DCF＝∠BAC，
即300°﹣（6t）°＝100°﹣t°，
解得t＝40，
此时（360°﹣60°）÷6＝50，
∴20＜t＜50；
③CD旋转到与AB都在EF的左侧时，
∵∠BAF＝100°，∠DCF＝60°，
∴∠DCF＝（6t）°﹣（180°﹣60°+180°）＝（6t）°﹣300°，∠BAC＝t°﹣100°，
要使AB∥CD，则∠DCF＝∠BAC，
即（6t）°﹣300°＝t°﹣100°，
解得t＝40，
此时t＞50，
∵40＜50，
∴此情况不存在．
综上所述，当时间t的值为4秒或40秒时，CD与AB平行．
故答案为：4秒或40秒．
三．解答题（共7小题，满分50分）
16．【解答】解：∵直线AC、BC被直线AB所截，
∴∠1 与∠2，∠4 与∠DBC 是同位角；
∠1 与∠3，∠4 与∠5 是内错角；
∠3 与∠4 是同旁内角，∠1 与∠5 是同旁内角．
17．【解答】证明：∵∠BAD＝∠DCB，∠1＝∠3（已知），
∴∠BAD﹣∠1＝∠DCB﹣∠3（等式的性质），
即∠2＝∠4．
∴AD∥BC （内错角相等，两直线平行）．
故答案为：已知，∠1，∠3，∠2，∠4，内错角相等，两直线平行．
18．【解答】解：∵∠1＝∠2，
∴AC∥BD，
∴∠C＝∠BDE，
∵∠B＝∠C，
∴∠B＝∠BDE，
∴AB∥CE．
19．【解答】解：∵∠A＝∠F，
∴AC∥DF，
∴∠C＝∠CEF，
∵∠C＝∠D，
∴∠CEF＝∠D，
∴BD∥CE，
∴∠1＝∠AHC＝55°，
∴∠2＝180°﹣∠AHC＝125°．
20．【解答】证明：（1）∵EB⊥EF，
∴∠FEB＝90°，
∴∠DEF+∠BEG＝180°﹣90°＝90°．
又∵∠EBG+∠BEG＝90°，
∴∠DEF＝∠EBG；
（2）∵∠EBG＝∠A，∠DEF＝∠EBG，
∴∠A＝∠DEF．
∵EF平分∠AED，
∴∠AEF＝∠DEF，
∴∠A＝∠AEF，
∴AB//EF．
21．【解答】（1）解：∵AD∥BE，
∴∠CAD＝∠3，
∵∠2+∠CAE＝∠CAD，∠3＝80°，
∴∠2+∠CAE＝80°，
∵∠2＝30°，
∴∠CAE＝50°；
（2）证明：∵∠2+∠CAE＝∠CAD＝∠3，
∠1＝∠2，∠3＝∠4，
∴∠1+∠CAE＝∠4，
即∠BAE＝∠4，
∴AB∥DC．
22．【解答】解：（1）平行； 理由如下：
∵AC∥BD，MN∥AC，
∴MN∥BD；
（2）∵AC∥BD，MN∥BD，
∴∠PBD＝∠1，∠PAC＝∠2，
∴∠APB＝∠1+∠2＝∠PBD+∠PAC．
（3）答：不成立．
它们的关系是∠APB＝∠PBD﹣∠PAC．
理由是：如图2，过点P作PQ∥AC，
∵AC∥BD，
∴PQ∥AC∥BD，
∴∠PAC＝∠APQ，∠PBD＝∠BPQ，
∴∠APB＝∠BPQ﹣∠APQ＝∠PBD﹣∠PAC．