第1章《平行线》培优训练卷(含解析)

中小学教育资源及组卷应用平台
浙教版2023年第1章《平行线》单元培优训练卷
一．选择题
1．如图，直线AB，CD被直线EF所截，AB∥CD，∠1＝113°，则∠2的度数为（　　）
A．23° B．67° C．77° D．113°
2．如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠2＝40°，则∠1＝（　　）
A．60° B．50° C．40° D．30°
3．下列说法：
①在同一平面内，不相交的两条直线叫做平行线；
②过一点，有且只有一条直线平行于已知直线；
③两条直线被第三条直线所截，同位角相等；
④同旁内角相等，两直线平行．
正确的个数有（　　）个．
A．1 B．2 C．3 D．4
4．如图，从A地到C地有a、b、c三条路可以走，下列判断正确的是（　　）
A．路线a最短 B．路线b最短
C．路线c最短 D．三条路线长度一样长
5．如图，将三角形ABC沿BC方向向右平移3个单位得到△DEF，若四边形ABFD的周长为23，则△ABC的周长为（　　）
A．17 B．18 C．19 D．20
6．如图，AB∥CD，则图中α，β，γ三者之间的关系是（　　）
A．α+β+γ＝180° B．α﹣β+γ＝180° C．α+β﹣γ＝180° D．α+β+γ＝360°
7．如图，已知长方形纸片ABCD，点E，F在AD边上，点G，H在BC边上，分别沿EG，FH折叠，使点D和点A都落在点M处，若α+β＝119°，则∠EMF的度数为（　　）
A．57° B．58° C．59° D．60°
8．如图，直线MN∥PQ，点A在直线MN与PQ之间，点B在直线MN上，连接AB．∠ABM的平分线BC交PQ于点C，连接AC，过点A作AD⊥PQ交PQ于点D，作AF⊥AB交PQ于点F，AE平分∠DAF交PQ于点E，若∠CAE＝45°，∠ACB＝∠DAE，则∠ACD的度数是（　　）
A．18° B．27° C．30° D．45°
二．填空题
9．如图，直线AB∥CD，∠C＝40°，∠E为直角，则∠1＝　 　．
10．生活中常见的探照灯、汽车大灯等灯具都是凹面镜．如图，从光源P点照射到凹面镜上的光线PA、PB等反射以后沿着与直线PF平行的方向射出，若∠CAP＝36°，∠DBP＝58°，则∠APB的度数为 　 　．
11．如图，学生使用的小刀，刀身是长方形，刀片的上下边沿是平行的，刀片转动时会形成∠1和∠2，则∠1+∠2＝　 　．
12．如图，某住宅小区有一长方形地块，若要在长方形地块内修筑同样宽的两条道路，道路宽为2m，余下部分绿化，则绿化的面积为 　 　．
13．如图，防城港市的一条公路修到海边时，需要拐弯绕海而过，如果第一次拐角是∠A＝130°，第二次拐的角是∠B＝160°，第三次拐的角是∠C，这时的道路恰好和第一次拐之前的道路平行，则∠C度数为 　 　．
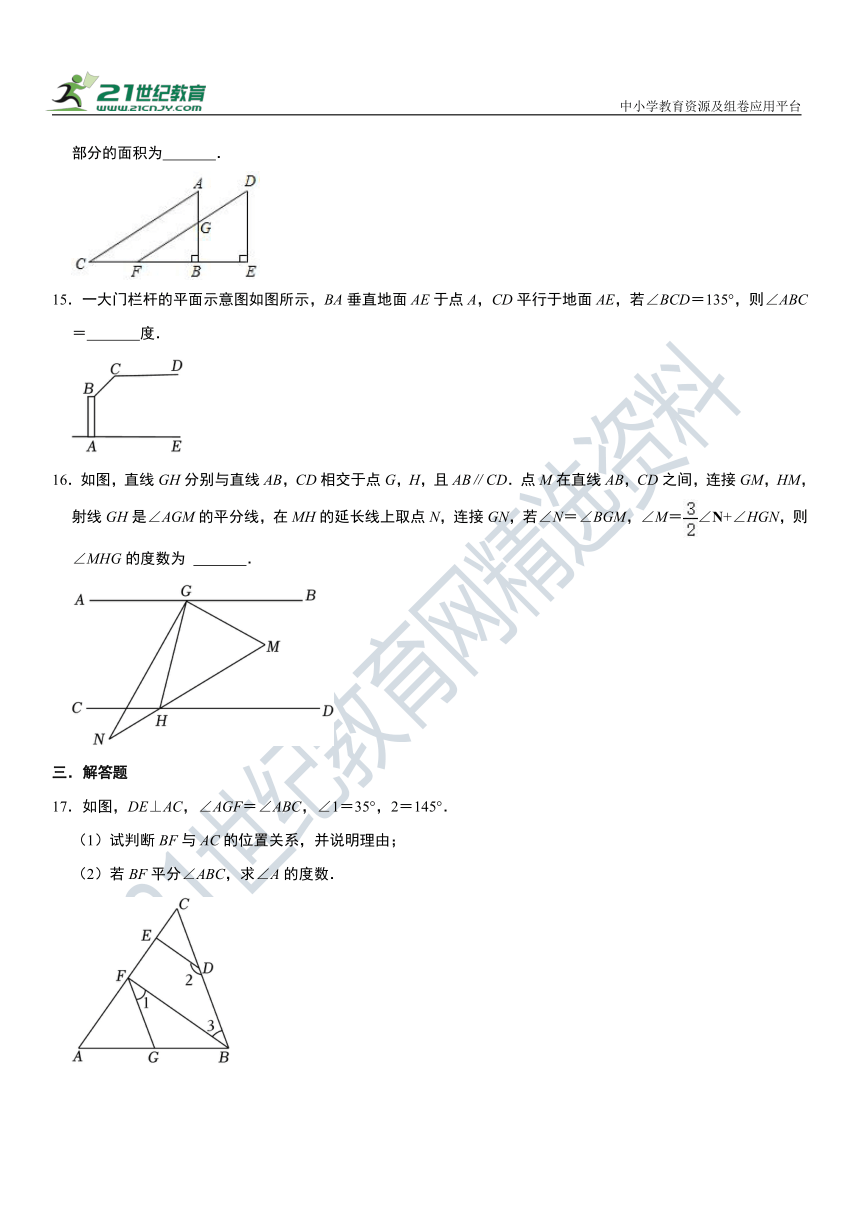
14．如图，将直角三角形ABC沿CB方向平移后，得到直角三角形DEF．已知AG＝3，BE＝6，DE＝10，则阴影部分的面积为　 　．
15．一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD＝135°，则∠ABC＝　 　度．
16．如图，直线GH分别与直线AB，CD相交于点G，H，且AB∥CD．点M在直线AB，CD之间，连接GM，HM，射线GH是∠AGM的平分线，在MH的延长线上取点N，连接GN，若∠N＝∠BGM，∠M＝∠N+∠HGN，则∠MHG的度数为 　 　．
三．解答题
17．如图，DE⊥AC，∠AGF＝∠ABC，∠1＝35°，2＝145°．
（1）试判断BF与AC的位置关系，并说明理由；
（2）若BF平分∠ABC，求∠A的度数．
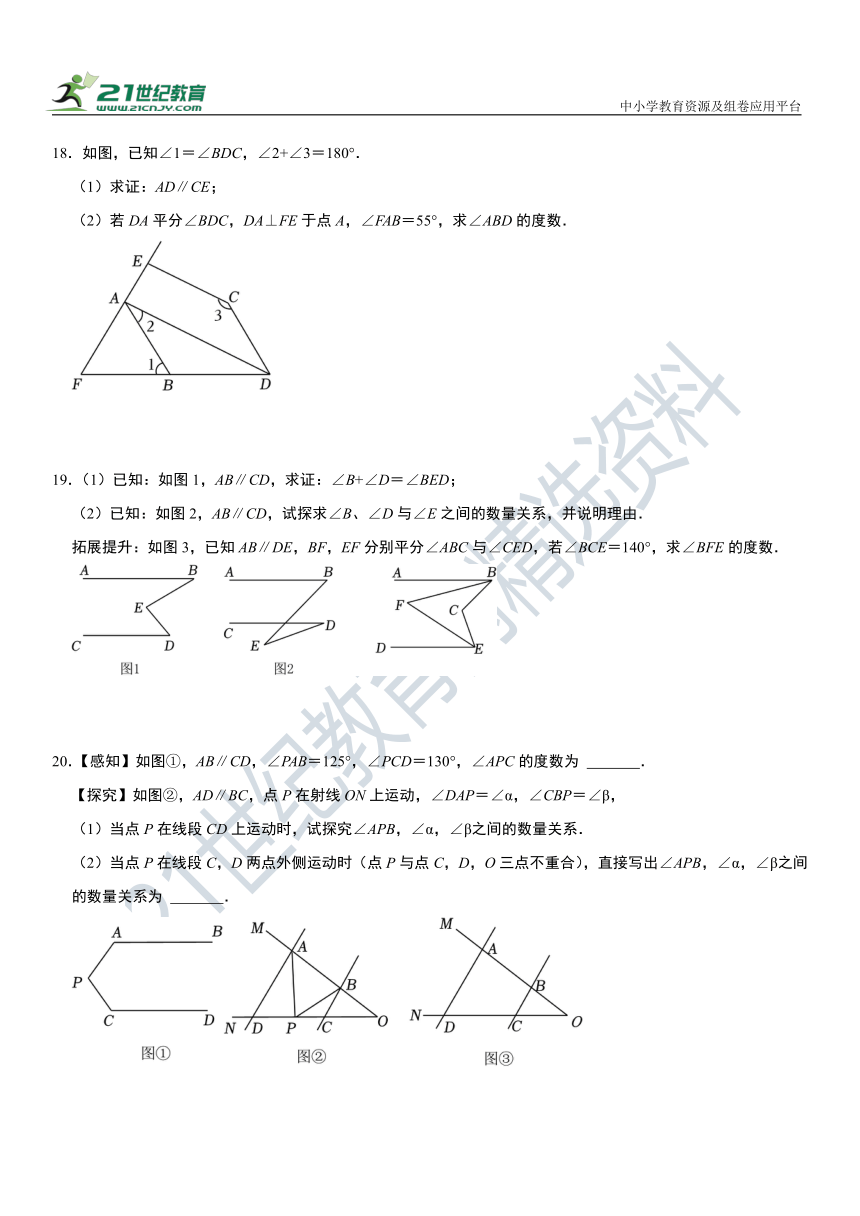
18．如图，已知∠1＝∠BDC，∠2+∠3＝180°．
（1）求证：AD∥CE；
（2）若DA平分∠BDC，DA⊥FE于点A，∠FAB＝55°，求∠ABD的度数．
19．（1）已知：如图1，AB∥CD，求证：∠B+∠D＝∠BED；
（2）已知：如图2，AB∥CD，试探求∠B、∠D与∠E之间的数量关系，并说明理由．
拓展提升：如图3，已知AB∥DE，BF，EF分别平分∠ABC与∠CED，若∠BCE＝140°，求∠BFE的度数．
20．【感知】如图①，AB∥CD，∠PAB＝125°，∠PCD＝130°，∠APC的度数为 　 　．
【探究】如图②，AD∥BC，点P在射线ON上运动，∠DAP＝∠α，∠CBP＝∠β，
（1）当点P在线段CD上运动时，试探究∠APB，∠α，∠β之间的数量关系．
（2）当点P在线段C，D两点外侧运动时（点P与点C，D，O三点不重合），直接写出∠APB，∠α，∠β之间的数量关系为 　 　．
21．（1）问题发现：如图①，直线AB∥CD，连结BE，CE，可以发现∠BEC＝∠B+∠C．
请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∴∠B＝∠BEF（ 　 　）．
∵AB∥DC（已知），EF∥AB，
∴EF∥DC（ 　 　）．
∴∠C＝∠CEF．
∵（ 　 　）＝∠BEF+∠CEF，
∴∠BEC＝∠B+∠C．（等量代换）．
（2）拓展探究：如果点E运动到图②所示的位置，其他条件不变，说明：∠B+∠C＝360°﹣∠BEC．
（3）解决问题：如图③，AB∥DC，E、F、G是AB与CD之间的点，直接写出∠1，∠2，∠3，∠4，∠5之间的数量关系．
22．如图，已知AM∥BN，∠A＝70°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D．
（1）求∠CBD的度数；
（2）当点P运动时，那么∠APB：∠ADB的度数比值是否随之发生变化？若不变，请求出这个比值；若变化，请找出变化规律；
（3）当点P运动到使∠ACB＝∠ABD时，求∠ABC的度数．
参考答案
一．选择题
1．【解答】解：∵AB∥CD，
∴∠CFE＝∠1＝113°，
∠2＝180°﹣∠CFE＝180°﹣113°＝67°，
故选：B．
2．【解答】解：如图，
∵∠2＝40°，
∴∠3＝90°﹣∠2＝50°，
∴∠1＝50°．
故选：B．
3．【解答】解：①在同一平面内，不相交的两条直线叫做平行线，故原命题正确；
②过直线外一点，有且只有一条直线平行于已知直线，故原命题错误；
③两条平行直线被第三条直线所截，同位角相等，故原命题错误；
④同旁内角互补，两直线平行，故原命题错误．
故选：A．
4．【解答】解：根据两点之间线段最短可知，路线b最短．
故选：B．
5．【解答】解：∵将三角形ABC沿边BC方向向右平移3个单位得到三角形DEF，
∴AD＝3，BF＝BC+CF＝BC+3，DF＝AC，
又∵四边形ABFD的周长，
＝AD+AB+BF+DF＝3+AB+BC+3+AC＝23，
∴三角形ABC的周长＝AB+BC+AC＝23﹣6＝17．
故选：A．
6．【解答】解：如图，延长AE交直线CD于F，
∵AB∥CD，
∴∠α+∠AFD＝180°，
∵∠AFD＝∠β﹣∠γ，
∴∠α+∠β﹣∠γ＝180°，
故选：C．
7．【解答】解：∵长方形ABCD，
∴AD∥BC，
∴∠DEG＝α，∠AFH＝β，
∴∠DEG+∠AFH＝α+β＝119°，
由折叠得：∠DEM＝2∠DEG，∠AFM＝2∠AFH，
∴∠DEM+∠AFM＝2×119°＝238°，
∴∠FEM+∠EFM＝360°﹣238°＝122°，
在△EFM中，
∠EMF＝180°﹣（∠FEM+∠EFM）＝180°﹣122°＝58°，
故选：B．
8．【解答】解：设∠DAE＝α，则∠EAF＝α，∠ACB＝α，
∵AD⊥PQ，AF⊥AB，
∴∠BAF＝∠ADE＝90°，
∴∠BAE＝∠BAF+∠EAF＝90°+α，∠CEA＝∠ADE+∠DAE＝90°+α，
∴∠BAE＝∠CEA，
∵MN∥PQ，BC平分∠ABM，
∴∠BCE＝∠CBM＝∠CBA，
又∵∠ABC+∠BCE+∠CEA+∠BAE＝360°，
∴∠BCE+∠CEA＝180°，
∴AE∥BC，
∴∠ACB＝∠CAE，即α＝45°，
∴α＝18°，
∴∠DAE＝18°，
∴Rt△ACD中，∠ACD＝90°﹣∠CAD＝90°﹣（45°+18°）＝27°，
故选：B．
二．填空题
9．【解答】解：过点E作EF∥CD，如图：
则EF∥CD∥AB，
∴∠FEC＝∠DCE＝40°，∠BAE＝∠FEA
∴∠BAE＝∠FEA＝90°﹣∠FEC＝50°，
∴∠1＝180°﹣∠BAE＝130°，
故答案为：130°．
10．【解答】解：∵AC∥EF，∠CAP＝36°，
∴∠APE＝∠CAP＝36°，
∵BD∥EF，∠DBP＝58°，
∴∠BPE＝∠DBP＝58°，
∴∠APB＝∠APE+∠BPE＝94°．
故答案为：94°．
11．【解答】解：如图，过点O作OP∥AB，则∠1＝∠AOP．
∵AB∥CD，OP∥AB，
∴OP∥CD，
∴∠2＝∠POC，
∵∠AOP+∠POC＝90°，
∴∠1+∠2＝90°，
故答案为：90°．
12．【解答】解：由题意得：
（32﹣2）×（20﹣2）
＝30×18
＝540（m2），
∴绿化的面积为540m2，
故答案为：540m2．
13．【解答】解：如图：过B作BD∥AE，
∵BD∥AE，∠A＝130°，
∴∠ABD＝∠A＝130°，
∵∠ABC＝160°，
∴∠DBC＝∠ABC﹣∠ABD＝160°﹣130°＝30°，
∵CF∥AE，
∴BD∥CF，
∴∠C＝180°﹣∠DBC＝150°，
故答案为：150°．
14．【解答】解：由平移的性质知，AB＝DE＝10，S△ABC＝S△DEF，
∵△GBF为△ABC和△DEF的公共部分，
∴S阴影部分＝S梯形DEBG，
∵∠E＝90°，
∴BE是梯形DEBG的高；
∵BG＝AB﹣AG＝10﹣3＝7，
∴S阴影部分＝S梯形DEBG＝×（7+10）×6＝51．
故答案为：51．
15．【解答】解：如图，过点B作BF∥CD，
∵CD∥AE，
∴CD∥BF∥AE，
∴∠1+∠BCD＝180°，∠2+∠BAE＝180°，
∵∠BCD＝135°，∠BAE＝90°，
∴∠1＝45°，∠2＝90°，
∴∠ABC＝∠1+∠2＝135°．
故答案为：135．
16．【解答】解：过M作MF∥AB，过H作HE∥GN，如图：
设∠BGM＝2α，∠MHD＝β，则∠N＝∠BGM＝2α，
∴∠AGM＝180°﹣2α，
∵GH平分∠AGM，
∴∠MGH＝∠AGM＝90°﹣α，
∴∠BGH＝∠BGM+∠MGH＝90°+α，
∵AB∥CD，
∴MF∥AB∥CD，
∴∠M＝∠GMF+∠FMH＝∠BGM+∠MHD＝2α+β，
∵∠M＝∠N+∠HGN，
∴2α+β＝×2α+∠HGN，
∴∠HGN＝β﹣α，
∵HE∥CN，
∴∠GHE＝∠HGN＝β﹣α，∠EHM＝∠N＝2α，
∴∠GHD＝∠GHE+∠EHM+∠MHD＝（β﹣α）+2α+β＝2β+α，
∵AB∥CD，
∴∠BGH+∠GHD＝180°，
∴（90°+α）+（2β+α）＝180°，
∴α+β＝45°，
∴∠MHG＝∠GHE+∠EHM＝（β﹣α）+2α＝α+β＝45°，
故答案为：45°．
三．解答题
17．【解答】解：（1）BF⊥AC，理由如下：
∵∠AGF＝∠ABC，
∴FG∥BC，
∴∠1＝∠3，
∵∠1＝35°，
∴∠3＝35°，
∵∠2＝145°，
∴∠3+∠2＝180°，
∴BF∥DE，
∵DE⊥AC，
∴BF⊥AC；
（2）∵BF平分∠ABC，
∴∠3＝∠ABF＝35°，
∴∠ABC＝70°，
∵DE∥BF，
∴∠CDE＝35°，
∵DE⊥AC，
∴∠CED＝90°，
∴∠C＝55°，
∴∠A＝180°﹣70°﹣55°＝55°．
18．【解答】（1）证明：∵∠1＝∠BDC，
∴AB∥CD，
∴∠2＝∠ADC，
∵∠2+∠3＝180°，
∴∠ADC+∠3＝180°，
∴AD∥CE；
（2）解：∵DA∥CE，DA⊥FE，
∴CE⊥AE于E，
∴∠CEF＝90°，
由（1）知AD∥CE，
∴∠DAF＝∠CEF＝90°，
∴∠ADC＝∠2＝∠DAF﹣∠FAB，
∵∠FAB＝55°，
∴∠ADC＝35°，
∵DA平分∠BDC，∠1＝∠BDC，
∴∠1＝∠BDC＝2∠ADC＝70°
∴∠ABD＝180°﹣70°＝110°．
19．【解答】（1）证明：如图1，过E点作EF∥AB，
则∠1＝∠B，
又∵AB∥CD，
∴EF∥CD，
∴∠B+∠D＝∠1+∠2，
即∠BED＝∠B+∠D．
（2）解：∠B﹣∠D＝∠E，
理由：如图2，过E点作EF∥AB，
则∠BEF＝∠B，
又∵AB∥CD，
∴EF∥CD，
∴∠DEF＝∠CDE，
又∵∠BEF﹣∠DEF＝∠BED，
∴∠B﹣∠CDE＝∠BED；
（3）解：如图，过点C作CP∥AB，则∠BCP＝∠ABC，∠ECP＝∠CED，
∴∠ABC+∠CED＝∠BCP+∠ECP＝∠BCE＝140°；
又∵BF，EF分别平分∠ABC，∠CED，
∴∠ABF＝∠ABC，∠DEF＝∠DEC；
∴∠ABF+∠DEF＝（∠ABC+∠DEC）＝70°，
过点F作FM∥DE，则∠BFM＝∠ABF，∠MFE＝∠DEF，
∴∠BFE＝∠BFM+∠MFE＝∠ABF+∠DEF＝70°．
20．【解答】【感知】解：过P作PE∥AB，
∵AB∥CD，
∴PQ∥AB∥CD，
∴∠APQ＝180°﹣∠PAB＝55°，∠CPQ＝180°﹣∠PCD＝50°，
∴∠APC＝50°+55°＝105°；
故答案为：105°；
【探究】解：（1）∠APB＝∠α+∠β，理由如下：
如图②，过P作PE∥AD交AB于E，
∵AD∥BC，
∴AD∥PE∥BC，
∴∠α＝∠APE，∠β＝∠BPE，
∴∠APB＝∠APE+∠BPE＝∠α+∠β；
（2）当点P在D、N两点之间时，∠APB∠β﹣∠α；
理由：如图③，过P作PE∥AD交AB于E，
∵AD∥BC，
∴AD∥PE∥BC，
∴∠α＝∠APE，∠β＝∠BPE，
∴∠APB＝∠BPE﹣∠APE＝∠β﹣∠α；
当点P在C、O两点之间时，∠APB＝∠α﹣∠β．
理由：如图④，过P作PE∥AD交AB于E点，
∵AD∥BC，
∴AD∥PE∥BC，
∴∠α＝∠APE，∠β＝∠BPE，
∴∠APB＝∠APE﹣∠BPE＝∠α﹣∠β．
故答案为：当点P在D、N两点之间时，∠APB＝∠β﹣∠α；当点P在C、O两点之间时，∠APB＝∠α﹣∠β．
21．【解答】（1）证明：过点E作EF∥AB，
∴∠B＝∠BEF（两直线平行，内错角相等）．
∵AB∥DC（已知），EF∥AB，
∴EF∥DC（平行于同一直线的两直线平行）．
∴∠C＝∠CEF．
∵（∠B+∠C）＝∠BEF+∠CEF，
∴∠BEC＝∠B+∠C．（等量代换），
故答案为：两直线平行，内错角相等，平行于同一直线的两直线平行，∠B+∠C；
（2）解：如图②，过点E作EF∥AB，
∵AB∥CD，EF∥AB，
∴EF∥CD，
∴∠C+∠CEF＝180°，∠B+∠BEF＝180°，
∴∠B+∠C+∠AEC＝360°，
∴∠B+∠C＝360°﹣（∠BEF+∠CEF），
即∠B+∠C＝360°﹣∠BEC；
（3）解：∠1+∠3+∠5＝∠2+∠4，理由如下：
如图，过点F作FM∥AB，则AB∥FM∥CD，
由（1）得，∠1+∠3+∠5＝∠2+∠4．
22．【解答】解：（1）∵AM∥BN，
∴∠ABN+∠A＝180°，
∴∠ABN＝180°﹣70°＝110°，
∴∠ABP+∠PBN＝110°，
∵BC平分∠ABP，BD平分∠PBN，
∴∠ABP＝2∠CBP，∠PBN＝2∠DBP，
∴2∠CBP+2∠DBP＝110°，
∴∠CBD＝∠CBP+∠DBP＝55°；
（2）不变，∠APB：∠ADB＝2：1，理由如下：
∵AM∥BN，
∴∠APB＝∠PBN，∠ADB＝∠DBN，
∵BD平分∠PBN，
∴∠PBN＝2∠DBN，
∴∠APB：∠ADB＝2：1；
（3）∵AM∥BN，
∴∠ACB＝∠CBN，
∵∠ACB＝∠ABD，
∴∠CBN＝∠ABD，
∴∠CBN﹣∠CBD＝∠ABD﹣∠CBD，
∴∠DBN＝∠ABC，
由（1）可知∠ABN＝110°，∠CBD＝55°，
∴∠ABC+∠DBN＝55°，
∴∠ABC＝27.5°．