3.4乘法公式（1）

课件14张PPT。多项式乘法法则是:用一个多项式的每一项乘另一个多项式的每一项再把所得的积相加。
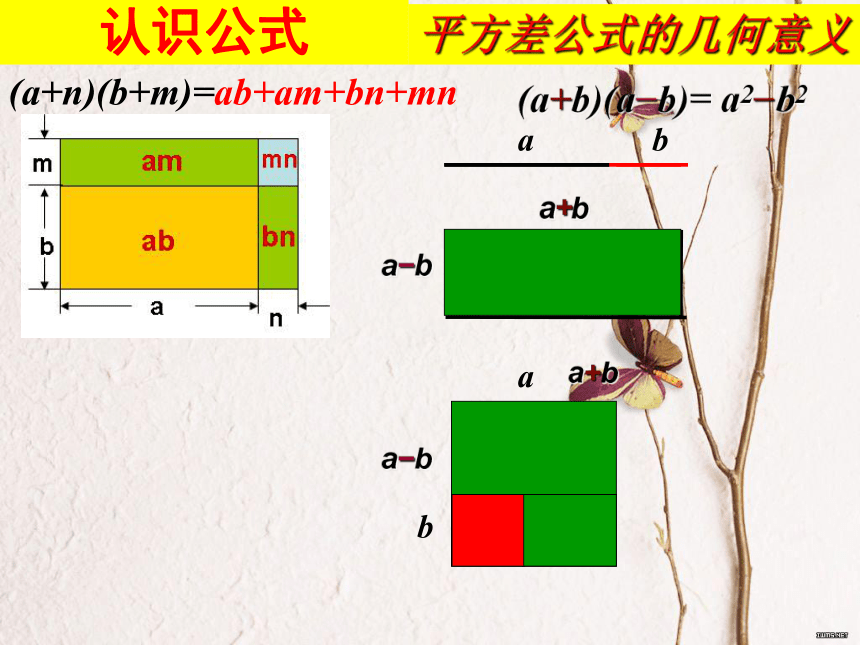
(m+a)(n+b)=mn+mb+an+ab 如果m=n，且都用 x 表示，那么上式就成为:=(x+a)(x+b)x2+(a+b)x+ab 两个相同字母的二项式的乘积 .(m+a)(n+b)=mn+mb+an+ab =(x+a)(x+b)x2+(a+b)x+ab a、b互为相反数a、b相同能否更特殊?特殊化：第一项相同(x+a)(x-a)=x2-a2(a+b)(a-b)=a2-b23.4乘法公式（1）(m+a)(n+b)=mn+mb+an+ab (x+a)(x+b) = x2+(a+b)x+ab (a+b)(a-b) = a2-b2(3) (x+3)(x?3) (4) (1? 2a)(1+2a)(5) (3x+7)(3x?7) (2) (x+5)(x?3) (1) (2x+3y)(x?2y) = 2x2 －xy－6y2= x2 +2x－15= x2 －9= 1－4a2= 9x2 －49=x2?32 ;= 12－(2a)2= (3x)2 －72探究公式两数和与这两数差的积,等于这两数的平方差.(a+b)(a-b) = a2-b2认识公式平方差公式(3) (x+3)(x?3) (4) (1? 2a)(1+2a)(5) (3x+7)(3x?7) =x2?32 ;= 12－(2a)2= (3x)2 －72公式中的 a和b 可以代表数，也可以是代数式． 左边两括号内的第一项相等第二项符号相反[互为相反数];右边是左边括号内的第一项的平方减去第二项的平方.(a+b)(a?b)= a2?b2认识公式(a+n)(b+m)=ab+am+bn+mnaba+ba?bab平方差公式的几何意义a+ba?b认识公式下列可以用平方差公式计算的是( )(1) (x－y)(x+y)(2) (－x－y)(－x+ y)(3) (x－y)(－y+x)(4) (x－y)(－x+y)（5) （a+b-c)(a+b+c)（8) （a-b-c)(-a+b+c)（7) （-a+b-c)(-a+b-c)（6) （a-b+c)(a+b-c)一项相同,另一项相反一项相同,两项相反
一项相反,两项相同三项相同或三项相反适用不适用两项相同或两项相反(a+b)(a?b)= a2?b2.步骤：(3a2-7)(-3a2-7) （注意点：要用好括号；幂的运算。）当某一项是一分数或是数与字母的乘积时,要用括号把这个数整个括起来，最后的结果又要用相关的幂的运算去掉括号。应用公式1、判断；2、调整；3、分步解。(a+b)(a?b)= a2?b2.下列可以用平方差公式计算的是( )(a+b)(a?b)= a2?b2.应用公式－14a(－1)2－(4a)21－16a2(a+b)(a?b)= a2?b2.应用公式简便计算:(a+b)(a?b)= a2?b2.应用公式计算:其中知识梳理一、探究公式二、认识公式三、应用公式(m+a)(n+b)=mn+mb+an+ab =(x+a)(x+b)x2+(a+b)x+ab (a+b)(a-b)=a2-b2平方差公式的几何意义平方差公式的结构特征计算化简简便计算连用公式增项配公式位置变化符号变化系数变化项数变化巩固训练其中会识别判断下列算式能否用平方差公式计算,并转化成平方差公式的形式（1)（-a+b)(a+b)

(2) (-2a+b)(-2a-b)
(3) (-a+b)(a-b)

(4) (a+b)(a-c)（能） （否）（否）（能）(a+b)(a?b)= a2?b2.