3.1 同底数幂的乘法 课件(共19张PPT)
文档属性
| 名称 | 3.1 同底数幂的乘法 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 21:22:15 | ||
图片预览






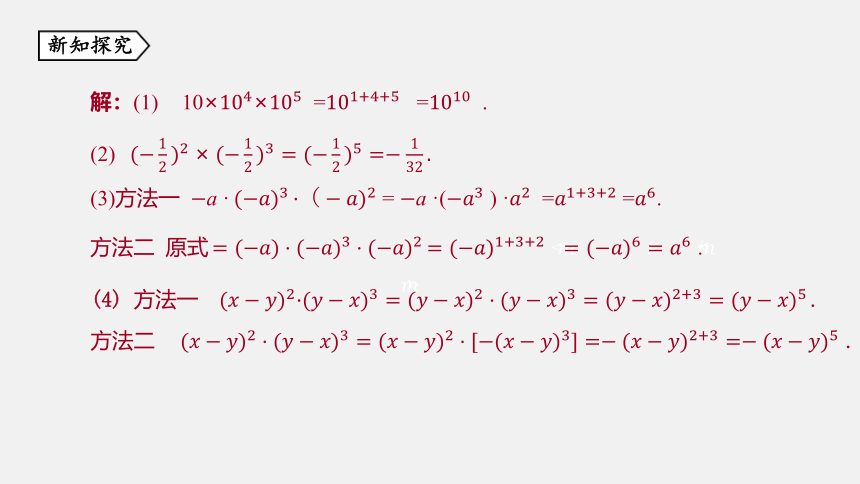
文档简介
(共19张PPT)
第3章 整式的乘除
3.1 同底数幂的乘法
学习目标
1.理解同底数幂的乘法、幂的乘方、积的乘方法则,并能逆用法则.
2.会运用同底数幂的乘法法则进行同底数幂相乘,并解决简单的实际问题.
3.会运用幂的乘方法则计算幂的乘方.
4.会计算积的乘方.
5.会综合运用同底数幂的乘法法则、幂的乘方法则和积的乘方法则进行幂的混合运算.
知识点1 同底数幂的乘法 重点
1.同底数幂的乘法法则的推导过程:
同底数幂相乘
2.同底数幂的乘法法则:
文字叙述 同底数幂相乘,底数不变,指数相加.
字母表示
逆用
运用的条件 运用同底数幂的乘法法则必须满足两个条件:(1)底数相同;(2)是乘法运算.
示例 同底数幂的乘法
深挖教材
幂的运算中常见的拓展应用
(1)同底数幂的乘法法则的推广:同底数幂的乘法法则也适用于三个或三个以上的同底数幂相乘,即
(2)在幂的运算中,经常用到以下变形:
典例1 计算下列各式.
(1)
(2)
(3)
(4)
(3)方法一 a · = a ·( ) · = =.
方法二 原式
<
解:(1) 10×× = = .
(2)
(4) 方法一.
方法二
知识点2 幂的乘方 重点
1.幂的乘方法则的推导过程:
幂的乘方法则的逆用
2.幂的乘方法则:
文字叙述 幂的乘方,底数不变,指数相乘.
字母表示
推广
逆用
典例2 计算下列各式,结果用幂的形式表示.
(1)
解:(1)
(2)
(2)
(3)
(3)
(4)
(4)
知识点3 积的乘方 重点
1.积的乘方法则的推导过程:
2.积的乘方法则:
文字叙述 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
字母表示
推广
逆用
辨析
同底数幂的乘法法则、幂的乘方法则和积的乘方法则的区别
运算法则 运算特点 公式
同底数幂的乘法 底数不变 指数相加
幂的乘方 指数相乘
积的乘方 底数中的每个因式分别乘方,再把幂相乘
典例3 计算下列各式:
(1)
解:(1) · = 27.
(2)
(3)
(3)
(4)
(4)
(2)
(1)
本节知识归纳
中考常考考点 难度 常考题型
考点1:同底数幂的乘法,常与幂的乘方、积的乘方或以后学习的整式的乘法综合运用.
考点2:幂的乘方,常逆用求值或与同底数幂的乘法、积的乘方综合考查.
考点3:积的乘方,常逆用求值或与同底数幂的乘法、幂的乘方综合考查.
考点1 同底数幂的乘法
典例4 [2022·丽水中考] 计算
A.
C
[解析]
链接教材 本题取材于教材第60页例1,考查了同底数幂的乘法,属于基础题.解题的关键是:(1)正确判断幂的运算类型;(2)注意符号与指数的变化.
考点2 幂的乘方
典例5 [2022·成都中考] 计算:
[解析]
链接教材 本题取材于教材第63页例3,考查了幂的乘方,属于基础题.
考点3 积的乘方
典例6 [黄石中考] 计算
A.
B
[解析]
链接教材 本题取材于教材第65页例4,考查了积的乘方,属于基础题.考查积的乘方时往往会综合考查幂的乘方,求解时注意符号的变化.
第3章 整式的乘除
3.1 同底数幂的乘法
学习目标
1.理解同底数幂的乘法、幂的乘方、积的乘方法则,并能逆用法则.
2.会运用同底数幂的乘法法则进行同底数幂相乘,并解决简单的实际问题.
3.会运用幂的乘方法则计算幂的乘方.
4.会计算积的乘方.
5.会综合运用同底数幂的乘法法则、幂的乘方法则和积的乘方法则进行幂的混合运算.
知识点1 同底数幂的乘法 重点
1.同底数幂的乘法法则的推导过程:
同底数幂相乘
2.同底数幂的乘法法则:
文字叙述 同底数幂相乘,底数不变,指数相加.
字母表示
逆用
运用的条件 运用同底数幂的乘法法则必须满足两个条件:(1)底数相同;(2)是乘法运算.
示例 同底数幂的乘法
深挖教材
幂的运算中常见的拓展应用
(1)同底数幂的乘法法则的推广:同底数幂的乘法法则也适用于三个或三个以上的同底数幂相乘,即
(2)在幂的运算中,经常用到以下变形:
典例1 计算下列各式.
(1)
(2)
(3)
(4)
(3)方法一 a · = a ·( ) · = =.
方法二 原式
<
解:(1) 10×× = = .
(2)
(4) 方法一
方法二
知识点2 幂的乘方 重点
1.幂的乘方法则的推导过程:
幂的乘方法则的逆用
2.幂的乘方法则:
文字叙述 幂的乘方,底数不变,指数相乘.
字母表示
推广
逆用
典例2 计算下列各式,结果用幂的形式表示.
(1)
解:(1)
(2)
(2)
(3)
(3)
(4)
(4)
知识点3 积的乘方 重点
1.积的乘方法则的推导过程:
2.积的乘方法则:
文字叙述 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
字母表示
推广
逆用
辨析
同底数幂的乘法法则、幂的乘方法则和积的乘方法则的区别
运算法则 运算特点 公式
同底数幂的乘法 底数不变 指数相加
幂的乘方 指数相乘
积的乘方 底数中的每个因式分别乘方,再把幂相乘
典例3 计算下列各式:
(1)
解:(1) · = 27.
(2)
(3)
(3)
(4)
(4)
(2)
(1)
本节知识归纳
中考常考考点 难度 常考题型
考点1:同底数幂的乘法,常与幂的乘方、积的乘方或以后学习的整式的乘法综合运用.
考点2:幂的乘方,常逆用求值或与同底数幂的乘法、积的乘方综合考查.
考点3:积的乘方,常逆用求值或与同底数幂的乘法、幂的乘方综合考查.
考点1 同底数幂的乘法
典例4 [2022·丽水中考] 计算
A.
C
[解析]
链接教材 本题取材于教材第60页例1,考查了同底数幂的乘法,属于基础题.解题的关键是:(1)正确判断幂的运算类型;(2)注意符号与指数的变化.
考点2 幂的乘方
典例5 [2022·成都中考] 计算:
[解析]
链接教材 本题取材于教材第63页例3,考查了幂的乘方,属于基础题.
考点3 积的乘方
典例6 [黄石中考] 计算
A.
B
[解析]
链接教材 本题取材于教材第65页例4,考查了积的乘方,属于基础题.考查积的乘方时往往会综合考查幂的乘方,求解时注意符号的变化.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
