4.3 用乘法公式分解因式 课件(共20张PPT)
文档属性
| 名称 | 4.3 用乘法公式分解因式 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 21:30:24 | ||
图片预览








文档简介
(共20张PPT)
第4章 因式分解
4.3 用乘法公式分解因式
学习目标
1.会用平方差公式、完全平方公式分解因式.
2.了解因式分解的思考步骤.
3.会综合运用提取公因式法与公式法(平方差公式、完全平方公式)分解因式.
知识点1 用平方差公式分解因式 重点
公式
文字叙述 两个数的平方差,等于这两个数的和与这两个数的差的积.
能用平方差公式分解因式的多项式的特征 (1)只有两项(或两个整体);
(2)两项都能用完全平方表示,即字母的指数是偶数,系数是完全平方数;
(3) 两项符号相反(一项为正,一项为负).
注意 公式中的
示例1 用平方差公式分解因式 .
典例1 下列多项式中,能用平方差公式分解因式的是( )
A.
D
[解析]
选项 分析 结论
A
B
C
D
典例2 把下列各式因式分解:
(1)
解:(1)
(2)
(2)
(3)
(3)
< .
(4)
(4)
例题点拨
分解因式要彻底,分解到不能再分解为止,如本题(4)易错误认为分解的最后结果是
知识点2 用完全平方公式分解因式重点
1.完全平方式:我们把多项式
简记为:
①
2.
公式
文字叙述 两数的平方和,加上(或者减去)这两数的积的2倍,等于这两数和(或者差)的平方.
能用完全平方公式分解因式的多项式的特征 符合完全平方式,即(1)多项式是三项;
(2)要有两个符号相同的平方项和一个交叉项;
(3)交叉项要等于两个平方项底数的积的2倍.
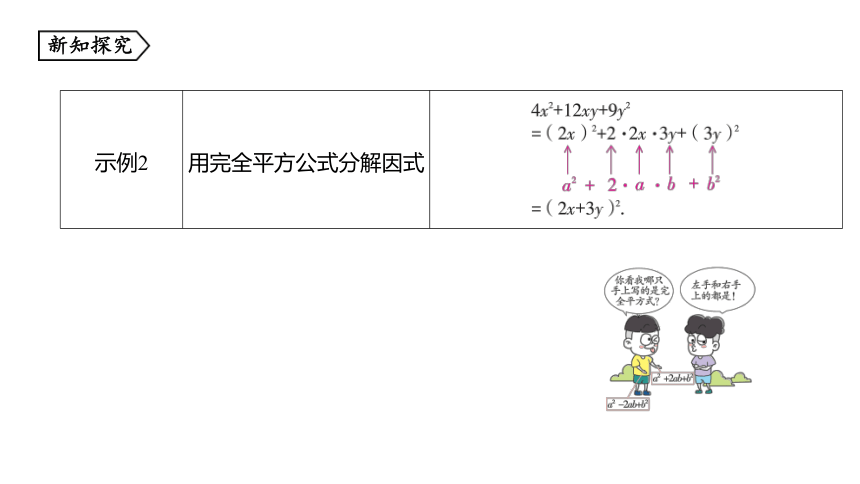
示例2 用完全平方公式分解因式
3.公式法:一般地,利用公式
典例3 下列各式中,能用完全平方公式分解因式的是( )
A.
C
[解析]
选项 分析 结论
A
B
C
D
典例4 把下列各式因式分解:
(1)
解:(1)
(2)
(2)
(3)
(3)
(4)
(4)(x+2)2+6(x+2)+9=(x+2)2+2(x+2)·3+32=(x+2+3)2=(x+5)2. &2&
例题点拨
运用完全平方公式分解因式的步骤
知识点3 用提取公因式法和公式法分解因式
因式分解的一般步骤:
典例5 把下列各式分解因式:
(1)
解:(1)
(2)
(2)
(3)
(3)
本节知识归纳
中考常考考点 难度 常考题型
考点1:用公式法分解因式.
考点2:综合运用提取公因式法和公式法分解因式.
考点1 用公式法分解因式
典例6 [杭州中考] 因式分解:
A.
C.
A
[解析]
链接教材 本题取材于教材第103页例1,考查了运用平方差公式分解因式.解题的关键是将多项式化为
典例7 [2022·宁波中考] 分解因式:
[解析]
链接教材 本题取材于教材第106页例3,考查了运用完全平方公式分解因式.解此类题的关键是将多项式化为
考点2 综合运用提取公因式法和公式法分解因式
典例8 因式分解:
(1)[2022·绵阳中考]
[解析] (1) 原式
(2)[2022·沈阳中考]
(2) 原式
链接教材 本题取材于教材第108页作业题第6题,考查了运用提取公因式法和公式法分解因式.对于此类问题的求解,有公因式的要先提取公因式,提取公因式后,再考虑用公式法分解因式.
第4章 因式分解
4.3 用乘法公式分解因式
学习目标
1.会用平方差公式、完全平方公式分解因式.
2.了解因式分解的思考步骤.
3.会综合运用提取公因式法与公式法(平方差公式、完全平方公式)分解因式.
知识点1 用平方差公式分解因式 重点
公式
文字叙述 两个数的平方差,等于这两个数的和与这两个数的差的积.
能用平方差公式分解因式的多项式的特征 (1)只有两项(或两个整体);
(2)两项都能用完全平方表示,即字母的指数是偶数,系数是完全平方数;
(3) 两项符号相反(一项为正,一项为负).
注意 公式中的
示例1 用平方差公式分解因式 .
典例1 下列多项式中,能用平方差公式分解因式的是( )
A.
D
[解析]
选项 分析 结论
A
B
C
D
典例2 把下列各式因式分解:
(1)
解:(1)
(2)
(2)
(3)
(3)
(4)
(4)
例题点拨
分解因式要彻底,分解到不能再分解为止,如本题(4)易错误认为分解的最后结果是
知识点2 用完全平方公式分解因式重点
1.完全平方式:我们把多项式
简记为:
①
2.
公式
文字叙述 两数的平方和,加上(或者减去)这两数的积的2倍,等于这两数和(或者差)的平方.
能用完全平方公式分解因式的多项式的特征 符合完全平方式,即(1)多项式是三项;
(2)要有两个符号相同的平方项和一个交叉项;
(3)交叉项要等于两个平方项底数的积的2倍.
示例2 用完全平方公式分解因式
3.公式法:一般地,利用公式
典例3 下列各式中,能用完全平方公式分解因式的是( )
A.
C
[解析]
选项 分析 结论
A
B
C
D
典例4 把下列各式因式分解:
(1)
解:(1)
(2)
(2)
(3)
(3)
(4)
(4)(x+2)2+6(x+2)+9=(x+2)2+2(x+2)·3+32=(x+2+3)2=(x+5)2. &2&
例题点拨
运用完全平方公式分解因式的步骤
知识点3 用提取公因式法和公式法分解因式
因式分解的一般步骤:
典例5 把下列各式分解因式:
(1)
解:(1)
(2)
(2)
(3)
(3)
本节知识归纳
中考常考考点 难度 常考题型
考点1:用公式法分解因式.
考点2:综合运用提取公因式法和公式法分解因式.
考点1 用公式法分解因式
典例6 [杭州中考] 因式分解:
A.
C.
A
[解析]
链接教材 本题取材于教材第103页例1,考查了运用平方差公式分解因式.解题的关键是将多项式化为
典例7 [2022·宁波中考] 分解因式:
[解析]
链接教材 本题取材于教材第106页例3,考查了运用完全平方公式分解因式.解此类题的关键是将多项式化为
考点2 综合运用提取公因式法和公式法分解因式
典例8 因式分解:
(1)[2022·绵阳中考]
[解析] (1) 原式
(2)[2022·沈阳中考]
(2) 原式
链接教材 本题取材于教材第108页作业题第6题,考查了运用提取公因式法和公式法分解因式.对于此类问题的求解,有公因式的要先提取公因式,提取公因式后,再考虑用公式法分解因式.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
