5.5 分式方程 课件(共21张PPT)
文档属性
| 名称 | 5.5 分式方程 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 22:11:09 | ||
图片预览








文档简介
(共21张PPT)
第5章 分式
5.5 分式方程
学习目标
1.了解分式方程的概念.
2.会解可化为一元一次方程的分式方程.
3.了解增根的概念,会对分式方程的根进行检验.
4.会列分式方程解简单应用题.
5.会进行简单的公式变形.
知识点1 分式方程的概念
1.分式方程:只含分式,或分式和整式,并且分母里含有未知数的方程叫做分式方程.
2.分式方程包含两个条件:①只含分式,或分式和整式;②分母中含有未知数.两个条件缺一不可.
例如:方程
辨析
分式方程和整式方程的区别与联系
分式方程 整式方程
区别 分母中含有未知数. 分母中不含未知数.
联系 分式方程可以转化为整式方程. 典例1 下列式子:①
A.1个 B.2 个 C.3个 D.4个
A
解析:
序号 分析 结论
① 是方程,但该方程的分母中不含未知数. 不是分式方程.
② 满足分式方程的定义. 是分式方程.
③ 不是方程. 不是分式方程.
④ 不满足只含分式或分式和整式. 不是分式方程.
⑤ 是方程,但该方程的分母中不含未知数. 不是分式方程.
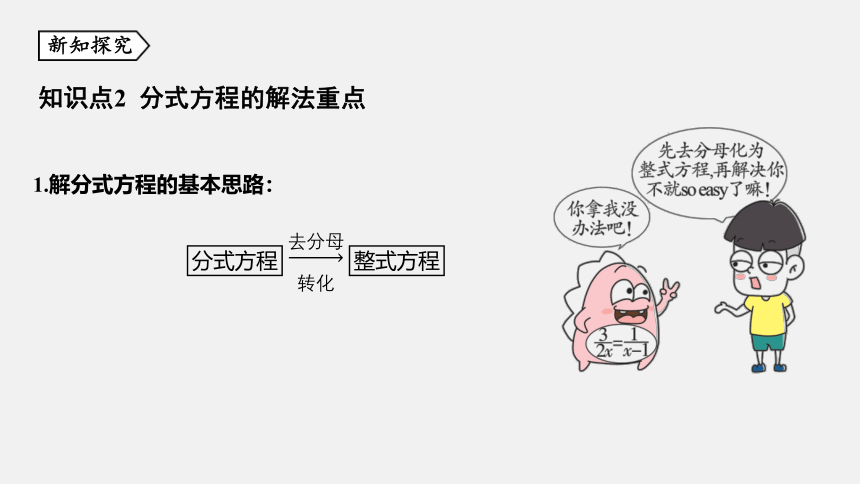
知识点2 分式方程的解法重点
1.解分式方程的基本思路:
2.解可化为一元一次方程的分式方程的一般步骤:
步骤 方法
一去分母 方程两边同乘公分母,把分式方程转化为一元一次方程.
二解 解该一元一次方程.
三检验 ①代入原方程,看方程是否成立;
②代入原方程两边所乘的公分母,看分母的值是否为零,使分母为零的根不是原方程的根.
四写 写出原分式方程的根或无解.
教材深挖
分式方程无解问题的情况
分式方程去分母后,若所得的整式方程的根使原分式方程的公分母为零,
则原分式方程无解;
若所得的整式方程是
则整式方程无解,即原分式方程无解.
反之,若原分式方程无解,则同样可以得到所得的整式方程
的根使得原分式方程的公分母为零或所得的整式方程无解两
种情况.
典例2 解下列方程:
(1)
解:方程两边同乘
解方程,得
将
所以
(2)
解:方程两边同乘以
解方程,得
把
所以
知识点3 分式方程的增根 难点
1.增根:分式方程去分母转化为整式方程,若整式方程的根使分母为零,
这种根叫做原方程的增根.
2.增根满足两个条件:①是整式方程的根;②使分母的值为零.
3.产生增根的原因:去分母时,方程两边同乘的公分母是含有
未知数的整式,这个整式有可能为零,对于整式方程来说,求
出的根成立,而对于原分式方程来说,分式无意义,所以这个
根是原分式方程的增根.
典例3 关于
则
A.
C.
D
解析: 方程两边同乘
因为方程有增根,
例题点拨
由分式方程的根的情况
求字母的值的方法
知识点4 分式方程的应用 重难点
列分式方程解应用题的一般步骤:
(1)审:了解已知数与所求各量所表示的意义,弄清它们之间的数量关系;
(2)设:设未知数;
(3)列:找出能够表示题中全部含义的相等关系,列出分式方程;
(4)解:解这个分式方程;
(5)验:检验所求的根是不是增根,是否符合题意;
(6)答:写出答案.
敲黑板
(1)审题时,先寻找题目中的关键词,然后借助列表、画图等方法准确找出相等关系.当题目中包含多个相等关系时,要选择一个能够体现全部(或大部分)数量的相等关系列方程.
(2)设未知数时,一般题中问什么就设什么,即设直接未知数;若设直接未知数难以列方程,则可设另一个相关量为未知数,即设间接未知数;有时设一个未知数无法表示等量关系,可设多个未知数,即设辅助未知数.
典例4 甲、乙两班参加绿化校园植树活动,已知乙班每小时比甲班多种2棵树,甲班种60棵树所用的时间与乙班种66棵树所用的时间相等.求甲、乙两班每小时各种多少棵树.
解:设甲班每小时种
由题意可得
解这个方程,得
经检验,
答:甲班每小时种20棵树,乙班每小时种22棵树.
本节知识归纳
考点1 解分式方程
典例5 [2022·嘉兴中考] 解方程:
解:两边同乘
解得
经检验,当
所以
中考常考考点 难度 常考题型
考点1:解分式方程. ★★ 填空题、解答题
考点2:分式方程的实际应用. ★★★★ 选择题、解答题
考点2 分式方程的实际应用
典例6 [嘉兴中考] 为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为
A.
B
解析:∵荧光棒的单价为
根据题意,得
典例7 [湖州中考] 某企业承接了27 000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产.
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
解:(1)设甲车间有
由题意,得
解得
答:甲车间有30名工人参与生产,乙车间有20名工人参与生产.
①求乙车间需临时招聘的工人数.
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1 500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
(2)①设方案二中乙车间需临时招聘
由题意,得
经检验,
∴乙车间需临时招聘5名工人.
②企业完成生产任务所需的时间为
∴选择方案一需增加的费用为
选择方案二需增加的费用为
第5章 分式
5.5 分式方程
学习目标
1.了解分式方程的概念.
2.会解可化为一元一次方程的分式方程.
3.了解增根的概念,会对分式方程的根进行检验.
4.会列分式方程解简单应用题.
5.会进行简单的公式变形.
知识点1 分式方程的概念
1.分式方程:只含分式,或分式和整式,并且分母里含有未知数的方程叫做分式方程.
2.分式方程包含两个条件:①只含分式,或分式和整式;②分母中含有未知数.两个条件缺一不可.
例如:方程
辨析
分式方程和整式方程的区别与联系
分式方程 整式方程
区别 分母中含有未知数. 分母中不含未知数.
联系 分式方程可以转化为整式方程. 典例1 下列式子:①
A.1个 B.2 个 C.3个 D.4个
A
解析:
序号 分析 结论
① 是方程,但该方程的分母中不含未知数. 不是分式方程.
② 满足分式方程的定义. 是分式方程.
③ 不是方程. 不是分式方程.
④ 不满足只含分式或分式和整式. 不是分式方程.
⑤ 是方程,但该方程的分母中不含未知数. 不是分式方程.
知识点2 分式方程的解法重点
1.解分式方程的基本思路:
2.解可化为一元一次方程的分式方程的一般步骤:
步骤 方法
一去分母 方程两边同乘公分母,把分式方程转化为一元一次方程.
二解 解该一元一次方程.
三检验 ①代入原方程,看方程是否成立;
②代入原方程两边所乘的公分母,看分母的值是否为零,使分母为零的根不是原方程的根.
四写 写出原分式方程的根或无解.
教材深挖
分式方程无解问题的情况
分式方程去分母后,若所得的整式方程的根使原分式方程的公分母为零,
则原分式方程无解;
若所得的整式方程是
则整式方程无解,即原分式方程无解.
反之,若原分式方程无解,则同样可以得到所得的整式方程
的根使得原分式方程的公分母为零或所得的整式方程无解两
种情况.
典例2 解下列方程:
(1)
解:方程两边同乘
解方程,得
将
所以
(2)
解:方程两边同乘以
解方程,得
把
所以
知识点3 分式方程的增根 难点
1.增根:分式方程去分母转化为整式方程,若整式方程的根使分母为零,
这种根叫做原方程的增根.
2.增根满足两个条件:①是整式方程的根;②使分母的值为零.
3.产生增根的原因:去分母时,方程两边同乘的公分母是含有
未知数的整式,这个整式有可能为零,对于整式方程来说,求
出的根成立,而对于原分式方程来说,分式无意义,所以这个
根是原分式方程的增根.
典例3 关于
则
A.
C.
D
解析: 方程两边同乘
因为方程有增根,
例题点拨
由分式方程的根的情况
求字母的值的方法
知识点4 分式方程的应用 重难点
列分式方程解应用题的一般步骤:
(1)审:了解已知数与所求各量所表示的意义,弄清它们之间的数量关系;
(2)设:设未知数;
(3)列:找出能够表示题中全部含义的相等关系,列出分式方程;
(4)解:解这个分式方程;
(5)验:检验所求的根是不是增根,是否符合题意;
(6)答:写出答案.
敲黑板
(1)审题时,先寻找题目中的关键词,然后借助列表、画图等方法准确找出相等关系.当题目中包含多个相等关系时,要选择一个能够体现全部(或大部分)数量的相等关系列方程.
(2)设未知数时,一般题中问什么就设什么,即设直接未知数;若设直接未知数难以列方程,则可设另一个相关量为未知数,即设间接未知数;有时设一个未知数无法表示等量关系,可设多个未知数,即设辅助未知数.
典例4 甲、乙两班参加绿化校园植树活动,已知乙班每小时比甲班多种2棵树,甲班种60棵树所用的时间与乙班种66棵树所用的时间相等.求甲、乙两班每小时各种多少棵树.
解:设甲班每小时种
由题意可得
解这个方程,得
经检验,
答:甲班每小时种20棵树,乙班每小时种22棵树.
本节知识归纳
考点1 解分式方程
典例5 [2022·嘉兴中考] 解方程:
解:两边同乘
解得
经检验,当
所以
中考常考考点 难度 常考题型
考点1:解分式方程. ★★ 填空题、解答题
考点2:分式方程的实际应用. ★★★★ 选择题、解答题
考点2 分式方程的实际应用
典例6 [嘉兴中考] 为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为
A.
B
解析:∵荧光棒的单价为
根据题意,得
典例7 [湖州中考] 某企业承接了27 000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产.
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
解:(1)设甲车间有
由题意,得
解得
答:甲车间有30名工人参与生产,乙车间有20名工人参与生产.
①求乙车间需临时招聘的工人数.
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1 500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
(2)①设方案二中乙车间需临时招聘
由题意,得
经检验,
∴乙车间需临时招聘5名工人.
②企业完成生产任务所需的时间为
∴选择方案一需增加的费用为
选择方案二需增加的费用为
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
